微分方程式で数学モデルを作ろう１

• モデルを作るために、変数にするものの定義を明快にする
• モデルを拡張するとき
  • 変数が増える
  • 拡張される元のモデルは、拡張されたモデルの特別な条件を満足する場合。その条件とは？
• 指数関数ってなんだっけ？
  • 指数関数
  • 指数的増加
• こちらとこちらから
• Rのode()を使ってみる

• • 縦軸を対数にすると、指数増加は直線

# package をインストールする
install.packages("deSolve")
# packageを読み込む
library(deSolve)
# 微分方程式を表す関数を作る
# ode()関数に渡す微分方程式を表す関数は、変数tと従属変数yと係数のベクトルとを順番に渡す
my.func1<-function(t,y,pars){
# 返り値はリストで返す
# dy/dt = pars[1] y という微分方程式
	list(pars[1]*y)
}
my.func2<-function(t,y,pars){
# dy/dt = pars[1] y(1-y/pars[2]) という微分方程式
	list(pars[1]*y*(1-y/pars[2]))
}
# やってみる
# 係数を作る
a<-2
b<-3
pars1<-c(a)
pars2<-c(a,b)
# yの初期値を決める
y<-1
# 計算する時刻ポイントを決める
times<-seq(from=0,to=1,length=100)
# ode()関数に処理させる
out1<-ode(y = y, times = times, func = my.func1,pars1)
out2<-ode(y = y, times = times, func = my.func2,pars2)
# 出力は２列の行列で、第１列が時刻、第２列がyの計算結果値
# ２つのカーブを重ねて描く
# ２つのカーブのy軸をそろえる
ylim<-range(c(out1[,2],out2[,2]))
# 第１カーブを描いて
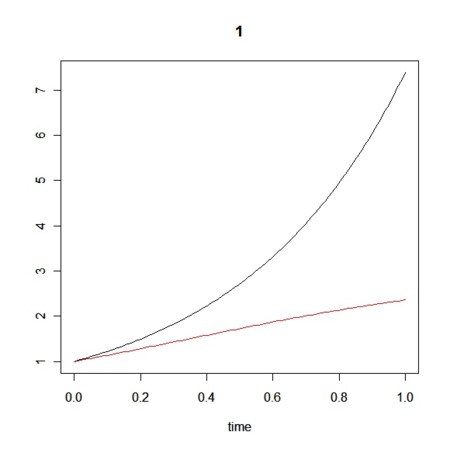
plot(out1,ylim=ylim)
# 重ね描き指定をして
par(new=TRUE)
# 第２カーブを描く
plot(out2,col=2,ylim=ylim)

# 次にyを対数にして描きなおす
# ここで小休止(指示があるまで次を描かないようにする)
par(ask=TRUE)
# y軸範囲を与えなおす
ylim2<-log(range(c(out1[,2],out2[,2])))
# ２カーブを描く。こちらでは、指数的増加は直線
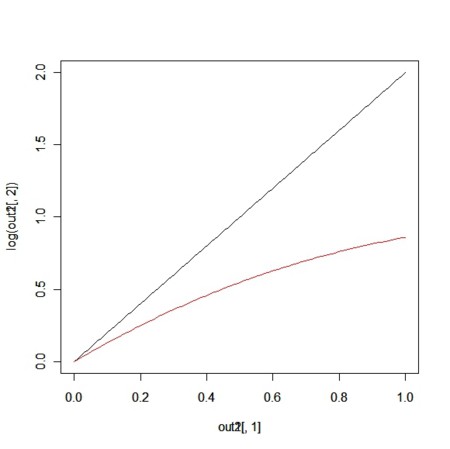
plot(out1[,1],log(out1[,2]),ylim=ylim2,type="l")
par(ask=FALSE)
par(new=TRUE)
plot(out2[,1],log(out2[,2]),col=2,ylim=ylim2,type="l")