```{r,echo=FALSE}
nI<-4 # 虚数固有値数
# 虚数とその共役複素数(である虚数)との固有値
Ss<-complex(real=rep(0,nI),imaginary=rnorm(nI))
Ss <- c(Ss,Conj(Ss))
n<-length(Ss)
S<-matrix(0,n,n)
for(i in 1:nI){
st<-(i-1)*2+1
S[st,st]<-Re(Ss[i])
S[st,st+1]<--Im(Ss[i])
S[st+1,st]<-Im(Ss[i])
S[st+1,st+1]<-Re(Ss[i])
}
library(GPArotation)
# 適当な正方行列とその逆行列
V2<-matrix(rnorm(n^2),n,n)
U2<-solve(V2)
A<-V2%*%S%*%U2
eigen.out<-eigen(A)
V<-eigen.out[[2]]
U<-solve(V)
B<-diag(eigen.out[[1]])
x<-seq(from=0,to=10,length=101)
# 要素の初期値ベクトルとその経過記録行列
Ys<-matrix(0,length(x),n)
Ys0<-runif(n)
Ys0<-rep(0,n)
Ys0[1]<-1
IMS<-rep(0,length(x))
for(i in 1:(length(x))){
Bex<-diag(exp(eigen.out[[1]]*x[i]))
Aex<-V%*%Bex%*%U
Ys[i,]<-Aex%*%Ys0
ims<-sum(Im(Ys[i,])^2)
IMS[i]<-ims
#if(ims>0.000001)print(ims)
}
matplot(Re(Ys),type="l",xlab="time")
```
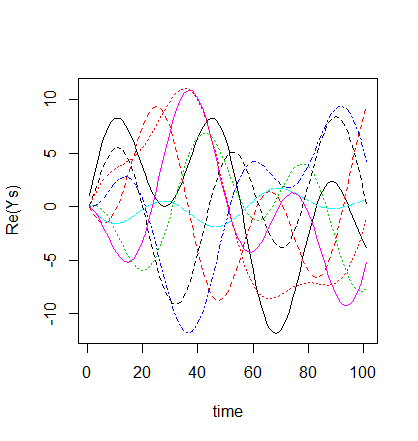
生命現象では、このようにいくつかの要素が減ったり増えたりしています。
これらの現象のメカニズムを明らかにしたいわけですが、どのような背景が読み取れるでしょうか?
そのための道具についての章です。
三角関数は次のように書き表します。
$$
\begin{equation*}
x = \cos{t}\\
y = \sin{t}
\end{equation*}
$$
グラフを描いてみることにします。
データを扱うフリーソフトR("あーる")を使って、作図してみます。
Rのダウンロードは簡単です。http://cran.r-project.org/ このサイトから、コンピュータのOSに合わせてダウンロードして指示に従ってクリックするだけ。ウイルスなど危ないこともありません。
```{r}
L <- 2*pi*3
# 0から1までに1000個の等間隔値を作成しそのすべてをL倍する
t <- seq(from=0,to=1,length=1000)*L
# x,yの座標を三角関数で産出する
x <- cos(t)
y <- sin(t)
# 横軸にt、縦軸にxで、色を虹色に変えながらプロットする
plot(t,x,pch=15,cex=0.5,col=rainbow(100))
# yを同様に色を1(黒)で線状(type="l"ine)に引く
points(t,y,pch=15,cex=0.5,col=1,type="l")
```
xが減るとそれを追いかけるようにしてyも減り、xが増えるとyも後を追う、というように見ることができる。
yが大きい時、xは小さくなり、yが小さい時、xは大きくなる
xが大きい時、yは大きくなり、xが小さい時、yは小さくなる、
とも見える。
yの値とxの増減(微分)、xの値とyの増減(微分)との間の関係を言葉で表したものであって、数式では以下のようになる。
$$
\begin{equation}
\frac{dx}{dt} = \frac{d}{dt}\cos{t} = - \sin{t} = -y\\
\frac{dy}{dt} = \frac{d}{dt}\sin{t} = \cos{t} = x
\end{equation}
$$
2つの要素が相互に働きかける関係が三角関数として表現され、2行の微分方程式(連立微分方程式)になっていました。
三角関数は「負の値」を取りますが、自然界ではすべてのものが「正の値」になることも多いです。したがって、生命現象で登場する2要素の連立微分方程式はちょっと複雑になります。
まずグラフを描いてみます。
```{r}
alpha <- 0.2
beta <- 0.00002
gamma <- 0.2
delta <- 0.000014
x1 <- 10000
y1 <- 500
n.iter <- 30000
x <- y <- rep(0,n.iter)
dt <- 0.01
x[1] <- x1
y[1] <- y1
for(i in 2:n.iter){
x[i] <- x[i-1] + (alpha*x[i-1] - beta*x[i-1]*y[i-1]) * dt
y[i] <- y[i-1] + (delta*x[i-1]*y[i-1] - gamma*y[i-1]) * dt
}
s <- which(x>0 & y>0)
matplot(cbind(x[s],y[s]),type="l")
```
三角関数のように左右対称・上下対称からはかなりずれています。しかしながら、x,yが追いかけっこをしている点は同じです。
これがどのような因果関係になっているかは、対応する微分方程式を見ることで明快になります。
$$
\begin{equation}
\frac{dx}{dt} = \alpha x - \beta xy\\
\frac{dy}{dt} = -\gamma y + \delta xy\\
\alpha, \beta, \gamma, \delta > 0
\end{equation}
$$
+ xの増減は、2つの要素の和からなっており
+ xの量に比例して増加量が増える
+ xとyの積に比例して減少量が増える
+ yの増減は、2つの要素の和からなっており
+ yの量に比例して減少量が増える
+ xとyの積に比例して増加量が増える
と読めます。
> 生態系で放っておくと繁殖するが、草食動物xが肉食動物yに出会う(x,yの積)と捕食され、肉食動物yは放っておくと減るが、草食動物xに出会うと繁殖する
という場合がこのようなパターンになります。
x,yを化学分子とみなせば、放っておくと増える分子xはyと反応して減少し、yは放っておくと消失するが、xと反応することで増加する、というようなパターンがこれに相当します。
上の例では、2要素が相互に影響しあうことで周期的な変化が現れました。
2要素が反応しながら、かつ、ある空間を拡散していくと、微分方程式自体は単純ながら、複雑な様子模様が現れます。
動物の体表の模様の形成などの原理の1つにこの反応拡散系があります。
偏微分の記号、空間積分の記号など見慣れないものがあるかも知れませんが、記号だと割り切ることも「数理生物学」のしきたりと思えば、今は気にする必要はありません。
第1項は指定した拡散係数による拡散を表し、第2・第3項がu,vの相互作用・反応を表しています。uの減少とvの増加とが、係数F,kを介して連結しており、反応の速さはu,vの濃度の両方とに依存しています。
$$
\begin{equation}
\frac{\partial u}{\partial t} = d_u \nabla^2 u -uv^2 +F(1-u)\\
\frac{\partial v}{dt} = d_v \nabla^2 v + uv^2 - (F+k)v
\end{equation}
$$
```{r}
# 時間経過
Niter<-100
# Space
X<-100
# 2種の濃度分布行列
U<-V<-matrix(0,X,X)
# 初期濃度分布設定
a<-X*0.3
U[a,a]<-1
V[a,a]<-0
U[X-a,X-a]<-0
V[X-a,X-a]<-1
U<-matrix(runif(X^2),X,X)
V<--U+1
# 反応を定める係数
F<-0.5
k<-0.1
# 拡散係数
dif1<-0.3 # Du
dif2<-0.4 # Dv
files <- list()
cnt <- 1
for(i in 1:Niter){
tmpU<-tmpV<-matrix(0,X,X)
for(j1 in 1:X){
for(j2 in 1:X){
tmpU[j1,j2]<--U[j1,j2]*V[j1,j2]^2+F*(1-U[j1,j2])
tmpV[j1,j2]<-U[j1,j2]*V[j1,j2]^2-(F+k)*V[j1,j2]
}
}
U<-U+tmpU
V<-V+tmpV
tmpU<-tmpV<-matrix(0,X,X)
for(j1 in 2:(X-1)){
for(j2 in 2:(X-2)){
tmpU[j1,j2]<-dif1*(U[j1,j2+1]+U[j1,j2-1]+U[j1+1,j2]+U[j1-1,j2]-4*U[j1,j2])
tmpV[j1,j2]<-dif2*(V[j1,j2+1]+V[j1,j2-1]+V[j1+1,j2]+V[j1-1,j2]-4*V[j1,j2])
}
}
U<-U+tmpU
V<-V+tmpV
if(i%%10==0){
files[[cnt]] <- U
cnt <- cnt+1
}
}
par(mfrow=c(3,3))
for(i in 1:9){
image(files[[i]],breaks=seq(from=0,to=1,by=0.1),col=terrain.colors(10))
}
par(mfrow=c(1,1))
```
別のやり方でグラフを描きます。
円が描かれます。
三角関数は次のように円を表している。
```{r}
plot(cos(t),sin(t),pch=15,cex=0.5,col=rainbow(100))
```
生態系・分子反応系の追いかけっこを同様に表すと「円」ではないが、周回軌道を描きます。
```{r}
plot(x,y,pch=15,cex=0.5,col=rainbow(100))
```
これらの軌道は、ぐるりと回って元の位置に戻り、また同じ軌道をたどっており、周回軌道となっています。
生命体の状態を捉えるときに、いろいろな分子の量の変化で捉える場合を考えてみます。生命体は、刻一刻と変化してはいますから、いろいろな分子の量は絶えず変化していますが、長い目で見ると安定しています。
仮に、2分子の量に着目すれば、上の図のように2次元平面に周回軌道を描きます。
3分子の場合をグラフにしてみます。
3分子の量の時間変化をグラフにすれば、3本のカーブになりますし、それを3次元空間の軌道として描くこともできます。
```{r}
library(rgl)
```
```{r setup}
knit_hooks$set(rgl = hook_rgl)
q1 <- 1
q2 <- 20
r1 <- 1
r2 <- 0.3
t <- seq(from=0,to=1,length=1000)*30
x <- r1 * cos(q1*t) + r2 * cos(q2*t)*cos(q1*t)
y <- r1 * sin(q1*t) + r2 * cos(q2*t)*sin(q1*t)
z <- r2 * sin(q2*t)
matplot(cbind(x,y,z),type="l")
```
ガタガタしていてさほど美しい仕組みに見えないかもしれませんが、以下のように3次元空間の軌跡にすると印象が変わるかもしれません。
```{r, rgl=TRUE}
xyz <- cbind(x,y,z)
xyz <- rbind(xyz,rep(max(xyz),3))
xyz <- rbind(xyz,rep(min(xyz),3))
view3d(theta = -30, phi = 60)
plot3d(xyz)
```
この形はドーナツ型・トーラスですが、2つの円軌道の組み合わせで出来ています。
このように状態を空間上の点とみなし、時間変化を空間上の曲線とみなす考え方を状態空間モデルと呼びます。
状態空間モデルでは、空間にどのような曲線が描かれるかに興味があります。
また、ものごとを観察すると空間上の点としてとらえることができますが、そのデータから、どのような軌道が存在しているのか、その軌道を決めているルール(微分方程式)はどんなものかを明らかにすることが、生命現象の理解の目標となります。
医学で言えば、「健康である」という定常状態〜周回軌道と「病気である」という定常状態〜周回軌道とがあって、何かの拍子に「健康周回軌道」から「病気周回軌道」に飛び移ってしまうことが「発病」となります。このモデルでは、何が「飛び移り」を起こすのか、「健康周回軌道」に戻るための医療介入とは何なのか、ということを状態空間上の要因として検討することが可能となります。
※ ここまで読んできたあなたはそれなりに数理生物学が好きなはずです。統計遺伝学分野の教員 山田 は医学部医学数学研究会(MIKU)の顧問をしています。数学に関することをネタに雑談する部です。興味があれば部員もしくは山田まで、お気軽にご連絡ください。
三角関数は$x=\cos(t),y=\sin(t)$円を描いていぐるぐる回ります。
x軸を実数直線、y軸を虚数直線とすると、
$$
\begin{equation}
(x,y) = (\cos(t),\sin(t))
\end{equation}
$$
という2次元座標は、複素数
$$
\begin{equation}
\cos{t} + i \sin{t}
\end{equation}
$$
に対応します。
$$
\begin{equation}
\cos{t} + i \sin{t} =e^{i t}
\end{equation}
$$
とも書きます。
もう一度$x=\cos(t)$に戻って考えます。
xは増えたり減ったりする関数ですが、これは
$$
\begin{equation}
z = e^{i t}
\end{equation}
$$
の実数部分だけを見ているとも考えられます。
さて、力学系・微分方程式の観点から、指数関数は特殊な関数です。
$$
\begin{equation}
\frac{d}{dt}e^{kt} = k e^{kt}
\end{equation}
$$
という簡単な式になります。
定数と自身だけで完結している微分方程式です。
```{r}
par(mfcol=c(1,3))
k <- 1
plot(t,exp(k*t),type="l",main="k>0")
k <- -1
plot(t,exp(k*t),type="l",main="k<0")
k <- 0
plot(t,exp(k*t),type="l",main="k=0")
par(mfcol=c(1,1))
```
それぞれ、
指数関数的増加、指数関数的減少、一定、という変化様式に相当します。
指数関数的増加は、細菌が倍々に増えていくときなどに相当しますし、指数関数的減少は、一定の割合で死亡者が出るときの生存者の変化になどに相当します。
このようにありふれた変化が指数関数です。
なぜありふれているかと言えば、生物の現象においては、支配しているルールが単純な現象が多いことの裏返しとも言えるでしょう。
さて、三角関数に話を戻します。
三角関数$x=\cos(t)$は、$z=e^{it}=\cos(t) + i \sin(t)$の実数部分だけを見ていると書きました。
ということは、三角関数として見える、周期的な増減変化というのは、指数関数が持つ単純な微分方程式で考えれば
$$
\begin{equation}
\frac{d}{dt} e^{(a+ib) t} = (a+ib)e^{(a+ib)t}
\end{equation}
$$
としたときに$a+ib$の$a=0,b=1$の場合に相当するらしいことがわかります。
逆に指数関数的増加というのは、$a>0,b=0$の場合であり、指数関数的減少というのは$a<0,b=0$であって、無変化は$a=0,b=0$の様です。
では色々な$(a,b)$について「指数関数的変化」をグラフにしてみます。
虚部の存在が振動を表し、実部が全体としての増減を決めることがわかります。
```{r}
t <- seq(from=0,to=1,length=1000)*10
par(mfrow=c(2,2))
a <- 0; b<- 0
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Constant")
a <- 1; b<- 0
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Monotone-Incr")
a <- -1; b<- 0
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Monotone-Decr")
a <- 0; b<- 1
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Periodic")
a <- 0; b<- 3
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="High-freq")
a <- 0.3; b<- 10
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Periodic-Incr")
a <- -0.3; b<- 10
plot(Re(exp(complex(real=a,imaginary=b)*t)),type="l",main="Periodic-Decr")
par(mfrow=c(1,1))
```
三角関数の「全体として不変」で「振動する」という性質は、微分方程式・指数関数に照らして複素数に対応付けたとき、「実部が0」で「虚部が非0」であるということを意味していることが解ります。
1変数の微分方程式
$$
\begin{equation}
\frac{dx}{dt} = ax
\end{equation}
$$
のときに
$$
\begin{equation}
x = K e^{at}
\end{equation}
$$
となる話があり、aが複素数でもよいこと、aの実部が0のときに発散も収束もせず、虚部がある場合には周期変動をすることが示されました。
では、これが連立微分方程式に拡張されるとどうなるのでしょうか。
複数の因子が相互に影響を及ぼしあいながら、全体としては発散も収束もせずに周期変化をするような現象の記述についての話になります。
x,yの追いかけっこ
$$
\begin{equation}
\frac{dx}{dt} = \frac{d}{dt}\cos{t} = - \sin{t} = -y\\
\frac{dy}{dt} = \frac{d}{dt}\sin{t} = \cos{t} = x
\end{equation}
$$
に話を戻します。
このx,yが満足する連立微分方程式は、三角関数を使わずに、行列を使うことで次のように表せます。
$$
\begin{equation}
\begin{pmatrix}\frac{dx}{dt}\\ \frac{dy}{dt}\end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}
\end{equation}
$$
$(x,y)$を$(x_1,x_2)$と書き直せば、
$$
\begin{equation}
\begin{pmatrix}\frac{dx_1}{dt}\\ \frac{dx_2}{dt}\end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\\
\frac{d\mathbf{x}}{dt} = \mathbf{Zx}\\
\end{equation}
$$
と次のベクトルと行列とを使って簡単に表すことができます。
$$
\begin{equation}
\mathbf{x} = \begin{pmatrix}x_1 \\ x_2 \end{pmatrix}\\
\mathbf{Z} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}
\end{equation}
$$
$\mathbf{x},\mathbf{Z}$と太字なのは、それぞれ、ベクトル(多変数)、行列であることを意味しています。
次の2式を比べます。
$$
\begin{equation}
\frac{dx}{dt} = z x\\
\frac{d\mathbf{x}}{dt} = \mathbf{Zx}
\end{equation}
$$
上式のxが発散も収束もしないで周期的変化をするときには、zが純虚数であるのでした。
下式の$\mathbf{x}=(x_1,x_2)$がいずれも、発散も収束もしないときにもこれと似たような制約があります。
その制約には再び純虚数が登場します。
その制約を具体例に沿ってみてみます。
$$
\begin{equation}
\mathbf{Z} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{-i}{\sqrt{2}} & \frac{i}{\sqrt{2}} \end{pmatrix}\begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\
\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{-i}{\sqrt{2}} \end{pmatrix}
\end{equation}
$$
このように3つの行列の積にします。
この3つの行列の特徴を以下に説明します。
$$
\begin{equation}
\mathbf{Z} = \mathbf{V S U}\\
\mathbf{V} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{-i}{\sqrt{2}} & \frac{i}{\sqrt{2}} \end{pmatrix}\\
\mathbf{S} = \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\\
\mathbf{U} = \mathbf{V}^{-1} = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{-i}{\sqrt{2}} \end{pmatrix}
\end{equation}
$$
$\mathbf{V}$と$\mathbf{U}$とは相互に逆行列の関係にあり、
$$
\begin{equation}
\mathbf{VU} = \mathbf{UV} = \mathbf{E} : \text{単位行列}
\end{equation}
$$
中央の行列$\mathbf{S}$は対角成分以外は0であり、対角行列と呼ばれます。また、このような対角成分は行列$\mathbf{z}$の固有値と呼ばれます。
今の場合、2つの固有値は
$$
\begin{equation}
i = \cos(\frac{\pi}{2}) + i \sin(\frac{\pi}{2})=e^{0 + i\frac{\pi}{2}}\\
-i = \cos(\frac{3\pi}{2}) + i \sin(\frac{3\pi}{2})=e^{0 +i \frac{3\pi}{2}}
\end{equation}
$$
と表すことができて、$e^{a+bi}$として表した場合、どちらも$a=0$と指数が純虚数となっています。
ちなみに
$$
\begin{equation}
e^{bi}= \cos{b} + i \sin{b}
\end{equation}
$$
なので、結局、$\mathbf{Z}$の固有値は絶対値が1の複素数になっていました。
このようなとき、つまり絶対値が1の複素数と書き表せるとき、$\mathbf{z}$のすべては発散も収束もしないで増減しながら変動します。
なぜなら
$$
\begin{equation}
A^t = (VSV^{-1})^t = VS(V^{-1}V)S(V^{-1}V)...(V^{-1}V)S(V^{-1})==V SESE...ESV^{-1}=V (S^t) V^{-1}
\end{equation}
$$
がtが整数であるか実数であるかによらず成り立つようにできますが、そのとき、$S^t$は$S$の対角成分$s_i$のそれぞれを$s_i^t$としてそれを対角成分とした行列にまります。このような時刻tに対応する対角行列の対角成分は$s_i = e^{bi}$のとき、変動はするけれども発散も収束もしないからです。
これは、$\mathbf{z}$の変数の数が1のときの拡張になっていることがわかります。
この例はごく単純でしたが、冒頭の8要素の周期変動のグラフはこれを背景にして作成したものです。
こんな例を試してみます。
$$
\begin{equation}
\frac{dx_1}{dt} = -x_2\\
\frac{dx_2}{dt} = -x_3\\
\frac{dx_3}{dt} = -x_4\\
\frac{dx_4}{dt} = x_1
\end{equation}
$$
$$
\begin{equation}
\begin{pmatrix}\frac{d x_1}{dt} \\ \frac{d x_2}{dt} \\ \frac{d x_3}{dt} \\ \frac{d x_4}{dt} \end{pmatrix} = \begin{pmatrix}0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}
\end{equation}
$$
このような行列
```{r}
A <- matrix(c(0,-1,0,0,0,0,-1,0,0,0,0,-1,1,0,0,0),byrow=TRUE,4,4)
eigen.out <- eigen(A)
V <- eigen.out[[2]]
U <- solve(V)
s <- eigen.out[[1]]
t <- seq(from=0,to=1,length=1000)*10
X <- matrix(0,length(t),4)
x1 <- c(1,3,10,100)
for(i in 1:length(t)){
X[i,] <- V %*% diag(s^t[i]) %*% U %*% x1
}
matplot(Re(X),type="l")
```
対角行列はどうなっているかというと
```{r}
diag(s)
```
のように、複素数になっています。この複素数の絶対値はここでは確かめませんが1になっています。
複数の因子が相互に影響しあいながら、変動し周期的に変化する現象の基本には、三角関数があり、それが周期性をもたらすことを理解するには、指数関数と複素数を解に持つ微分方程式が登場しました。
また、連立方程式には行列計算も登場し、行列には固有値やそれを用いた行列の分解などが役に立つこともわかりました。
