Permutohedron ４度

• こちらでPermutohedronのことを書いている
• N=3の場合は、６つの順列であって、それを３次元空間に均等配置すると、正八面体であると書いた
• さて、正八面体の１２本の辺のうち、どれに線を引くのがよいのだろうか？
• (1,2,3)の３数のうち、２数を取り出して、入れ替えた並べ方は(1,3,2),(2,1,3),(3,2,1)の３通りだから、この３つと隣り合わせたい(隣り合わせには辺を引く)
• 引いてみよう

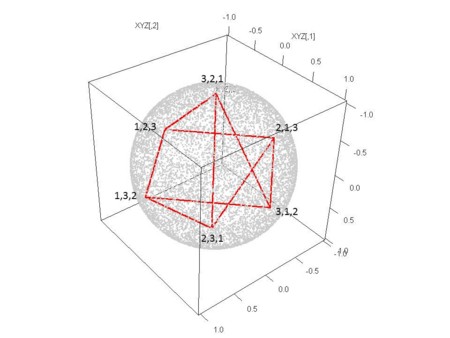
• 頂点数6
• 辺数8
• サイクルが四角形を作っていて、それは４個
• 球の大円上の正方形があって、その大円を赤道としたときの北極南極に残りの２頂点が取ってあると見たときに、赤道上の正方形に対応する辺を引き、南北極を結ぶ線を引き、南極から赤道上の２点(経度上１８０度離れている)に辺を引き、北極からは、南極から辺の引かれていない赤道上の２点に辺を引いてある

Vs<-matrix(
c(
1,0,0,
0,1,0,
0,-1,0,
0,0,1,
-1,0,0,
0,0,-1
),
6,3,
byrow=TRUE
)

library(gtools)
perms<-permutations(3,3)

Ne<-101
t<-seq(from=0,to=1,length=Ne)
Es<-NULL
for(i in 1:(length(Vs[,1])-1)){
	for(j in (i+1):length(Vs[,1])){
		if(prod(perms[i,]-perms[j,])==0){
			tmp<-matrix(0,length(t),3)
			for(k in 1:length(t)){
				tmp[k,]<-Vs[i,]*t[k]+Vs[j,]*(1-t[k])
			}
			Es<-rbind(Es,tmp)
		}
		
	}
}

NptE<-length(Es[,1])

Npt<-10000
sp<-matrix(rnorm(Npt*3),Npt,3)
sp<-sp/sqrt(apply(sp^2,1,sum))

XYZ<-rbind(sp,Es)
col<-c(rep(gray(8/10),Npt),rep(2,NptE))

library(rgl)
plot3d(XYZ,col=col)