2014-11-14

三角メッシュの球面埋め込み

平面グラフは、平面座標上に描ける
三角メッシュは３次元物体の表面をTriangulationしたものなので、その３次元表面が連続ならば、それは平面グラフになる。したがって、その表面は平面に写せる
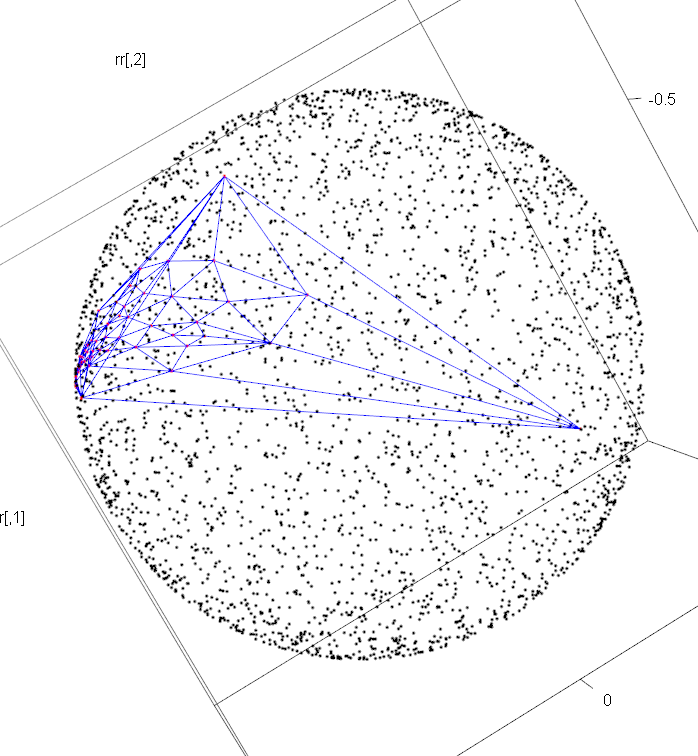
平面座標は球面座標に変換できる
したがって、３次元物体の表面は、Triangulation -> planar graph -> 平面座標 -> 球面座標として、球面に持ち込める
その一つの方法をやってみる
また、三角メッシュが、辺縁のない物体表面のときに、一つの三角形を指定して、それを辺縁と見立てることで上記の手続きに持ち込めるので、今回は、周縁が三角形になっている平面グラフを考えよう
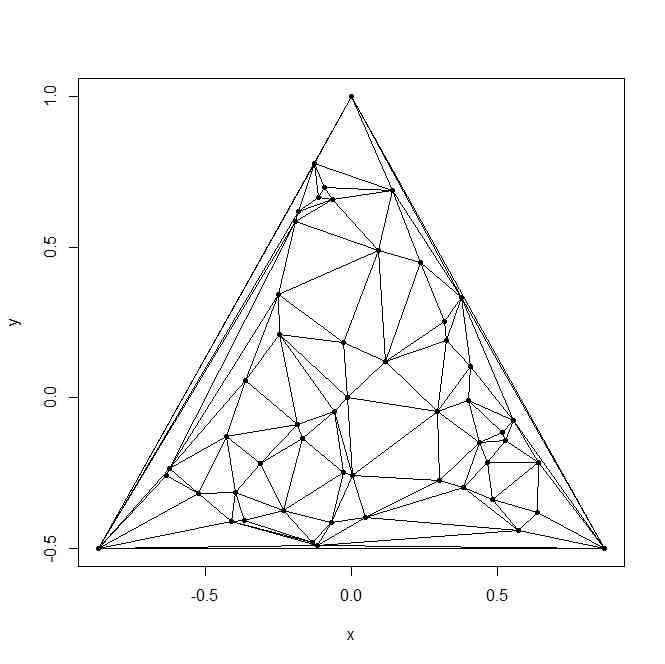
まず周縁が三角形である平面グラフを作る
- 三角形を作り、その内部点を $a_1 v_1 + a_2 v_2 + a_3 v_3; a_1+a_2+a_3=1,a_i > 0$ とすることで発生し、それにTriangulationする

# 正三角形の３点を決める
L <- 1
x <- c(L*sqrt(3)/2,0,-L*sqrt(3)/2)
y <- c(-L/2,L,-L/2)
# dirichlet乱数を用いて、内部点の係数を作る
library(MCMCpack)
n <- 50
R <- rdirichlet(n,rep(0.9,3))
xy <- cbind(x,y)
# 内部店座標を計算する
X <- R %*% xy
# 外縁３点と内部点とを合わせる
X <- rbind(xy,X)
# Triangulationする
library(geometry)
tri <- delaunayn(X) # ドロネー
# 三角形の頂点番号のリストからエッジリストを作る
el <- rbind(tri[,c(1,2)],tri[,c(2,3)],tri[,c(3,1)])
# グラフオブジェクトにして、そのりんせつ行列を取り出す
tmp.g <- graph.edgelist(el)
ad.m <- get.adjacency(tmp.g,sparse=FALSE)

# 辺の重みを1に変換する
ad.m <- ad.m + t(ad.m)
ad.m <- sign(ad.m)
# 対角成分を0にする
diag(ad.m) <- 0

plot(X,pch=20)
segments(X[el[,1],1],X[el[,1],2],X[el[,2],1],X[el[,2],2])

昨日の記事でやった、「共形変換を３次元で」をこの平面グラフに施して、立体的にする

my.conformal.3d <- function(X,As){
	X2 <- matrix(0,length(X[,1]),length(X[1,]))
	for(i in 1:2){
		for(j in (i+1):3){
			tmp <- X[,c(i,j)]
			as <- As[[i]][[j]]
			tmp.z <- tmp[,1]+tmp[,2]*1i
			tmp.z2 <- as[1]
			for(k in 2:length(as)){
				tmp.z2 <- tmp.z2 + as[k] * tmp.z^k
			}
			X2[,c(i,j)] <- X2[,c(i,j)] + cbind(Re(tmp.z2),Im(tmp.z2)) - X[,c(i,j)]
		}
	}
	X2 + X
}
As <- list()
As[[1]] <- list()
As[[1]][[2]] <- runif(3)*0.2 + 1i * runif(3)*0.1
As[[1]][[3]] <- runif(3)*0.1 + 1i * runif(3)*0.1
As[[2]] <- list()
As[[2]][[3]] <- runif(3)*0.1 + 1i * runif(3)*0.1

#X <- cbind(x,y,rep(0,length(x)))
XX <- cbind(X,rep(0,length(X[,1])))
X.out <- my.conformal.3d(XX,As)

plot3d(X.out)

for(i in 1:length(el[,1])){
segments3d(matrix(c(X.out[el[i,1],],X.out[el[i,2],]),nrow=2,byrow=TRUE))

}

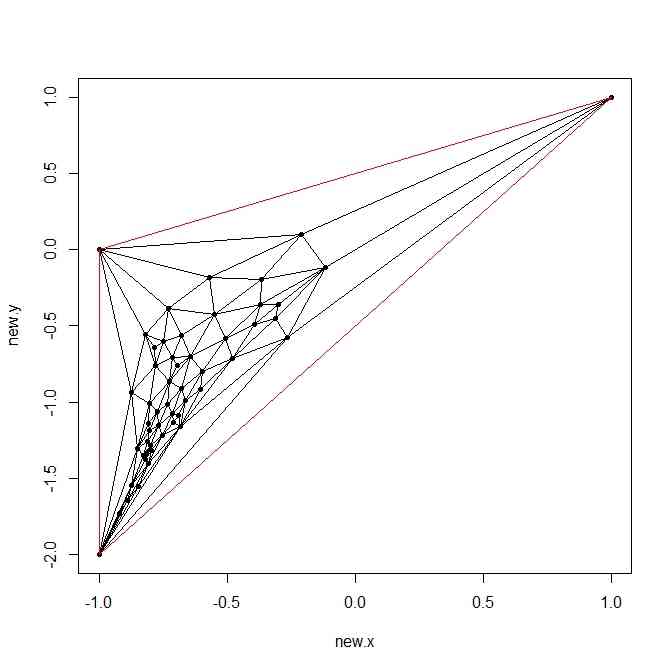
こんな立体表面の三角メッシュデータがあったときに、それをうまく平面におさめ、それを球面に乗せよう、という話
- ここでの課題は、三角メッシュデータには各点の３次元座標があるが、それはひとまず気にせず(使わず)、それがplanar graphであるという『教え』を信じて、平面座標を与えて、うまくplanarに描くという課題である
これをするのに、先ほど三角形の内部点の座標を与えた方法を使う
ある点が、ある点の集合が張る部分空間上にあるとき、張っている点に係数を与えて、その和が1になるようにするとよい
さらに、張っている点が凸包であるときにその内部点である、というのは、係数のすべてが正であるであるようにするとよい
今、外周の点と内部の点の位置ベクトルは、相互の連結関係から、 $v_i = \sum_{j} w_{ij} v_j;\sum_j w_{ij}=1$ と表せることになる
今、外周点については、座標を与えることとし、外周点間を結ぶエッジは無視することにし、外周点と連結な内部点については、その間を結ぶエッジが必ず、外周点から内部点に向かうとする。また、外周点については、自身から自身へのエッジがあるものとすると
- $M v = v$ という連立方程式ができる(ただし実際の連立方程式は、２次元の各次元座標についてそれぞれ立つ)。ただし、Mはすべての点の数をnとしたときに、nxn行列であって、この行列は、外周点を行の上を占めるようにすれば、行列の外周点に相当する行の部分は単位行列、それ以下の行については、このグラフの隣接行列のようになっていて、ただし、エッジには重みがあり、各行の和が1になるようにしたものになっている
- さて、この $M v = v$ のうち、上位の外周点分の行は $v_i=v_i$ という恒等式になっているので、不要。不要な行を除いた行列を $M'$ とする。
- また、外周点の座標はわかっているので、vも上位数行は定数である。定数部分を除いたものをv'とする。
- その定数に対応して、外周点と連結な点については、その寄与分が定数項としてあらわれるので $M' v' + V= v'$ というように表せる。ただしVは定数項を表すベクトル
- 右辺のv'を左辺に持ってくるということは、M'をM''=M'-I (Iは恒等行列)に替えればよいから
- 結局 $M'' v' = -V$ という連立方程式を解けばよい
- なお、ここでMのセルの値は、0または、正の数であって、各行の和が1という制約を満足すればなんでもよいこともわかる

# グラフの隣接行列
M <- ad.m
# 外縁３点の座標は与えるので以下のように。
M[1:3,] <- 0
M[1:3,1:3] <- diag(rep(1,3))
M
# 各行について寄与係数の輪を１にする
tmp <- apply(M,1,sum)
tmp.s <- which(tmp!=0)
M[tmp.s,] <- M[tmp.s,]/tmp[tmp.s]
M
# 座標を計算で求める対象だけに絞る
M. <- M[4:length(M[,1]),4:length(M[,1])]
# 対角成分を-1する
M.. <- M. - diag(rep(1,length(M.[,1])))
# 外縁３点の座標は適当に決めてよい
new.x.three <- matrix(c(1,1,-1,0,-1,-2),byrow=TRUE,ncol=2)
# 内部点の座標は不明だが、外縁由来分の計算のために仮に0と置く
new.x <- new.y <- rep(0,length(X[,1]))
new.x[1:3] <- new.x.three[,1]
new.y[1:3] <- new.x.three[,2]
# 外縁寄与分 V の計算
tmpx <- M %*% new.x
tmpy <- M %*% new.y
# 連立方程式を解く
tmp.new.x <- solve(M.., -tmpx[4:length(tmpx)])
tmp.new.y <- solve(M.., -tmpy[4:length(tmpy)])

new.x <- c(new.x[1:3],tmp.new.x)
new.y <- c(new.y[1:3],tmp.new.y)

new.X <- cbind(new.x,new.y)
plot(new.X,pch=20)
segments(new.X[el[,1],1],new.X[el[,1],2],new.X[el[,2],1],new.X[el[,2],2])

segments(new.X[1,1],new.X[1,2],new.X[2,1],new.X[2,2],col=2)
segments(new.X[2,1],new.X[2,2],new.X[3,1],new.X[3,2],col=2)
segments(new.X[3,1],new.X[3,2],new.X[1,1],new.X[1,2],col=2)

球面に乗せる

my.spherization <- function(X){
	z <- X[,1] + 1i*X[,2]
	L <- Mod(z)
	theta <- Arg(z)
	q <- 4*L/(L^2+4)
	w <- 2*L^2/(L^2+4)
	cbind(q*cos(theta),q*sin(theta),w-1)
}

new.sp.X <- my.spherization(new.X)

rr <- matrix(rnorm(3000*3),ncol=3)
rr <- rr/sqrt(apply(rr^2,1,sum))
plot3d(rr,col=1)

points3d(new.sp.X,col=2)
for(i in 1:length(el[,1])){
segments3d(matrix(c(new.sp.X[el[i,1],],new.sp.X[el[i,2],]),nrow=2,byrow=TRUE),col=4)

}