整理し直す：組み合わせの団代数、flag minor

• 資料はこちら:

https://arxiv.org/pdf/1005.1086.pdf

• 要素数nの集合の部分集合の族から全体と空集合を除くと、となり、その要素数は
• これのflag minorを考える
  • flag minorとは、行が、部分集合、列は、元の行列の左詰めの列になったような正方行列の行列式のこと
• 今、ととをFrozen とし、それ以外をMutableとする
• Frozenは常に現れ、Mutableは一部(個だけが現れるような箙をつくると
• Mutableのうちの１つを入れ替えて別のMutableに変異させることができる
• これをやるために、ちょっと工夫が必要で、１要素を加える。これはオリジナルの行列の行列式ではなくとないう特殊な形をしているが、それさえ許せば団代数になる
• Flag minorの間には、という関係がある
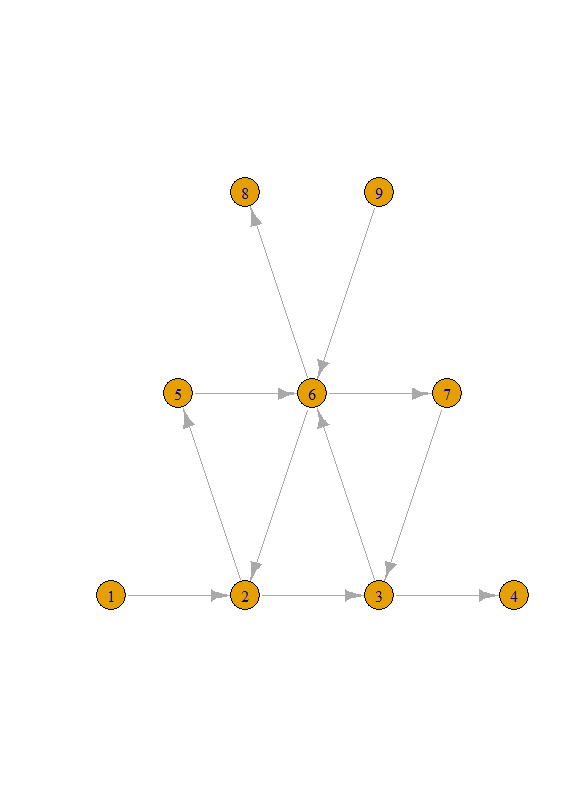
• 文章で書いてもわかりにくいので絵で描く

• Rで実験

library(igraph)
# Flag minor cluster algebra matrix

my.B.flagminor <- function(n){
	unbound.chamber <- 2 * (n-1)
	bound.chamber <- (n-1) * (n-2) /2
	total.chamber <- unbound.chamber + bound.chamber
	
	B <- matrix(0,total.chamber,total.chamber)
	
	n.chamber.per.row <- n:2
	n.row <- n-1
	
	id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
	
	# horizontal arrow
	for(i in 1:(n.row-1)){
		for(j in 1:(n.chamber.per.row[i]-1)){
			tmp <- id.first.row[i] + j -1
			tmp2 <- tmp + 1
			B[tmp,tmp2] <- 1
		}
	}
	# up row
	for(i in 1:(n.row-1)){
		for(j in 2:(n.chamber.per.row[i]-1)){
			tmp <- id.first.row[i] + j -1
			tmp2 <- id.first.row[i+1] + (j-1) -1
			B[tmp,tmp2] <- 1
		}
	}
	# down row
	for(i in 2:n.row){
		for(j in 2:n.chamber.per.row[i]){
			tmp <- id.first.row[i] + j -1
			tmp2 <- id.first.row[i-1] + j -1
			B[tmp,tmp2] <- 1
		}
	}
	#B.skew <- B - t(B)
	frozen <- c()
	for(i in 1:(n.row-1)){
		frozen <- c(frozen,id.first.row[i],id.first.row[i+1]-1)
	}
	frozen <- c(frozen,id.first.row[n.row],id.first.row[n.row]+1)
	mutable <- (1:length(B[,1])) [-frozen]
	B. <- B[c(mutable,frozen),c(mutable,frozen)]
	B.skew <- B. - t(B.)
	B.ext <- B.skew[,1:length(mutable)]
	return(list(B.ext = B.ext,B=B,B.skew=B.skew,B.=B.))
}

my.layout.flagminor <- function(n){
	unbound.chamber <- 2 * (n-1)
	bound.chamber <- (n-1) * (n-2) /2
	total.chamber <- unbound.chamber + bound.chamber
	
	n.chamber.per.row <- n:2
	n.row <- n-1
	
	id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
	xy <- matrix(0,0,2)
	for(i in 1:n.row){
		tmp <- cbind(1:n.chamber.per.row[i] + i * 0.5,rep(i,n.chamber.per.row[i]))
		xy <- rbind(xy,tmp)
	}
	#xy[length(xy[,1]),1] <- xy[length(xy[,1]),1] + 0.5
	
	return(xy)

}

my.B.mut <- function(B,k){
	new.B <- B
	n <- length(B[1,])
	m <- length(B[,1])
	rule1 <- FALSE
	for(i in 1:m){
		for(j in 1:n){
			if(i == k || j == k){
				rule1 <- TRUE
			}else{
				rule1 <- FALSE
			}
			if(rule1){
				new.B[i,j] <- -B[i,j]
			}else{
				new.B[i,j] <- B[i,j] + 1/2 * (abs(B[i,k]) * B[k,j] + B[i,k] * abs(B[k,j]))
			}
		}
	}
	return(new.B)
}

n <- 4
out <- my.B.flagminor(n)



g <- graph.adjacency(out$B)

lout <- my.layout.flagminor(n)
plot(g,layout = lout)
||< 
>|r|
M <- matrix(rnorm(4^2),4,4)

> M[3,1] * det(M[c(2,3,4),1:3])*det(M[c(1,2),1:2]) + M[2,1] * det(M[c(3,4),1:2])*det(M[1:3,1:3])
[1] -0.4221082
> (-M[1,1] * det(M[2:4,1:3]) + M[2,1] * det(M[c(1,3,4),1:3])) * det(M[c(2,3),1:2])
[1] -0.4221082
> M[2,1]*det(M[c(1,3,4),1:3])
[1] -0.2134941
> M[1,1] * det(M[c(2,3,4),1:3]) + (-M[1,1]*det(M[c(2,3,4),1:3]) + M[2,1] * det(M[c(1,3,4),1:3]))
[1] -0.2134941
> dOmega <- (-M[1,1]*det(M[c(2,3,4),1:3]) + M[2,1] * det(M[c(1,3,4),1:3]))
> det(M[c(1,3),1:2]) * dOmega
[1] -1.333752
> M[1,1]*det(M[c(3,4),1:2])*det(M[1:3,1:3]) + M[3,1] * det(M[1:2,1:2])*det(M[c(1,3,4),1:3])
[1] -1.333752

> B <- out$B.ext
> B
      [,1] [,2] [,3]
 [1,]    0    1   -1
 [2,]   -1    0    1
 [3,]    1   -1    0
 [4,]    1    0    0
 [5,]    0   -1    0
 [6,]   -1    0    1
 [7,]    0    1   -1
 [8,]    0    0   -1
 [9,]    0    0    1
> B2 <- my.B.mut(B,3)
> B2
      [,1] [,2] [,3]
 [1,]    0    0    1
 [2,]    0    0   -1
 [3,]   -1    1    0
 [4,]    1    0    0
 [5,]    0   -1    0
 [6,]    0    0   -1
 [7,]    0    0    1
 [8,]    0   -1    1
 [9,]    1    0   -1
> B3 <- my.B.mut(B2,1)
> B3
      [,1] [,2] [,3]
 [1,]    0    0   -1
 [2,]    0    0   -1
 [3,]    1    1    0
 [4,]   -1    0    1
 [5,]    0   -1    0
 [6,]    0    0   -1
 [7,]    0    0    1
 [8,]    0   -1    1
 [9,]   -1    0    0
> B4 <- my.B.mut(B3,3)
> B4
      [,1] [,2] [,3]
 [1,]    0    0    1
 [2,]    0    0    1
 [3,]   -1   -1    0
 [4,]    0    1   -1
 [5,]    0   -1    0
 [6,]    0    0    1
 [7,]    1    1   -1
 [8,]    1    0   -1
 [9,]   -1    0    0
> B5 <- my.B.mut(B4,2)
> B5
      [,1] [,2] [,3]
 [1,]    0    0    1
 [2,]    0    0   -1
 [3,]   -1    1    0
 [4,]    0   -1    0
 [5,]    0    1    0
 [6,]    0    0    1
 [7,]    1   -1    0
 [8,]    1    0   -1
 [9,]   -1    0    0

組合せ部分集合の族に見られる団代数

• 要素数nの集合の部分集合の族は個の部分集合からなり、それらの包含関係は超立方体の形をしたポセットになっている
• このポセットを無向グラフと見ると、n正則グラフになっている
• 見方を変える
• n本の紐を互いに１度ずつだけ交叉させて、紐の順序を1,2,3,...,nからn,n-1,...,2,1にするようなn本の紐の配置をすることとする
• 紐の両端には閉じていない部屋が(n-1)個ずつ、併せて2(n-1)できる(一番下と一番上は数えない)
• 紐で閉じた部屋は個できる
• 閉じた部屋も閉じない部屋も、その部屋の下にある紐の番号の集合でID付けをすることにする
• このn本の紐が作る部屋のパターンにつき次のルールで矢印をつける
• 同じ段にあるときは、左から右に矢印をつける
• 左斜め下、左斜め上にある部屋に矢印をつける
• 両端にある閉じていない部屋の間には矢印をつけない
• この有向グラフを箙と見ると、閉じた部屋が変異可能頂点、閉じていない部屋が変異できない頂点とした、団代数になるという
• また、この団変異によって、すべての部分集合が現れるという
• この団代数では、2(n-1)個のfrozen な頂点～変異できない頂点があり、個の変異可能な頂点ができるので、拡大skew-symmetric 行列が作れる。列で行の行列
• 2,3,6の頂点がmutable、それ以外がfrozen
• 以下の行列では、1,2,3行、1,2,3列が、頂点番号2,3,6に相当
• 4,5,6,7,8,9行が、頂点番号1,4,5,7,8,9に相当
• この変異により、flag minor ({2,4,5}が選ばれたときには、全体の行列の2,4,5行と1,2,3列とを抜き出した正方行列を考え、その行列式のこと)に関して、トレミーの定理が成り立つことから、すべてのflag minorsが正であることの判定が、個のflag minorsの正の確認で済むことが導ける

> out$B.ext
      [,1] [,2] [,3]
 [1,]    0    1   -1
 [2,]   -1    0    1
 [3,]    1   -1    0
 [4,]    1    0    0
 [5,]    0   -1    0
 [6,]   -1    0    1
 [7,]    0    1   -1
 [8,]    0    0   -1
 [9,]    0    0    1
> my.B.mut(out$B.ext,2)
      [,1] [,2] [,3]
 [1,]    0   -1    0
 [2,]    1    0   -1
 [3,]    0    1    0
 [4,]    1    0    0
 [5,]   -1    1    0
 [6,]   -1    0    1
 [7,]    0   -1    0
 [8,]    0    0   -1
 [9,]    0    0    1

# Flag minor cluster algebra matrix

my.B.flagminor <- function(n){
	unbound.chamber <- 2 * (n-1)
	bound.chamber <- (n-1) * (n-2) /2
	total.chamber <- unbound.chamber + bound.chamber
	
	B <- matrix(0,total.chamber,total.chamber)
	
	n.chamber.per.row <- n:2
	n.row <- n-1
	
	id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
	
	# horizontal arrow
	for(i in 1:(n.row-1)){
		for(j in 1:(n.chamber.per.row[i]-1)){
			tmp <- id.first.row[i] + j -1
			tmp2 <- tmp + 1
			B[tmp,tmp2] <- 1
		}
	}
	# up row
	for(i in 1:(n.row-1)){
		for(j in 2:(n.chamber.per.row[i]-1)){
			tmp <- id.first.row[i] + j -1
			tmp2 <- id.first.row[i+1] + (j-1) -1
			B[tmp,tmp2] <- 1
		}
	}
	# down row
	for(i in 2:n.row){
		for(j in 2:n.chamber.per.row[i]){
			tmp <- id.first.row[i] + j -1
			tmp2 <- id.first.row[i-1] + j -1
			B[tmp,tmp2] <- 1
		}
	}
	#B.skew <- B - t(B)
	frozen <- c()
	for(i in 1:(n.row-1)){
		frozen <- c(frozen,id.first.row[i],id.first.row[i+1]-1)
	}
	frozen <- c(frozen,id.first.row[n.row],id.first.row[n.row]+1)
	mutable <- (1:length(B[,1])) [-frozen]
	B. <- B[c(mutable,frozen),c(mutable,frozen)]
	B.skew <- B. - t(B.)
	B.ext <- B.skew[,1:length(mutable)]
	return(list(B.ext = B.ext,B=B,B.skew=B.skew,B.=B.))
}

my.layout.flagminor <- function(n){
	unbound.chamber <- 2 * (n-1)
	bound.chamber <- (n-1) * (n-2) /2
	total.chamber <- unbound.chamber + bound.chamber
	
	n.chamber.per.row <- n:2
	n.row <- n-1
	
	id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
	xy <- matrix(0,0,2)
	for(i in 1:n.row){
		tmp <- cbind(1:n.chamber.per.row[i] + i * 0.5,rep(i,n.chamber.per.row[i]))
		xy <- rbind(xy,tmp)
	}
	#xy[length(xy[,1]),1] <- xy[length(xy[,1]),1] + 0.5
	
	return(xy)

}

my.B.mut <- function(B,k){
	new.B <- B
	n <- length(B[1,])
	m <- length(B[,1])
	rule1 <- FALSE
	for(i in 1:m){
		for(j in 1:n){
			if(i == k || j == k){
				rule1 <- TRUE
			}else{
				rule1 <- FALSE
			}
			if(rule1){
				new.B[i,j] <- -B[i,j]
			}else{
				new.B[i,j] <- B[i,j] + 1/2 * (abs(B[i,k]) * B[k,j] + B[i,k] * abs(B[k,j]))
			}
		}
	}
	return(new.B)
}

n <- 4
out <- my.B.flagminor(n)

library(igraph)

g <- graph.adjacency(out$B)

lout <- my.layout.flagminor(n)
plot(g,layout = lout)

out$B.ext
my.B.mut(out$B.ext,2)

京大学部入試数学問題をRで解く2021

• 問題はこちら
• □１
  • 問１　３次元空間の３点が指定する平面に対称な点の座標を求める
  • だいたいこのくらいの値

> Q
[1] 1.4444444 0.5555556 1.2222222

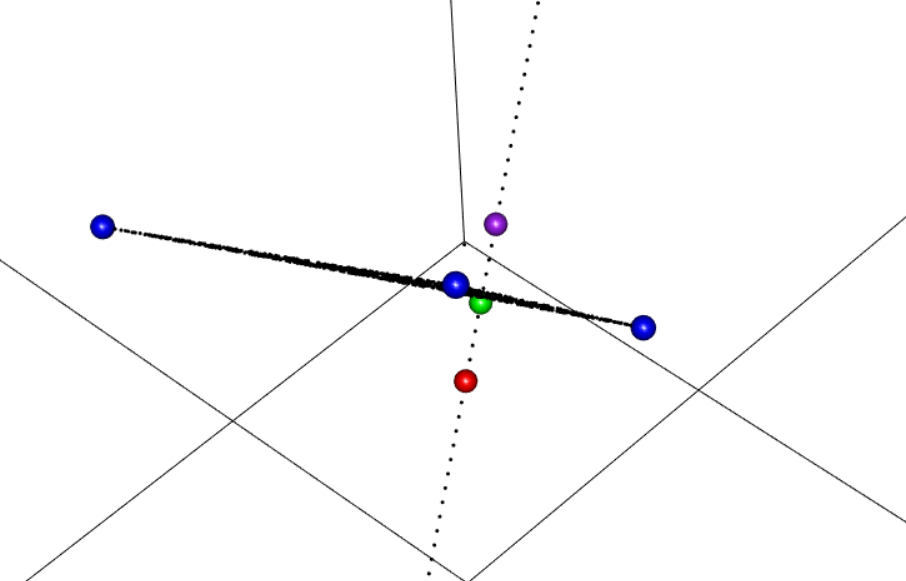
# 平面を指定する３点
A <- c(1,0,0)
B <- c(0,-1,0)
C <- c(0,0,2)

# ３角形の３辺ベクトル
AB <- B-A
AC <- C-A

# その法線方向ベクトル
n <- c(AB[2] * AC[3] - AB[3] * AC[2],AB[3] * AC[1] - AB[1] * AC[3], AB[1] * AC[2] - AB[2] * AC[1])

# ある点
P <- c(1,1,1)

# Pを通る直線をパラメタ表示するためのパラメタ
t <- seq(from=-3,to=3,length=100)
# 直線状の座標をたくさん発生させる
L <- matrix(0,length(t),3)
# Pを通り法線方向の点の座標を求める
for(i in 1:length(L[,1])){
	L[i,] <- P + t[i] * n/sqrt(sum(n^2))
}
# 3Dplot用パッケージ
library(rgl)
# ディリクレ乱数用パッケージ
library(MCMCpack)
# 三角形ABC内乱点発生用、ディリクレ乱数
S <- as.matrix(rdirichlet(1000,c(1,1,1))) 

# A,B,C,P,L,三角形ABC内乱点を３列行列にする
X <- rbind(P,A,B,C,L,S %*% rbind(A,B,C))
# 3Dplotの３軸が等長になるようにちょっと工夫
rg <- range(X)
X <- rbind(X,rep(rg[1],3),rep(rg[2],3))
# ３次元プロット
plot3d(X)
# P,A,B,Cを強調してプロット
spheres3d(P,color="red",radius=0.05)
spheres3d(rbind(A,B,C),color="blue",radius=0.05)

# Lが面をよぎる点は、L上の点のうち、任意の面上の点と最短距離の点(ここではAを使った)
tmp <- apply((t(L)-A)^2,2,sum)
selected <- which(tmp==min(tmp))
# Lが面をよぎる点
M <- L[selected,]
# 面に対してPと対称な点は、PからM方向にMの２倍の距離進んだところ
Q <- P + 2 * t[selected] * n/sqrt(sum(n^2))

spheres3d(M,color="green",radius=0.05)
spheres3d(Q,color="purple",radius=0.05)
Q

• • 問２　４タイプの等確率サンプリングで、n回目に初めて特定のタイプが観察され、1-(n-1)回目までに残りの３タイプが１回以上観察される確率
  • 乱択実験する

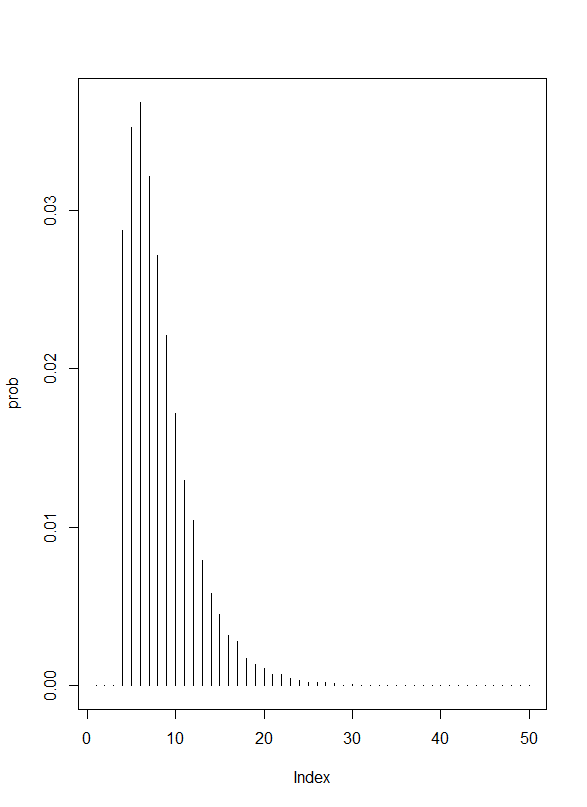
# 実験回数は十分に
n.trial <- 10^5
# １実験ごとにせいぜい50回も観察すれば、特定タイプが1度は観察されるだろう
n.events <- 50
# 常に4タイプは等確率で観察されるから、実験回数ｘ観察回数の乱数を行列に納める
X <- matrix(sample(1:4,n.trial*n.events,replace=TRUE),ncol=n.events)
# 特定観察を１、それ以外の観察を２，３，４とする
# 1 :: "red"
# n番目で初めて１が観察されて、他の条件を満たす回数を数え上げる
prob <- rep(0,n.events)
# 最低でも４回抜き出しは必要
for(i in 4:n.events){
	# n番目が1="red"である試行回
	tmp <- which(X[,i] == 1)
        # n番目が1である試行回について取り出して
	tmpX <- as.matrix(X[tmp,1:(i-1)],ncol=i-1)
        # n-1回までに、少なくとも１回以上、2が観察され、１回以上３が観察され、１回以上４が観察され、１は１回も観察されていないことを
        # 以下のような計算式で表す
        # apply(tmpX-2,1,prod) は各行に少なくとも2が１回以上あれば0となる。それが3でも4でもそうなることは、足し合わせても０のまま、と言える
        # さらに、apply(tmpX-1,1,prod)が0でないことは、1,,,(n-1)に1が観察されていないことを表す
	tmp2 <- (apply(tmpX-2,1,prod) + apply(tmpX-3,1,prod) + apply(tmpX-4,1,prod)) == 0 & (apply(tmpX-1,1,prod) !=0)
        # tmp2のうちTRUEの数を数え、総実験回数で割ってやれば、そのような確率が解る
	prob[i] <- sum(tmp2)/n.trial
}

plot(prob,type="h")

• □２　２次曲線 上の点接線とｘ軸の交点距離の最小値
  • 1.303222 くらい

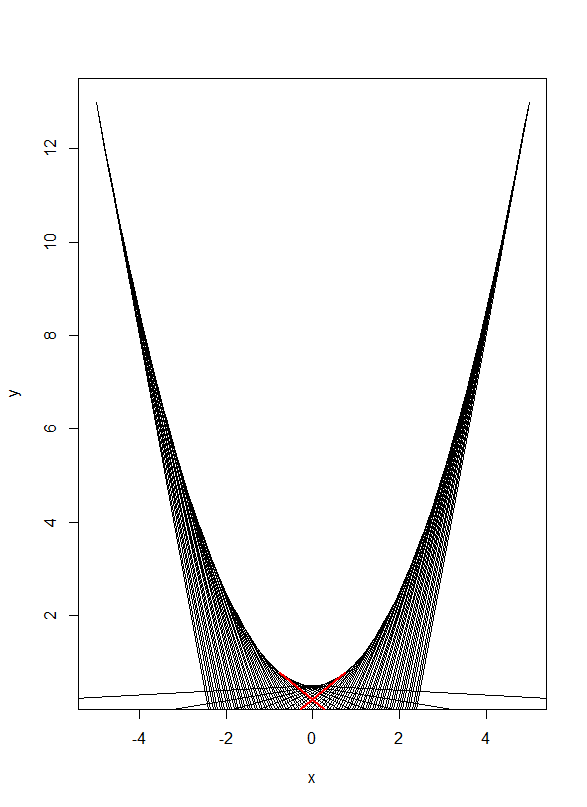
x <- seq(from=-5,to=5,length=100)
y <- 1/2 * (x^2+1)

plot(x,y,type="l")
L <- rep(0,length(x))
for(i in 1:length(x)){
	Qx <- x[i]-y[i]/x[i]
	Qy <- 0
	L[i] <- sqrt((x[i]-Qx)^2 + (y[i]-Qy)^2)
}

s <- which(L==min(L))

min(L)

plot(x,y,type="l")
for(i in 1:length(x)){
	Qx <- x[i]-y[i]/x[i]
	Qy <- 0
	segments(x[i],y[i],x[i]-y[i]/x[i],0)
}

for(i in 1:length(s)){
	Qx <- x[s[i]]-y[s[i]]/x[s[i]]
	Qy <- 0
	segments(x[s[i]],y[s[i]],x[s[i]]-y[s[i]]/x[s[i]],0,col="red",lwd = 2)
}

• □３　の和
  • 収束するなら計算機は得意
  • だいたい　1.476627 ()

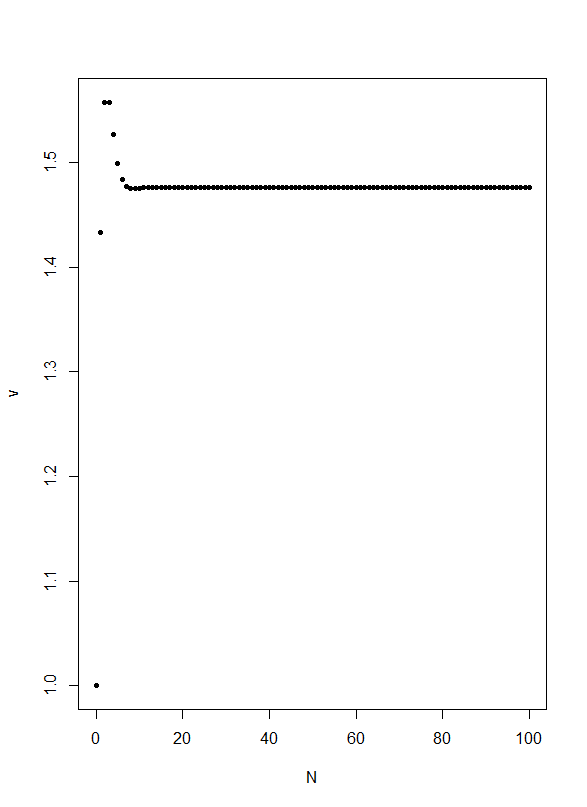
N <- 0:100

v <- rep(0,length(N))

for(i in 1:length(N)){
	v[i] <- sum((1/2)^(0:N[i]) * cos((0:N[i])*pi/6))
}
plot(N,v,pch=20)
v[length(v)]

• □４　の曲線の長さ
  • 細かく点列を作って、折れ線の長さを求めれば近似値は求まる
  • 1.762747くらい (2log(sqrt(2)+1))

x <- seq(from=0,to=pi/2,length=10000)

y <- log(1+cos(x))

plot(x,y,type="l")

diff.x <- diff(x)
diff.y <- diff(y)

L <- sum(sqrt(diff(x)^2+diff(y)^2))
L

• □５　の２点B,Cを底辺とした2等辺三角形の頂点がy軸上にあるとき、それは正三角形であるから、外心が原点で半径が２であるような三角形ABCについての問題である
  • 原点中心の円周上に３点を持つ三角形の垂心座標は、(3点のx座標の和,3点のy座標の和)となることを使えば、以下のように、黒がAの座標で半径２の円周、緑と青で描かれれる円が、垂心座標であり、そのうち、青がAのｙ座標が正の場合

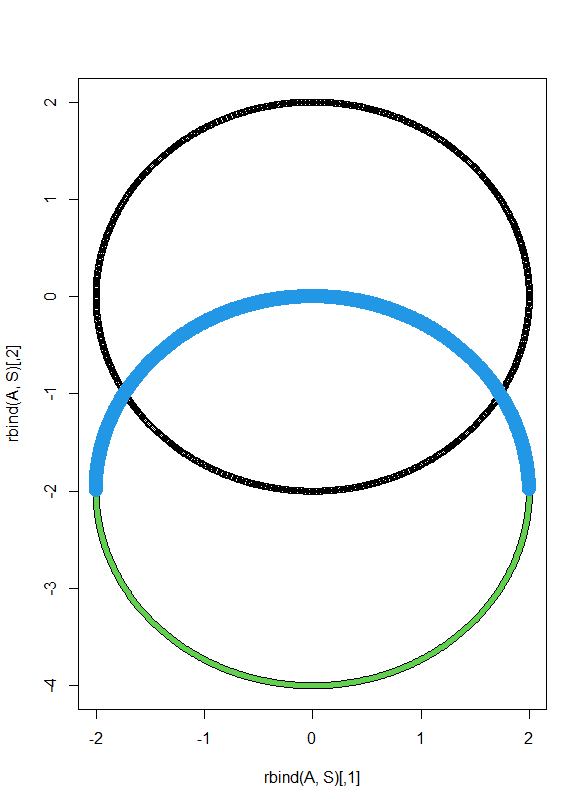
B <- c(-sqrt(3),-1)
C <- c(sqrt(3),-1)
t <- seq(from=0,to=1,length=1000) * 2 * pi
A <- cbind(2*cos(t),2*sin(t))


points(B[1],B[2],pch=20,col=2)
points(C[1],C[2],pch=20,col=2)

# 単位円周上に３点を持つ三角形のの垂心は(xa+xb+xc,ya+yb+yc)なので
# 半径２の円周上の場合も同じ

S <- cbind(A[,1]+B[1]+C[1], A[,2]+B[2]+C[2])
plot(rbind(A,S))

points(S,pch=20,col=3) # 垂心をプロット

posi <- which(A[,2]>0) # Aのy座標が正のものを取り出す

points(S[posi,],pch=20,cex=3,col=4)

• □６
  • 問１　素数。が素数なら 、nは素数
    • 対偶。nが素数で内ならは素数ではない
    • いずれにしても、無限に大きい数に関して、ルールがはっきりしない素数に関する「証明問題」は単なる例示的計算機利用は苦手

library(primes)

n <- 2:10000
K <- 3^n - 2^n

p.or.notp.1 <- is_prime(K)

p.or.notp.2 <- is_prime(n)

# 3^n - 2^nが素数ならnは素数
table(p.or.notp.2[which(p.or.notp.1)])
# その逆は真ではない
table(p.or.notp.1[which(p.or.notp.2)])

# 対偶
# nが素数でないなら、3^n-2^nは素数ではない
table(p.or.notp.2[which(!p.or.notp.2)])
# その逆は真ではない
table(p.or.notp.2[which(!p.or.notp.1)])

• • 問２　点(1,p)　と　点(a, ap) (a > 1)とを通る微分可能な関数の接線の中に原点を通るものがあることを示す
    • ２点を通り、一般性のある微分可能な関数を描いて見せて、原点を通る直線のなかに、接線になりそうなものがありそうなことを図示して、それっぽさを示すことにする
    • という関数はg(x)が微分可能な時、確かに、(1,p)を通り、(a,ap)を通る

# f(1) = pとする

p <- 1.3  
a <- pi/2 
# 適当な微分可能な関数
g <- function(x){
	sin(x^2) + 3 * x + 0.2 * x^2 - 0.004 * x^3 + 5
}

f <- function(x,p,a){
	0.1 * (x-1) * (x-a) * g(x) + x * p
}

x <- seq(from=-3,to=3,length=100)

y <- f(x,p,a)

plot(x,y,type="l")
# (1,p), (a, pa)を通ることを図示
abline(v=1)
abline(v=a)
abline(h=p)
abline(h=p*a)

# 原点を通る直線を放射状に描く
t <- seq(from=0,to=1,length=25) * 2 * pi

for(i in 1:length(t)){
	abline(0,tan(t[i]),col=2)
}

小行列式 minor と Flag minor

• nxn正方行列から、m x m ()正方行列はたくさん作れる
• 抜き出す行と列とを同じにすれば、個　(0x0行列、nxn行列も含めて)作れるが
• 抜き出す行と列とを違えれば、もっと多くなる
• そんなすべての本当にすべての正方行列の行列式がすべて正になるような行列をTotal positiveと言う(非負になるときは、Total non-negative)
• ちょっと数が多すぎるが、その数を制約するやりかたに、Flag minorと言う取り出し方がある
• これは、n行から、m行を取り出す。この取り出し方は、通り
• 列の取り出し方は、左詰めで、第１列から第m列にする
• このような取り出し方で取り出される部分正方行列の行列式をFlag minorと呼ぶ
• このFlag minorには、次のような関係がある
• 行列の行の順を考慮して、なる関係にあるような、順序番号 があるとする
• それ以外の順番は増えてもよいものとして、それらを、とすると
• , のペアと、,のペアと、,のペアとを考えた時
• という関係がある
  • ただし、はいずれも、Flag minor
• この関係があるので、Flag minorの値の間には相互関係がある
• この相互関係をたどると、すべてのFlag minorが正であることを確認するためには、限定されたFlag minorが正であることを確認すれば事足りることが解る
• 実際、Flag minorの数はあるが、符号を確かめるべきFlag minorの数はであることが知られている
• さらに、個のある取り方をしたFlag minorを固定すると、残りの確認すべきFlag minorの数はと知られており、この個のFlag minorsの団同士に団代数的構造が入っていることが知られている
• こちらを参照
• 具体的には、確かめればよい、Flag minorのセットには次のようなものがある
  • と。これが固定分で、全部で2(n-1)個
  • 入れ替え可能だが、とりあえず固定する例として、,,,....
  • この個数は、
• Flag minorのPtolemy 的関係の実験が以下のRコード

n <- 8
M <- matrix(rnorm(n^2),n,n)

a <- 5
b <- c(3,6)

commons <- c(2,4,7)

t1 <- sort(c(commons,b))
t2 <- sort(c(commons,a))

u1 <- sort(c(commons,b[1]))
u2 <- sort(c(commons,b[1],a))

v1 <- sort(c(commons,b[2]))
v2 <- sort(c(commons,b[2],a))

det(M[t1,1:length(t1)]) * det(M[t2,1:length(t2)])

det(M[u1,1:length(u1)]) * det(M[v2,1:length(v2)]) + det(M[u2,1:length(u2)]) * det(M[v1,1:length(v1)])

Plucker座標

• ３次元空間の直線を考える
• 直線上の２点のユークリッド座標を決めれば、その直線上の点の座標を計算することができる
• 別の方法で直線に座標を与えたい
• ２点のユークリッド座標の代わりに、その斉次座標を考える
• この２点は、と４つの値の組で表現できる
• 射影幾何的には、が等しい点の集合が原点を通る４次元空間の直線ともみなせる
• 今、３次元空間の２点を通る直線を考えると、第１点の自由度は３、方向ベクトルを定めると、自由度は２なので、併せて自由度は５
• 斉次座標的に自由度５のものを定めるには、６つの値の組であればよいことになる
• その作り方が以下のようになる
• なる２ｘ２行列を６個、作る
• それぞれの２ｘ２座標の行列式 の値を取ると、６個の値が作れる
• 並べ方は。ただし、は、の行列式になっている
• この６個の値の組をPlucker 座標と言う
• また、この６個の値の組の代わりになる２ｘ２行列を１６個、作り、４ｘ４行列の成分とする
• その４ｘ４行列の成分とすると、対角成分は０で、反対称行列になる。したがって、情報は冗長で、あくまでも６つの値で決まる行列であるが、反対称行列が出てくるところが、団代数的。
• ちなみに、この直線をある２点の斉次座標から定めたが、別の２点のペアから始めても、得られる６つの値の組は「同じようなもの」にならなければ、この方法がうまく行っていることにはならない
• 別の２点の斉次座標は、最初の２点の斉次座標の線形和で表される(射影幾何のルール)。しかも線形独立
• そのような別の２点の斉次座標から、２ｘ２行列を取り出してその行列式を計算すると、元の対応する行列式にある値をかけたものになっており、その「ある値」は、２ｘ２行列の取り出し方によらず同じである(ちなみにその「ある値」は、はじめの２点の斉次座標を並べた４ｘ２行列Ｍと、別の２点の４ｘ２行列Ｍ’との間に、と言う関係がある(ただしは２ｘ２行列)ときの、の行列式になっている。これは、正方行列が積の関係のとき、であることからわかる
  • このと表せることが、「別の２点の斉次座標は、元の２点の斉次座標の線形和」ということ
• この意味で、６つの値のペアは、どんな２点をとっても、その比は同じと言う意味で斉次座標的な性質になっている
• ちなみに、Plucker 座標系は、グラスマン座標系の特別な場合(Mathwordlの記事参照)
  • グラスマン多様体は、n次元空間に張られる、0,1,2,...,n次元線形部分空間を全部ひっくるめたもの
  • 特定のk次元部分空間をまとめたものをG(k,n)と書く
  • このとき、個の、det(kxk行列)がグラスマン多様体
  • Plucker座標は、k= 2のときで、３次元空間の場合は、n=3だから、だから、６変数座標

# plucker座標算出関数
my.plucker <- function(x0,y0){
  X0 <- c(1,x0)
  Y0 <- c(1,y0)
  
  M0 <- cbind(X0,Y0)
  
  p.id <- rbind(c(1,2),c(1,3),c(1,4),c(3,4),c(4,2),c(2,3))
  p0 <- rep(0,6)
  for(i in 1:6){
    tmp <- M0[p.id[i,],]
    p0[i] <- det(tmp)
  }
  p0
}

my.plucker.matrix <- function(M0){
 
  p.id <- rbind(c(1,2),c(1,3),c(1,4),c(3,4),c(4,2),c(2,3))
  p0 <- rep(0,6)
  for(i in 1:6){
    tmp <- M0[p.id[i,],]
    p0[i] <- det(tmp)
  }
  p0
}
# 直線を通る２点
x0 <- rnorm(3)
y0 <- rnorm(3)
p0 <- my.plucker(x0,y0)
p0
# この直線を通る別の２点

t <- rnorm(2)

x1 <- x0 + t[1] * (y0-x0)
y1 <- x0 + t[2] * (y0-x0)

p1 <- my.plucker(x1,y1)
p1

p1/p0

## 線形変換

M0 <- cbind(c(1,x0),c(1,y0))

n.pt <- 100
ps <- matrix(0,n.pt,6)
Lambdas <- list()
for(i in 1:n.pt){
  tmp <- matrix(rnorm(4),2,2)
  Lambdas[[i]] <- tmp
  Mtmp <- M0 %*% tmp
  ps[i,] <- my.plucker.matrix(Mtmp)
}

ratio.rows <- apply(log(abs(ps)),2,diff)
range(apply(ratio.rows,1,diff))

トロピカル代数のためのメモ

• こちらの団代数の短い文書を読むときのメモ
• 半体
  • 集合があって、２つの演算が定まっている
  • ２つの演算は、積と和
  • ただし、和については「加えることはできるがその逆である引くことはできない」
  • ３つの半体を覚える
    • 自明半体
      • 要素は１だけ。１と１の積が１、１と１の和も１
    • 普遍半体
      • n個の変数の多項式を要素とする
      • ただし、多項式には条件がある
      • 特定の整数係数多項式をまず定める
        • 係数は非負。その多項式は0であってはいけない
      • このような０でない、非負整数係数多項式の有理式として表される関数全体が集合
      • 和と積とは通常の和と積と定めると、この関数全体が半体になっている。これが普遍半体
    • トロピカル半体
      • n個の変数
      • そのローラン単項式全体 を考える
        • これは普遍半体での「0でない、非負整数係数多項式」の有理式として表される関数全体の集合に対応する
      • 積は普通の積とする。これにより、変数ごとの次数は「普通の和(加算と減算)」に相当する
      • 和は、変数ごとの「次数の最小値」とする
      • これが半体となっており、積が(次数の)和になり、和が(次数の)最小を取る操作になっていることから、その性質がトロピカルだということでトロピカル半体と呼ばれる
  • 普遍半体のトロピカル写像
    • 普遍半体とトロピカル半体とには対応関係(準同型写像)があるので、普遍半体の要素である非負整数係数有理多項式に対応するトロピカル半体のローラン単項式が得られる
      • 例
        • -> トロピカル半体には、「整数係数」という概念がないから、それは単純に消失する
        • 
• 半体を用いた群環
  • 半体は、群であって、不完全な体の性質を持っているので、群ではある。これをPと表すとする
  • 群環は、群の要素に係数を掛けたものの線形結合。係数には体が使われる
  • ただし、この群環に用いられる線形結合の加算は、トロピカル加算ではなくて、普通の加算
  • いずれにしろ、半体を群として整数を係数とした群環が定義できる。これをZPとする
  • さらに、そのような群環ZPの分数体も作れて、それをQPとする。これは体になっている
• 団代数
  • 団代数では、変数の個数nを定め
  • 半体Pを定める
  • そのうえで、そのQPも現れて、説明される
  • ランク n は変数の個数
  • (B,x,y)をPに係数を持つ種子と言う
    • nxn 反対称行列B
    • 。ただし、はQPを係数とする有理関数体で、代数的に独立。団変数
    • 。係数
  • 種子には、n通りの変異が定まり、n変異種子は、種子としての性質を持つので、種子の集合はn正則グラフになっている
  • ある種子を１個取ると、n正則木の全ノードに対応する種子が一意に定まる
  • したがって、各種子のx (QPを係数とする有理関数体を要素とする、要素数nの集合)の集合がとれる
  • xの要素は１変異につき、１要素が変化するが、こうして、xの要素として現れるQPを係数とする有理関数体の要素全体の部分集合は、FのZP部分代数になっている。これが初期種子によって定まる団代数であるとして、団代数が定義される。。。ZP部分代数のZがちょっとわかっていないが、n個のうちの第i番目の方向について１歩進む、２歩進む、１歩戻る、という動きがZ(整数)的、ということらしい
  • xの変異は、i番目での変異のとき、i番以外の要素は変化せず、i番目が次のように変化する
    • 
  • すごく小難しいが、Fの要素であるxに関する有理式であることがまずわかる
  • また、xに関する部分以外が係数になるが、その係数は、半体Pの要素であるyに関する群環ZPの分数体であるQPになっていることもわかる
  • したがって、xの変異に伴う変換は、QPを係数とする有理変換である、と読める
  • つまり、初期種子のxから一意に決まるxの要素たちは、xのQP係数有理関数であることは、その式変形からわかっている
  • 団代数として面白いのは、式変形からわかっている、この事実以上に制約が厳しい事実が潜んでいることである
• 団代数の特徴
  • x変数はxのZP係数のLaurent多項式になる、というのが、その厳しい制約である
• この文書が強調したこと
  • n正則グラフの頂点集合が、何かしらの対象空間を表しているとき、その個々の頂点～種子とy変数の構成要素の組が、何かしら、その種子特有の状態を表しているので、y変数を知ることや、異なる種子のy変数を比較することに意味があるのは当然として、そこに、トロピカル化写像を行ってy変数をトロピカル化したときにそこに得られる情報と１対１対応していることを強調している。トロピカル化写像によりy変数は、その「主要部取り出し」をしているとみなせるが、「主要部取り出しをしてしまっても」情報が残っている、ということになるらしい
• 何かうまいことを考えて、対象を変異で移り変わるn正則グラフに載せることができたなら、この強調点を応用できることになる

sagemath をcygwinで

• sagemathは数学のアプリケーション
• こちらからWindows用にダウンロードしてさくっと使えるのですが、追加のpython packageを入れようとすると：
  • sageshell を立ち上げて"pip --install hogePackage" とすればよいはずなのだが、openSSLがうまく行かずに失敗する
  • "pip --install hogePackage"はPyPIからダウンロードするコマンドなので、そこにopenSSLでアクセスできないだけなら、zipファイルをローカルに取得して、"sage --pip install ~/Downloads/packagename.zip”のようにすれば良いはずだが、今度は、コンパイラ問題でうまく行かない
• sagemathをcygwin環境に入れるとうまく行くかも、ということで、こちらに沿ってやってみる
  • まず、cygwinをこちらに沿って取ってきてローカルにインストールする
  • 何も考えずにcygwinをインストールし、cygwinを立ち上げれば、仮想環境
  • そこで、sagemathのcygwin環境セットアップのページ(こちら)に戻って、言われた通りに以下のコマンドを、cygwinのコマンドラインに入力する

curl -OL https://rawgit.com/transcode-open/apt-cyg/master/apt-cyg
install apt-cyg /usr/local/bin
rm -f apt-cyg

apt-cyg install make m4 flex git gcc-core gcc-g++ gcc-fortran diffutils \
                  liblapack0 liblapack-devel zlib-devel libreadline-devel \
                  libiconv-devel libcrypt-devel openssl-devel gettext-devel \
                  python ccache

• • すると、wgetがないよ、とのエラーが出るので、こちらを参考に、cygwinのインストール exeファイルを再度実行して、途中に現れる、追加オプションでwgetを指定して、cygwin環境にwgetを追加する
  • そのうえでcygwinを立ち上げ、再度

apt-cyg install make m4 flex git gcc-core gcc-g++ gcc-fortran diffutils \
                  liblapack0 liblapack-devel zlib-devel libreadline-devel \
                  libiconv-devel libcrypt-devel openssl-devel gettext-devel \
                  python ccache

• • とやるとうまく行くので、cygwinインストール解説のoptionalは飛ばして

git clone --branch develop git://trac.sagemath.org/sage.git
cd sage

• • (sagemathのページにはないが)

cd sage

• • として、Makefileのあるディレクトリに移動し

make

• • とする
  • すると、configureしてからじゃなきゃだめ、とのメッセージが出るので、そりゃそうだ、と思い直して

./configure

• • とし(こちら参照)、長い、ログ表示を待ち、再度

make

• これでcygwin環境にて、sagamathのソースを入手し、コンパイルしてのインストールが終了...
• なのだが、makeにものすごい時間がかかり、終わってみれば、エラーあり。。。
• ただし、Cygwinのsageディレクトリ配下に 実行可能な sage コマンドが現れinteractive sageが立ち上がりはした。とはいえ、新たに pip install hogepackageは相変わらずうまく動かなかったので、目的は達成できなかったという残念な結果