遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

pythonでigraphを使ってplotする

python igraph pycairo
  • igraphはRとpythonで使えるグラフ理論パッケージ
  • python(python3)をanaconcaでwindowsに入れて pip install python-igraph したものの、プロット機能が使えなくて難航
  • pycairoに依存しているということがわかり、そのためにcairoを入れる必要があったのでメモ
  • こちら
  • msysを入れて…とひと手間かけたが、結局、コマンドラインから
conda install pycairo
  • とするだけでよいらしい
  • 入れた結果
import igraph
g = igraph.Graph()
g.add_vertices(3)
g.add_edges([(0,1),(1,2)])
adj = g.get_adjacency()
g2 = igraph.Graph.Adjacency(adj.data) # adjはigraphパッケージ独特な Matrxiと言うクラスなので、そのデータ部分だけを取り出して、リストとした adj.dataをGraph.Adjacency()関数に渡す
igraph.plot(g2)
out = igraph.plot(g2)
out.show()
out.save(fname='out.pdf')

f:id:ryamada:20201206094624j:plain

ガウシアンカーネルの無限次元性

サポートベクターマシン カーネル関数 カーネルトリック ガウシアンカーネル
  • サポートベクターマシンではカーネル関数を使って、高次元空間に投げ上げて、そこでの内積を利用する
  • 観測変数を組み合わせて新たな次元軸を作って、その増やした次元での内積を計算するときに、地道に計算してもよいけれど、うまい方法があるといいな、と。
  • そのうまい方法を用いるのが「カーネル・トリック」を使う、という話
  • この記事は解りやすい
  • 手作業で新たな変数を作り出し、それに対する「トリック」を紹介してくれて、最終的に、ガウシアンカーネルを紹介し、それが「無限の変数」を作り出してその内積を計算してくれていることを紹介している
  • 残念なのは、そのガウシアンカーネルが分解されて、無限次元に飛んでいるところの説明式の符号が間違っていること…。正しい式はこちらにあるように、以下の式
    • K(x_1,x_2) = exp(-\frac{||x_1-x_2||^2}{2\sigma^2}) = exp(-\frac{||x_1||^2}{2\sigma^2}) exp(-\frac{||x_2||^2}{2\sigma^2}) exp(\frac{\text{innerProd}(x_1,x_2)}{\sigma^2})
  • これを展開すると
    • K(x_1,x_2) = exp(-\frac{||x_1||^2}{2\sigma^2}) exp(-\frac{||x_2||^2}{2\sigma^2}) \sum_{i=0}^{\infty} \frac{\text{innerProd}(x_1,x_2)^i}{i!}
  • 指数関数を使わず、ある程度の項数で近似するなら、内積だけ計算しておけばよいこともわかる
  • 念のため、この展開の収束をRでやっておくと：
d <- 5

x1 <- rnorm(d)
x2 <- rnorm(d)

V <- exp(-sum((x1-x2)^2)/2)

C <- exp(-sum(x1^2)/2) * exp(-sum(x2^2)/2) 

n <- 0:10

v <- rep(0,length(n))

v[1] <- C

for(i in 2:length(n)){
	#v[i] <- v[i-1] +C* sign(-1)^n[i] * sum(x1*x2)^n[i]/factorial(n[i])
	v[i] <- v[i-1] +C * sum(x1*x2)^n[i]/factorial(n[i])
}

plot(n,v)
abline(h=V)

三角化・結び目・団代数・双曲幾何・確率論・量子確率論～たまった資料の整理をする

はじめに

  • コロナ禍のため(？)に資料を読み捨てにして整理せずにいたら、収拾がつかなくなってきたので、いったん整理する

団代数

三角化

結び目・結び目補空間・3-多様体

双曲幾何

代数と幾何

Teichmuller space

曲面解析・変形

  • Hyperbolid Harmonic Mapping for Surface Registration : 曲面のハンドリング。{Ricci flow、双曲幾何構造分解としてのパンツ分解、等温座標系、共形変換} = {Discrete Hyperbolic Ricci Flow, Hyperbolic Pants Decomposition, Homotopy Class, Non-linear Heat Diffustion}
  • Recent Advances in Computational Conformal Geometry(2009) : 曲面の共形変換の総説。Ricci flowベースで説明しつつ、Teichmuller spaceと言う単語への言及もある。Ricci flowで変形して、hyperbolic uniformization metricを計算することができる、その後、パンツ分解をすることで、Fenchel-Nielsen coordinatesを付与することによりTeichmuller spaceとつなげることができる　

トロピカル代数・トロピカル幾何

Circle packing, Sphere packing, Applonian circles

行列に関すること

量子確率論

sagemath snappy のドッカーを使ってみる

Docker sagemath snappy
  • こちらにトポロジーツール"snappy"をsagemathと連携して使う環境づくりについて説明してある
  • 結局、dockerで諸々を入れるのが良いということらしいのでdockerhubにあるcomputop/sageをドッカーで入れることにする
  • そのためにまず(Windows環境で)dockerが使えるようにすることにする
  • こちらからドッカー環境をローカルPCに作る
  • Get dockerして、ダウンロードされたexeファイルを実行するだけ
  • デスクトップにできたドッカーイメージをダブルクリックして開始。
  • すると、Linux カーネル更新プログラム パッケージを入れろ、と言われるので、こちらのx64 マシン用の最新の WSL2 Linux カーネル更新プログラム パッケージをダウンロードしてください。をクリックして、言われるがままに実行する。
  • そのうえで、Dockerを再起動すると、Docker環境らしきものが立ち上がり、右側にコマンドを打てる場所が現れる
  • 今、使いたいsagemathとsnappyが連携している「もの」を入れるべく、このサイトのコマンドを、Docker内のコマンドプロンプトに打っていく
  • そもそも、最初のコマンド(以下)にかかる時間が長い…sagemath本体を入れているからだろう…
docker pull computop/sage
  • 引き続いて
docker run -it computop/sage
  • とやると、どうやら、ドッカーイメージが「入った」ことになるらしい
  • Dockerのアイコンをダブルクリックするとドッカーが立ち上がったよというメッセージが出るので、そうしたら、コマンドプロンプトで
docker run -it -p 127.0.0.1:8888:8888 computop/sage
||
-と打つ。その上で
>||
$ sage --notebook

とすると

Starting up Sage Jupyter Notebook, viewable at http://localhost:8888
  • と出るので、ブラウザにてhttp://localhost:8888を開くと、いわゆるJupyter notebookの画面となるから、そこでsagemathのノートを開く

f:id:ryamada:20201024085551p:plain

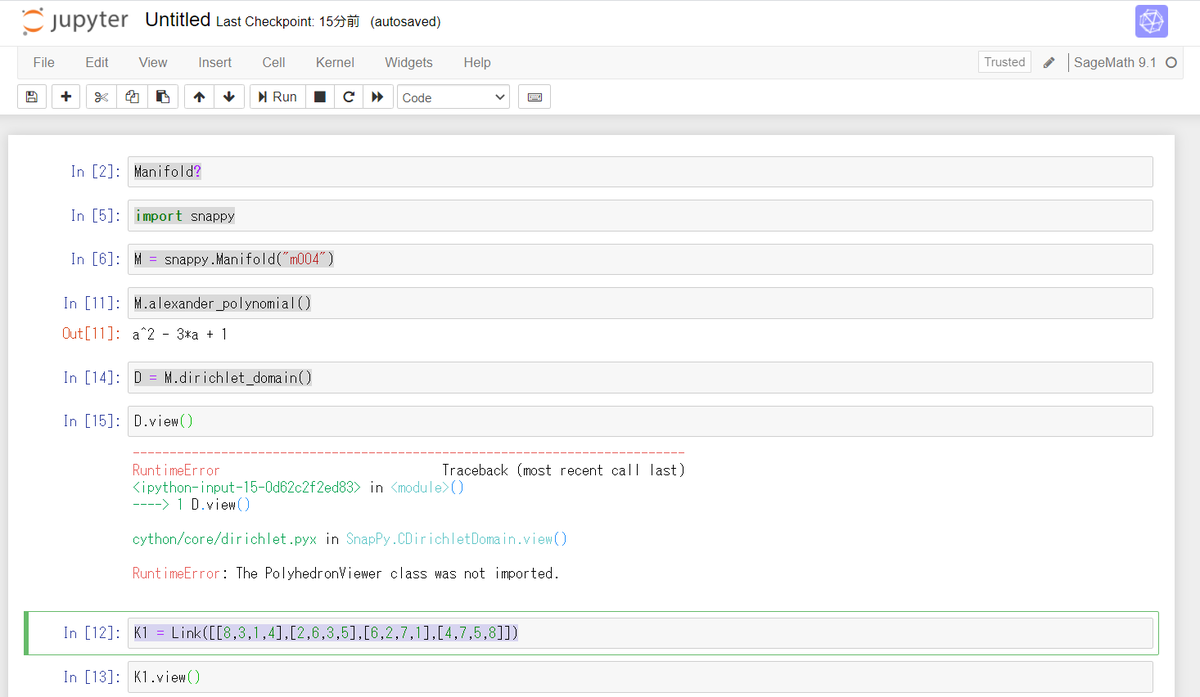
Manifold?
import snappy
M = snappy.Manifold("m004")
M.alexander_polynomial()
D = M.dirichlet_domain()
K1 = Link([[8,3,1,4],[2,6,3,5],[6,2,7,1],[4,7,5,8]])
  • とか、する。
  • お絵描きがまだうまく動かないのだが…

f:id:ryamada:20201024085611p:plain

双曲幾何とポアンカレ半平面と射影変換

双曲幾何 ポアンカレ半平面
  • 双曲幾何空間をポアンカレ半(超)平面で表すモデルの話と、それが射影変換で自由に等距離的に変換される話
  • Wiki記事の話をRでなぞって確かめる