2017-02-04

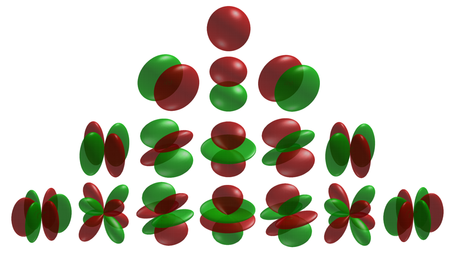
球面調和関数

球面調和関数ルジャンドル多項式ルジャンドル陪多項式

この絵(球面調和関数)を定性的に説明したい
中央に並んだ絵は、球面上の色模様にしろ、くびれ的描図にしろ、z軸に関して回転対象
黄色を正、緑を負とすれば、「正」「正負」「正負正」「正負正負」「正負正負正」となっている
これは、z軸座標([-1,1])について、『ルジャンドル多項式』に比例した値が張り付いているから

このルジャンドル多項式は[-1,1]の範囲の連続関数で、すべて(1,1)を終点としている。始点は偶数(0,2,...)番目では(-1,1)に、奇数(1,3,...)番目では(-1,-1)になっている
第i番目のルジャンドル多項式は、y=0との交点をi個持つ
x=0に関して線対称であるか、(0,0)に関して点対称
球面調和関数の中央のそれはl=0,1,2,...,に対してm=0のものだが、そのような球面調和関数は、z軸の座標(角座標を使えば $\cos{\theta}$ で表されたルジャンドル多項式の値に相当するものとなっている
このことは、ルジャンドル多項式 $P_l(x)$ はルジャンドル陪多項式 $P_l^m(x)$ の $m=0$ のそれであって、球面調和関数が $Y_l^m \propto P_l^{|m|}(\cos{\theta})e^{im\phi}$ と表され、中央の列の球面調和関数は $m=0$ の場合であることからも対応がとれる
このように球面調和関数のセットではz軸が特別扱いされている
球面調和関数の中央ではないそれについて着目しよう
$m \ne 0$ である球面調和関数はルジャンドル陪関数のうち、 $m=0$ に対応するルジャンドル多項式でないものに対応するから、ルジャンドル陪関数がどうなっているかを確認する必要がある

この図はルジャンドル陪関数の図だから、ルジャンドル関数(m=0)とそれ以外とが両方とも描かれている。ルジャンドル関数(m=0)は実線、m=0でない陪関数は破線である
破線(m=0でない陪関数)の特徴は、[-1,0]に始まり[1,0]に終わっていることである
m=0であるルジャンドル関数はすべて[1,1]で終わり、[-1,1]もしくは[-1,-1]を始点とするのと対照的である
この[-1,0]に始まり[1,0]に終わるということに注目して、非中央列の球面調和関数を見ると、z=-1,1では白い色(値が0)になっていることがわかる。これは、 $Y_l^m \propto P_l^{|m|}(\cos{\theta})e^{im\phi}$ からもわかるとおり、z座標 $\cos{\theta}$ の値が-1,1のときにm=0でないルジャンドル陪関数の値が0になることと対応づく
ルジャンドル陪関数は、同じlのルジャンドル関数(m=0の場合)の始点が[-1,-1]のときには、[-1,0]から減じる方向にスタートし、ルジャンドル関数がの始点が[-1,1]のときには[-1,0]から増加する方向にスタートする
また、ルジャンドル陪関数のm=0の場合(ルジャンドル関数の場合)のy=0との交点の数は、l個であるが、ルジャンドル陪関数のそれは(両端[-1,0],[1,0])を除くとl-|m|個となる
mが0でない場合のy=0との交点の数は、球面調和関数で値が0(球面表示なら白い緯線、くびれ表示なら、z軸方向でのくびれ)に相当する
また $Y_l^m \propto P_l^{|m|}(\cos{\theta})e^{im\phi}$ という球面調和関数表現からもわかるように、 $\phi$ という経度について、m=0ならは１周にくびれはないが、|m|=1なら $0->2\pi$ 分の三角関数の上下があるから、白い経線が(相互に180度の間隔で)2本入る。|m|=2なら2周期分となり90度ずつ4本、|m|=3なら3周期分の60度ずつ6本、となる
結局、l,mが与えられると、白い緯線がl-|m|本、白い経線が $2\times |m|$ 本入るから、白い領域で区画された領域は $m\ne 0$ のときは $(l-|m|+1) \times 2|m|$ 個、 $m=0$ のときは $(l+1)$ 個できる
mが正のときと負のときの関係

中央の列はm=0なので対象外
中央から左右1列目、3列目では、赤・緑が反転している
中央から左右2列目(、描かれていないが、偶数列目)では、赤・緑が反転せず、どまったく同じ絵柄
これは、 $Y_l^m \propto (-1)^{\frac{m+|m|}{2}}P_l^{|m|}(\cos{\theta})e^{im\phi}$ の式の $(-1)^{\frac{m+|m|}{2}}$ は、mが負であるなら、常に1、mが正であると、偶数のときは1、奇数のときは(-1)であることと、 $e^{im\phi}=\cos{m\phi} + i \sin{m\phi}$ の部分はmの正負によらず $\cos{m\phi}$ という実部だけを問題に(今はする)し、 $\cos{\alpha}=\cos{(-\alpha)}$ という関係があるからである