遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

球面三角形

球 球面 オイラー三角化
  • 単位球面S2を考える
  • S2上の任意の２点x,yについて、その２点を通る大円を定める
  • 今、x,yの順序を考慮するとき、この大円は方向を持つ
  • 方向を持つ大円は球面を進行方向右側半球面と進行方向左側半球面とに分ける
  • 球面上の第３点zはこの大円上の点であるか、左右半球面上の点であるかの３つの場合に分かれる
  • 今、球面上に３点x,y,zがあるとき、その順序 x,y,zを定めると、x,yが定める大円、y,zが定める大円、z,xが定める大円が囲む球面三角形の内部か、外側であるところの外部か、三角形上であるかの３通りに分かれる。その判定は、大円による左右半球判定のAND x AND判定かそれ以外かに分かれる
  • これを組み合わせることで球面上の３点からスタートし、それが作る球面三角形２つのうちの１つの内部の点を二つv1,v2を作り、球面三角形の２頂点u1,u2を定めることで、二つの球面三角形v1,u1,u2、v2,u1,u2を作ることができ、どちらの三角形が今考えているところの球面三角形の「内部」という意味合いで大きいかが定まる
  • 小さい方の三角形は三点を通る円周とし、大きい方も三角形にせず、その三点を結ぶ大円ではない円とすることで、オイラー三角分割ルールを守りながら、どんどん、分割を細かくすることができる
  • ...はずである
  • まずは下準備
    • 球面上の２頂点を与えて、その大円弧を決める
    • 球面上の３頂点を与えて、それを通る円弧を決める
library(onion)
library(rgl)

my.rsphere <- function(n){
	ret <- matrix(rnorm(n*3),ncol=3)
	ret/sqrt(apply(ret^2,1,sum))
}

my.3d2quart <- function(x){
	if(is.vector(x)){
		x <- matrix(x,nrow=1)
	}
	x[,1] * Hi + x[,2] * Hj + x[,3] * Hk
}
my.quart23d <- function(h){
	t(as.matrix(Im(h))[2:4,])
}
my.greatcircle <- function(h1,h2){
	h3 <- h1 * h2
	theta <- acos(-Re(h3))
	list(v=Im(h3),theta=theta,start=h1,end=h2)
}

my.circle.3pt.check <- function(h1,h2,h3){
	# 三角形の２辺。向きも考慮
	h12 <- h2-h1
	h23 <- h3-h2
	# ３頂点ベクトルと回転軸ベクトルのなす角が等しいことを利用して、
	# ２辺ベクトルと回転軸ベクトルの内積が0であることを条件に回転軸ベクトルを算出
	# 回転軸ベクトルの和は、仮に１とする
	M <- matrix(c(i(h12),j(h12),k(h12),i(h23),j(h23),k(h23),1,1,1),byrow=TRUE,3,3)
	if(det(M)!=0){
		a <- c(0,0,1)
		# 回転軸ベクトルを単位ベクトル化し
		tmp <- solve(M,a)
		tmp <- tmp/sqrt(sum(tmp^2))
		v <- (Hi*tmp[1] + Hj*tmp[2] + Hk*tmp[3])
		# 向きを考慮した２辺のベクトル積と回転軸ベクトルの内積が負であるなら
		# 回転軸ベクトルの向きを反転させる
		if(-Re(v * (h12*h23)) < 0){
			 v <- Conj(v)
		}
		
		# 回転角を出すために以下をする
		# ３頂点と回転中心との結ぶベクトルの単位ベクトル(回転平面ベクトル)を作る
		h1.tan <- h1 + Re(v*h1)*v
		h2.tan <- h2 + Re(v*h2)*v
		h3.tan <- h3 + Re(v*h3)*v
		h1.tan <- h1.tan/Mod(Im(h1.tan))
		h2.tan <- h2.tan/Mod(Im(h2.tan))
		h3.tan <- h3.tan/Mod(Im(h3.tan))
		
		# 回転平面ベクトルのベクトル積と内積を使う
		h1h3 <- h1.tan*h3.tan
		h1h2 <- h1.tan*h2.tan
		
		# 回転平面上での頂点v1-v3、v1-v2の角を求める
		theta <- acos(-Re(h1h3))
		theta2 <- acos(-Re(h1h2))


		#re.h1h3 <- Re(h1h3)
		re.h1h2 <- Re(h1h2)
		# 回転平面ベクトルのベクトル積と回転軸ベクトルの内積(方向が同じ傾向か否か)の判定
		tq.h1h3 <- -Re(h1h3*v)
		tq.h1h2 <- -Re(h1h2*v)
		
		# 反時計回りの角に直すための修正
		if(tq.h1h3 < 0){
			theta <- 2*pi-theta
		}
		if(tq.h1h2 < 0){
			theta2 <- 2*pi-theta2
		}
		print(theta-theta2)
		#if(theta < theta2){
		#	v <- Conj(v)
		#	theta <- 2*pi - theta
		#	theta2 <- 2*pi - theta2
		#}
		p <- list(v=v,theta=theta,start=h1,end=h3)
	}else{
		# ３点が大円上に乗っているなら、大円情報を返す
		p <- my.greatcircle(h1,h3)
	}
	p
}
my.circle.3pt <- function(h1,h2,h3){
	# 三角形の２辺。向きも考慮
	h12 <- h2-h1
	h23 <- h3-h2
	# ３頂点ベクトルと回転軸ベクトルのなす角が等しいことを利用して、
	# ２辺ベクトルと回転軸ベクトルの内積が0であることを条件に回転軸ベクトルを算出
	# 回転軸ベクトルの和は、仮に１とする
	M <- matrix(c(i(h12),j(h12),k(h12),i(h23),j(h23),k(h23),1,1,1),byrow=TRUE,3,3)
	if(det(M)!=0){
		a <- c(0,0,1)
		# 回転軸ベクトルを単位ベクトル化し
		tmp <- solve(M,a)
		tmp <- tmp/sqrt(sum(tmp^2))
		v <- (Hi*tmp[1] + Hj*tmp[2] + Hk*tmp[3])
		# 向きを考慮した２辺のベクトル積と回転軸ベクトルの内積が負であるなら
		# 回転軸ベクトルの向きを反転させる
		if(-Re(v * (h12*h23)) < 0){
			 v <- Conj(v)
		}
		
		# 回転角を出すために以下をする
		# ３頂点と回転中心との結ぶベクトルの単位ベクトル(回転平面ベクトル)を作る
		h1.tan <- h1 + Re(v*h1)*v
		h3.tan <- h3 + Re(v*h3)*v
		h1.tan <- h1.tan/Mod(Im(h1.tan))
		h3.tan <- h3.tan/Mod(Im(h3.tan))
		
		# 回転平面ベクトルのベクトル積と内積を使う
		h1h3 <- h1.tan*h3.tan
		
		# 回転平面上での頂点v1-v3、v1-v2の角を求める
		theta <- acos(-Re(h1h3))

		# 回転平面ベクトルのベクトル積と回転軸ベクトルの内積(方向が同じ傾向か否か)の判定
		tq.h1h3 <- -Re(h1h3*v)
		
		# 反時計回りの角に直すための修正
		if(tq.h1h3 < 0){
			theta <- 2*pi-theta
		}
		p <- list(v=v,theta=theta,start=h1,end=h3)
	}else{
		# ３点が大円上に乗っているなら、大円情報を返す
		p <- my.greatcircle(h1,h3)
	}
	p
}

my.circle.on.sph <- function(p,n=100,mint=0,maxt=1){
	t <- seq(from=mint,to=maxt,length=n)
	theta. <- p$theta*t
	q <- cos(theta./2) + sin(theta./2) * (p$v)
	q * p$start * Conj(q)
}


R <- my.rsphere(5000)

h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))
h3 <- my.3d2quart(my.rsphere(1))
#h1 <- Hi*1
#h2 <- Hj*1
#h3 <- Hk*1
p <- my.circle.3pt(h1,h2,h3)
p.gc <- my.circle.on.sph(p)
p.gc2 <- my.circle.on.sph(p,maxt=1000)
plot3d(R)

points3d(my.quart23d(p.gc),col=2,size=5)
points3d(my.quart23d(p.gc2),col=3,size=5)
points3d(my.quart23d(h1),col=4,size=10)
points3d(my.quart23d(h2),col=5,size=10)
points3d(my.quart23d(h3),col=2,size=10)

# h1-h2角がh1-h3角より小さいことを確認
for(i in 1:1000){
	h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))

h3 <- h1 * h2

h3 <- my.3d2quart(my.rsphere(1))
#h1 <- Hi*1
#h2 <- Hj*1
#h3 <- Hk*1
p <- my.circle.3pt.check(h1,h2,h3)
p.gc <- my.circle.on.sph(p)

}
  • 球面上の三角形とは、この「球面弧」がタンデムに３つ並んで閉じたもののこと
  • さらに球面上の三角形について向きを考慮に入れるとは、３弧の向きに整合性を入れ、その整合性のとれた向きに意味を持たせた上で、３球面弧の並び方によって定まるもののこと
  • 球面に初めに３角形を多く時には、その３頂点をh1,h2,h3とすれば、h1->h2->h3と、h1->h3->h2という二つの三角形ができる。
  • 球面三角形を定義するには…
my.tri.sphere <- function(h1,h2,h3){
	a1 <- my.circle.3pt(h1,h2)
	a2 <- my.circle.3pt(h1,h2)
	a3 <- my.circle.3pt(h1,h2)
	list(a1=a1,a2=a2,a3=a3)
}
h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))
h3 <- my.3d2quart(my.rsphere(1))

tri.1 <- my.tri.sphere(h1,h2,h3)
  • 三角形の内外判定は、点と回転軸のなす角が辺上の点と回転軸のなす角より大きいか小さいかを３辺(３弧)について実施し、すべてで「より小さい」なら内部、それ以外は外部

my.tri.sphere <- function(h1,h2,h3){
	a1 <- my.circle.3pt(h1,h2)
	a2 <- my.circle.3pt(h2,h3)
	a3 <- my.circle.3pt(h3,h1)
	list(a1=a1,a2=a2,a3=a3)
}

my.check.inside <- function(v,tri){
	ret <- matrix(0,length(v),length(tri))
	for(i in 1:length(tri)){
		tmp.v <- tri[[i]]$v
		tmp.h <- tri[[i]]$start
		tmp.ip <- -Re(tmp.v * tmp.h)
		current.ip <- -Re(tmp.v * v)
		ret[,i] <- sign(current.ip)
	}
	ret
}
R <- my.rsphere(100000)
h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))
h3 <- my.3d2quart(my.rsphere(1))

tri.1 <- my.tri.sphere(h1,h2,h3)

inout <- my.check.inside(my.3d2quart(R),tri.1)
insides <- apply((inout-1)^2,1,sum)

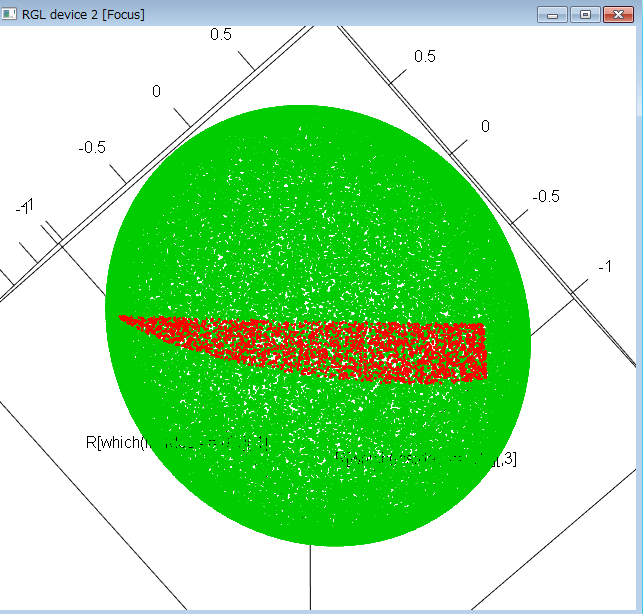
plot3d(R[which(insides==0),],col=2)
points3d(R[which(insides!=0),],col=3)
  • 球面三角形の内側判定が今一つうまく行かないが、仮のソース
library(onion)
library(rgl)

my.rsphere <- function(n){
	ret <- matrix(rnorm(n*3),ncol=3)
	ret/sqrt(apply(ret^2,1,sum))
}

my.3d2quart <- function(x){
	if(is.vector(x)){
		x <- matrix(x,nrow=1)
	}
	x[,1] * Hi + x[,2] * Hj + x[,3] * Hk
}
my.quart23d <- function(h){
	t(as.matrix(Im(h))[2:4,])
}
my.greatcircle <- function(h1,h2){
	h3 <- -h1 * h2
	theta <- acos(-Re(h3))
	
	list(v=Im(h3),theta=theta,start=h1,end=h2)
}

my.circle.3pt.check <- function(h1,h2,h3){
	# 三角形の２辺。向きも考慮
	h12 <- h2-h1
	h23 <- h3-h2
	# ３頂点ベクトルと回転軸ベクトルのなす角が等しいことを利用して、
	# ２辺ベクトルと回転軸ベクトルの内積が0であることを条件に回転軸ベクトルを算出
	# 回転軸ベクトルの和は、仮に１とする
	M <- matrix(c(i(h12),j(h12),k(h12),i(h23),j(h23),k(h23),1,1,1),byrow=TRUE,3,3)
	if(det(M)!=0){
		a <- c(0,0,1)
		# 回転軸ベクトルを単位ベクトル化し
		tmp <- solve(M,a)
		tmp <- tmp/sqrt(sum(tmp^2))
		v <- (Hi*tmp[1] + Hj*tmp[2] + Hk*tmp[3])
		# 向きを考慮した２辺のベクトル積と回転軸ベクトルの内積が負であるなら
		# 回転軸ベクトルの向きを反転させる
		if(-Re(v * (h12*h23)) < 0){
			 v <- Conj(v)
		}
		
		# 回転角を出すために以下をする
		# ３頂点と回転中心との結ぶベクトルの単位ベクトル(回転平面ベクトル)を作る
		h1.tan <- h1 + Re(v*h1)*v
		h2.tan <- h2 + Re(v*h2)*v
		h3.tan <- h3 + Re(v*h3)*v
		h1.tan <- h1.tan/Mod(Im(h1.tan))
		h2.tan <- h2.tan/Mod(Im(h2.tan))
		h3.tan <- h3.tan/Mod(Im(h3.tan))
		
		# 回転平面ベクトルのベクトル積と内積を使う
		h1h3 <- h1.tan*h3.tan
		h1h2 <- h1.tan*h2.tan
		
		# 回転平面上での頂点v1-v3、v1-v2の角を求める
		theta <- acos(-Re(h1h3))
		theta2 <- acos(-Re(h1h2))


		#re.h1h3 <- Re(h1h3)
		re.h1h2 <- Re(h1h2)
		# 回転平面ベクトルのベクトル積と回転軸ベクトルの内積(方向が同じ傾向か否か)の判定
		tq.h1h3 <- -Re(h1h3*v)
		tq.h1h2 <- -Re(h1h2*v)
		
		# 反時計回りの角に直すための修正
		if(tq.h1h3 < 0){
			theta <- 2*pi-theta
		}
		if(tq.h1h2 < 0){
			theta2 <- 2*pi-theta2
		}
		print(theta-theta2)
		#if(theta < theta2){
		#	v <- Conj(v)
		#	theta <- 2*pi - theta
		#	theta2 <- 2*pi - theta2
		#}
		p <- list(v=v,theta=theta,start=h1,end=h3)
	}else{
		# ３点が大円上に乗っているなら、大円情報を返す
		p <- my.greatcircle(h1,h3)
	}
	p
}
my.circle.3pt <- function(h1,h2,h3=h2){# h3を与えなければh1,h2の大円弧
	# 三角形の２辺。向きも考慮
	h12 <- h2-h1
	h23 <- h3-h2
	# ３頂点ベクトルと回転軸ベクトルのなす角が等しいことを利用して、
	# ２辺ベクトルと回転軸ベクトルの内積が0であることを条件に回転軸ベクトルを算出
	# 回転軸ベクトルの和は、仮に１とする
	M <- matrix(c(i(h12),j(h12),k(h12),i(h23),j(h23),k(h23),1,1,1),byrow=TRUE,3,3)
	if(det(M)!=0){
		a <- c(0,0,1)
		# 回転軸ベクトルを単位ベクトル化し
		tmp <- solve(M,a)
		tmp <- tmp/sqrt(sum(tmp^2))
		v <- (Hi*tmp[1] + Hj*tmp[2] + Hk*tmp[3])
		# 向きを考慮した２辺のベクトル積と回転軸ベクトルの内積が負であるなら
		# 回転軸ベクトルの向きを反転させる
		if(-Re(v * (h12*h23)) < 0){
			 v <- Conj(v)
		}
		
		# 回転角を出すために以下をする
		# ３頂点と回転中心との結ぶベクトルの単位ベクトル(回転平面ベクトル)を作る
		h1.tan <- h1 + Re(v*h1)*v
		h3.tan <- h3 + Re(v*h3)*v
		h1.tan <- h1.tan/Mod(Im(h1.tan))
		h3.tan <- h3.tan/Mod(Im(h3.tan))
		
		# 回転平面ベクトルのベクトル積と内積を使う
		h1h3 <- h1.tan*h3.tan
		
		# 回転平面上での頂点v1-v3、v1-v2の角を求める
		theta <- acos(-Re(h1h3))

		# 回転平面ベクトルのベクトル積と回転軸ベクトルの内積(方向が同じ傾向か否か)の判定
		tq.h1h3 <- -Re(h1h3*v)
		
		# 反時計回りの角に直すための修正
		if(tq.h1h3 < 0){
			theta <- 2*pi-theta
		}
		p <- list(v=v,theta=theta,start=h1,end=h3)
	}else{
		# ３点が大円上に乗っているなら、大円情報を返す
		p <- my.greatcircle(h1,h3)
	}
	p
}

my.circle.on.sph <- function(p,n=100,mint=0,maxt=1){
	t <- seq(from=mint,to=maxt,length=n)
	theta. <- p$theta*t
	q <- cos(theta./2) + sin(theta./2) * (p$v)
	q * p$start * Conj(q)
}


R <- my.rsphere(5000)

h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))

h3 <- h1 * h2

h3 <- my.3d2quart(my.rsphere(1))
#h1 <- Hi*1
#h2 <- Hj*1
#h3 <- Hk*1
p <- my.circle.3pt(h1,h2,h3)
p.gc <- my.circle.on.sph(p)
p.gc2 <- my.circle.on.sph(p,maxt=1000)
plot3d(R)

points3d(my.quart23d(p.gc),col=2,size=5)
points3d(my.quart23d(p.gc2),col=3,size=5)
points3d(my.quart23d(h1),col=4,size=10)
points3d(my.quart23d(h2),col=5,size=10)
points3d(my.quart23d(h3),col=2,size=10)

# h1-h2角がh1-h3角より小さいことを確認
for(i in 1:100){
	h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))

h3 <- h1 * h2

h3 <- my.3d2quart(my.rsphere(1))
#h1 <- Hi*1
#h2 <- Hj*1
#h3 <- Hk*1
p <- my.circle.3pt.check(h1,h2,h3)
p.gc <- my.circle.on.sph(p)

}



my.tri.sphere.old <- function(h1,h2,h3){
	a1 <- my.circle.3pt(h1,h3,h2)
	a2 <- my.circle.3pt(h2,h3)
	a3 <- my.circle.3pt(h3,h1)
	list(a1=a1,a2=a2,a3=a3)
}
my.tri.sphere <- function(h1,h2,h3){
	tmp <- my.circle.3pt(h1,h2,h3)
	tmp2 <- my.circle.3pt(h2,h3,h1)
	tmp3 <- my.circle.3pt(h3,h1,h2)
	a1 <- list(v=tmp$v,theta=2*pi-tmp2$theta,start=h1,end=h2)
	a2 <- list(v=tmp$v,theta=2*pi-tmp3$theta,start=h2,end=h3)
	a3 <- list(v=tmp$v,theta=2*pi-tmp$theta,start=h3,end=h1)
	list(a1=a1,a2=a2,a3=a3)
}

my.check.inout <- function(v,tri){
	ret <- matrix(0,length(v),length(tri))
	for(i in 1:length(tri)){
		#tmp <- (v-tri[[i]]$start) * (v-tri[[i]]$end)
		tmp.v <- tri[[i]]$v
		tmp.h <- tri[[i]]$start
		tmp.ip <- -Re(tmp.v * tmp.h)
		current.ip <- -Re(tmp.v * v)
		ret[,i] <- sign(current.ip-tmp.ip)
		#ret[,i]  <- sign(-Re(tmp * tmp.v))
	}
	ret
}
my.check.inout.ng <- function(v,tri){
	tmp <- (tri[[1]]$end-tri[[1]]$start) * (tri[[3]]$start - tri[[3]]$end)
	ctr <- (tri[[1]]$start+tri[[2]]$start+tri[[3]]$start)/3
	
	sign(Re(tmp * v-ctr))
	
}
my.check.inside.ng <- function(v,tri){
	inout <- my.check.inout(v,tri)
	which(inout>0)
}
my.check.inside <- function(v,tri){
	inout <- my.check.inout(v,tri)
	insides <- apply((inout-1)^2,1,sum)
	which(insides==0)
}

my.arc.inv <- function(a){
	ret <- list(v=Conj(a$v),theta=a$theta,start=a$end,end=a$start)
}
R <- my.rsphere(100000)
h1 <- my.3d2quart(my.rsphere(1))
h2 <- my.3d2quart(my.rsphere(1))
h3 <- my.3d2quart(my.rsphere(1))


h1 <- Hi
h2 <- Hj
h3 <- Hk

tri.1 <- my.tri.sphere(h1,h2,h3)
tri.2 <- my.tri.sphere(h1,h3,h2)
inout <- my.check.inout(my.3d2quart(R),tri.1)
inout2 <- my.check.inout(my.3d2quart(R),tri.2)
insides <- apply((inout-1)^2,1,sum)

ins <- my.check.inside(my.3d2quart(R),tri.1)
ins2 <- my.check.inside(my.3d2quart(R),tri.2)

plot3d(R[ins,],col=2)
points3d(R[-ins,],col=3)

plot3d(R[which(insides==0),],col=2)
points3d(R[which(insides!=0),],col=3)


my.arc.length <- function(p){
		tmp.v <- p$v
		tmp.h <- p$start
		tmp.ip <- -Re(tmp.v * tmp.h)
		h <- tmp.h - tmp.ip*tmp.v
		p$theta * Mod(h)
}
my.make.euler.tri <- function(n,m=1000){
	tris <- list()
	h.three <- my.3d2quart(my.rsphere(3))
	col <- c(1,2)
	tris[[1]] <- my.tri.sphere(h.three[1],h.three[2],h.three[3])
	tris[[2]] <- my.tri.sphere(h.three[1],h.three[3],h.three[2])
	for(i in 2:n){
		select.tri <- sample(1:length(tris),1)
		selected.tri <- tris[[select.tri]]
		selected.col <- col[select.tri]
		loop <- TRUE
		while(loop){
			R <- my.3d2quart(my.rsphere(m))
			#inout <- my.check.inout(R,selected.tri)
			#insides <- apply((inout-1)^2,1,sum)
			ins <- my.check.inside(R,selected.tri)
			if(length(ins)>1){
				ss <- sample(ins,2)
				tmp1 <- R[ss[1]]
				tmp2 <- R[ss[2]]
				loop <- FALSE
				select.arc <- sample(1:3,1)
				selected.arc <- selected.tri[[select.arc]]
				st <- selected.arc$start
				ed <- selected.arc$end
				circle1 <- my.tri.sphere(st,tmp1,ed)
				circle2 <- my.tri.sphere(st,tmp2,ed)
				a1st <- circle1$a1
				a1ed <- circle1$a2
				a2st <- circle2$a1
				a2ed <- circle2$a2
				a1st.len <- my.arc.length(a1st)
				a1ed.len <- my.arc.length(a1ed)
				a2st.len <- my.arc.length(a2st)
				a2ed.len <- my.arc.length(a2ed)
				outer <- tmp1
				inner <- tmp2
				if(a1st.len + a1ed.len < a2st.len + a2ed.len){
					outer <- tmp2
					inner <- tmp1
				}
				#new.a1 <- my.circle.3pt(st,outer,ed)
				#new.a1.opposit <- my.circle.3pt(ed,outer,st)
				#new.a2 <- my.circle.3pt(st,inner)
				#new.a2.opposit <- my.circle.3pt(st,inner)
				#new.a3 <- my.circle.3pt(inner,ed)
				#new.a3.opposit <- my.circle.3pt(inner,ed)
				new.a1 <- my.circle.3pt(st,outer,ed)
				a2 <- my.tri.sphere(ed,inner,st)
				old.a <- tris[[select.tri]][[select.arc]]
				
				
				tris[[select.tri]][[select.arc]] <- new.a1
				new.tri1 <- list(a1=my.arc.inv(a2$a1),a2=my.arc.inv(a2$a1),a3=my.arc.inv(a2$a2))
				new.tri2 <- list(a1=old.a,a2=a2$a1,a3=a2$a2)
				n.tri <- length(tris)
				tris[[n.tri+1]] <- new.tri1
				tris[[n.tri+2]] <- new.tri2
				if(selected.col==1){
					col[n.tri+1] <- 2
					col[n.tri+2] <- 1
				}else{
					col[n.tri+1] <- 1
					col[n.tri+2] <- 2
				}
			}
		}
	}
	list(tris=tris,col=col)
}


my.plot.euler.tri <- function(tris,col,n=10000){
	R <- my.3d2quart(my.rsphere(n))
	x <- matrix(0,n,length(tris))
	for(i in 1:length(tris)){
		tmp.ins <- my.check.inside(R,tris[[i]])
		x[tmp.ins,i] <- 1
	}
	#x
	R3d <- my.quart23d(R)
	#plot3d(R3d,col=gray(0.1))
	for(i in 1:length(tris)){
		if(i==1){
			plot3d(R3d[which(x[,i]==1),],col=i+1)
		}
		points3d(R3d[which(x[,i]==1),],col=i+1)
	}
	x
}
ttt <- my.make.euler.tri(6)

apply(x,1,sum)


for(i in 1:length(ttt$tris)){
	for(j in 1:3){
		print(ttt$tris[[i]][[j]]$start)
		print(ttt$tris[[i]][[j]]$end)
	}
}

ttt <- my.make.euler.tri(20)

tmpout <- my.plot.euler.tri(ttt$tris,ttt$col,n=100000)