遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

barycentric coordinates

barycentric coordinates R 射影 単体
  • 平面に三角形があるとする。平面上の点なので、2次元デカルト座標で表すこともできるが、barycentric coordinatesでは、３点のベクトルに足して１になるように重みづけをして３ベクトルの線形和がその点の位置を表すように、3つの数(足して１の制約があるので自由度２)の重みづけベクトルを座標として用いる
  • それを単体に拡張することも容易である。(さらに単体でなく多面体版に拡張することもあるらしい
  • Wikipediaはこちら
  • その座標の求め方として、三角形を例にとる
    • 3点のうち1点を基準点として原点とみなせば、残りの2点は線形独立な２つのベクトル。この２つのベクトルの線形和となるように係数を決める。その２つの係数の和が１ならば、２つのベクトルの頂点を結んだ直線上の点となるし、１より小さければ、原点とした頂点に近い値となる。実際、１より小さい分を原点扱いの頂点の係数とすれば、３係数の和が１となっていて、３ベクトルの線形和として表すことができる
  • これをすると、任意次元の単体を取ったとき、その空間の点を1次元ずつ下げつつ、減次元単体に射影して行って、最終的にある辺の上の一点にまで対応づけることができる
  • この話と、先日来の高次元の複比問題がつながるのでは、という話
  • どうつながるかというと、今、多次元空間において、行列の指数関数的な軌道があるとき、多次元から2次元を取り出せば、その二次元に関して１次元射影空間に写像すれば複比が保存されるのだが、barycentric coordinatesを使って、そのような1次元射影空間にマップしてやれば、あっちでもこっちでも複比が保存されながら動く、というようなそんな状況になるのでは、ということ…
  • ひとまず、barycentric coordinatesを扱いつつ、任意の辺に写像するためのR関数を準備する

# d : dimension
# z : d x (d+1) matrix
# x : d vector
# d+1頂点座標をd+1列に持つ行列zについて、右端のベクトルから順に原点扱いしつつ、barycentric coordinatesを計算するとともに、原点と向かい合う減次元単体に写像する
# その係数と写像のデカルト座標を記録して行き、返す
my.projection.simplex.edge <- function(x,z){
	d <- length(z[,1])
	coef.list <- coef.list.st <- bary.list <- list()
	xs.map <- xs.map2 <- matrix(0,d,d)
	xs.map[1,] <- xs.map2[1,] <- x
	coef.list[[1]] <- coef.list.st[[1]] <- c()
	for(i in 2:(d)){
		d. <- d-i+2
		zero <- z[,d.+1]
		tmp.z <- z[1:d.,1:d.]
		tmp.z.2 <- tmp.z - zero[1:d.]
		tmp.x <- xs.map[i-1,1:d.] - zero[1:d.]
		coef.list[[i]] <- solve(tmp.z.2) %*% tmp.x
		bary.list[[i]] <- c(coef.list[[i]],1-sum(coef.list[[i]]))
		coef.list.st[[i]] <- coef.list[[i]]/sum(coef.list[[i]])
		xs.map[i,] <- (z[,1:d.]-zero) %*% coef.list.st[[i]] + zero
		xs.map2[i,] <- z[,1:(d.+1)] %*% bary.list[[i]]
	}
	return(list(xs.map=xs.map,xs.map2=xs.map2,coef.list=coef.list,coef.list.st=coef.list.st,bary.list = bary.list))
}
# 適当に点を取り、やってみる
d <- 3
z <- matrix(rnorm(d*(d+1)),d,d+1)
# 正単体内部の乱点を発生させる
library(MCMCpack)
n.iter <- 1000
R <- rdirichlet(n.iter,rep(1,d+1))
xx <- matrix(0,0,3)

for(i in 1:n.iter){
#x <- rnorm(d)
x <- z %*% R[i,]
mpse <- my.projection.simplex.edge(x,z)
xx <- rbind(xx,mpse$xs.map)
}
library(rgl)
plot3d(t(z),col=1,size=5)
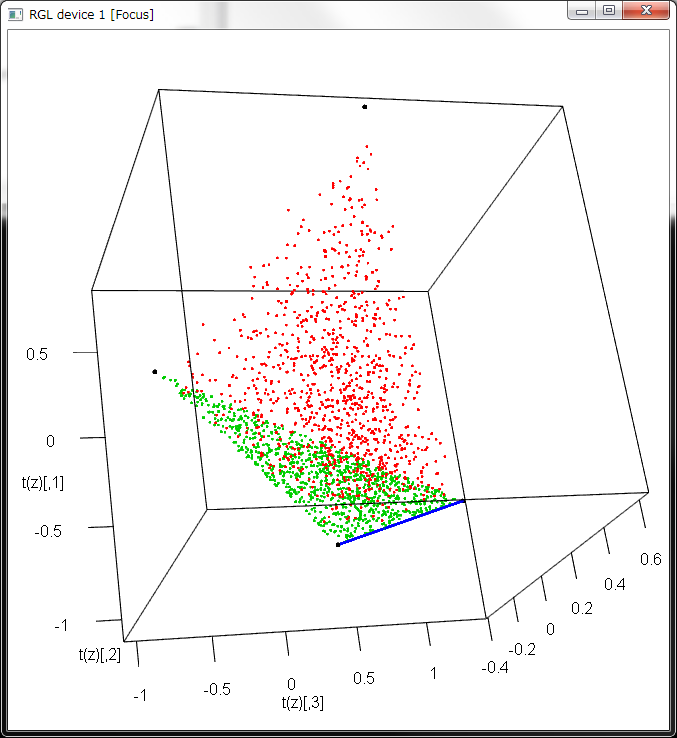
points3d(xx,col=rep(2:(d+1),n.iter))
  • 確かに、段階が進むにつれ(色で区別)、正単体→減次元正単体→…→辺へと写像が移行する様子がわかる
  • さて。行列の指数関数変化をしている点の射影空間写像について、これをやってみる。確かに、各辺で複比が保存されているかを見てみよう
# 行列の指数関数
exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
# 複比計算
my.doubleratio <- function(x){
	if(!is.matrix(x)){
		x <- matrix(x,nrow=length(x))
	}
	P <- x[1:(length(x[,1])-3),]
	Q <- x[4:length(x[,1]),]
	S <- x[2:(length(x[,1])-2),]
	R <- x[3:(length(x[,1])-1),]
	((P-R)/(Q-R))/((P-S)/(Q-S))
}

# d次元射影空間に対応するd+1変数の連立常微分方程式
d <- 4
# なんでも良いはずだが、きれいなカーブになるように、上微分方程式の行列を作る
library(GPArotation)
R <- Random.Start(d+1)
lambdas <- runif(d+1)
A <- R %*% diag(lambdas) %*% t(R)

eigen.out <- eigen(A)
S <- eigen.out[[2]]
S. <- t(t(S)/S[d+1,])
library(MCMCpack)
coef.init <- rdirichlet(1,rep(1,d+1))
X.init <- rep(0,d+1)
for(i in 1:(d+1)){
	X.init <- X.init + coef.init[i] * S.[,i]
}
t <- seq(from=-10,to=10,length=300)
X <- matrix(0,length(t),length(A[,1]))
for(i in 1:length(t)){
	X[i,] <- Re(exp.m(A,t[i])[[1]] %*% X.init)
}
# 射影する
X. <- X/X[,d+1]

#plot(Re(t(S.[1:2,])),asp=TRUE)
plot(Re(t(S.[1:2,])))
points(X.[,1:2],type="l",col=2)
for(i in 1:(d)){
	for(j in (i+1):(d+1)){
	next.i <- j
	if(next.i > d+1){
		next.i <- 1
	}
	segments(S.[1,i],S.[2,i],S.[1,next.i],S.[2,next.i],col=4)
	}
}
# さて。射影空間において、頂点座標がわかっているものとして、各辺へと写像しよう
Xs <- X.[,1:d]
Zs <- S.[1:d,]
# すべての辺を列挙
ed <- combn(1:(d+1),2)
ys <- matrix(0,length(Xs[,1]),length(ed[1,]))

for(i in 1:length(Xs[,1])){
	for(j in 1:length(ed[1,])){
# 正単体の頂点の順序を変えて、写像先である辺を取りかえる
		tmp.Zs <- Zs[,c(ed[,j],(1:(d+1))[-ed[,j]])]
	tmp <- my.projection.simplex.edge(Xs[i,],tmp.Zs)
	coef.list.st <- tmp$coef.list.st
	ys[i,j] <- coef.list.st[[length(coef.list.st)]][1]
	}
}
# 各辺への写像について複比を調べる
my.doubleratio(ys)
  • 三角形の頂点に３つの値を定め、辺には両端の頂点の値の重みをつけた点を取り、その点とその点を含む辺と対になっている頂点を結ぶと1点で交わることを示しておこう
tri <- matrix(rnorm(6),3,2)

lambdas <- runif(3)

plot(tri,asp=TRUE)

for(i in 1:3){
	i2 <- i+1
	if(i2>3){
		i2 <- 1
	}
	tmp <- (lambdas[i] * tri[i,] + lambdas[i2] * tri[i2,])/(lambdas[i]+lambdas[i2])
	
	op.v <- (1:3)[-c(i,i2)]
	segments(tri[op.v,1],tri[op.v,2],tmp[1],tmp[2])
	segments(tri[i,1],tri[i,2],tri[i2,1],tri[i2,2],col=2)
}