2013-05-19

多次元球のいろいろな張り合わせ

多次元視覚のことをやっている(こちら)
そうすると、視覚で取った情報から各点の微分に関する情報を取り出して、それによって対象を理解しようか、という話になる
じゃあ、ということで多様体上の微分のことが気になるのだが、そこには「球は球でも微分の状態が違うことがある」という話題がある
エキゾチックな球面という話である(こちら)
多次元球面ならどんなものでもエキゾチックな球面があるかというとそうでもないらしい
歴史的に最初に登場した７次元球面の話でこれをなぞってみることにする(７次元のエキゾチック球面)
５次元空間 $\mathbf{R}^5$ の球面 $S4$ ; $(x_1,x_2,...,x_5);\sum_{i=1}^5 x_i^2=1$ と４次元空間 $\mathbf{R}^4$ の球面 $S3$ ; $(y_1,y_2,...,y_4);\sum_{j=1}^4 y_i^2=1$ とを考える
$S4 \times S3$ という直積空間は、 $S4$ , $S3$ 上の点のペアのすべてを網羅する空間。自由度4+3=7
ここでは $z=(\mathbf{x},\mathbf{y});\sum_{i=1}^{5+4} z_i^2 =2$ となっている
さて。
$S4$ を $x_5=0$ という赤道でその上半分 $S4_{x_5 > 0}$ と下半分 $S4_{x_5 < 0}$ に分けることにする
この切り口は $\sum_{i=1}^4 x_i^2=1$ なる球面である。上で述べた $S3$ と区別するべく $S3_0$ と書くことにする
この切り口 $S3_0$ に対応する直積空間 $S3_0 \times S3$ があるから、 $S4$ の赤道で切り離すというときには直積空間全体を２分割している
切り離したら、つなぎたい(貼りあわせなおしたい)
貼りなおすときには上半分と下半分とが「きれいに１対１対応」するようにすることを考える
切り口のすべての点の対応関係を４元数を使ってうまいことやろう、という話
$(x_1,x_2,x_3,x_4,y_1,y_2,y_3,y_4)$ という８つの数( $x_5=0$ であるので除いてある)を４つと４つ( $(x_1,x_2,x_3,x_4),(y_1,y_2,y_3,y_4)$ に分けて、それを $x_1 + i x_2 + j x_3 + k x_4$ というような四元数に対応付けよう。 $q(x),q(y)$ としよう
$q(x),q(y)$ のノルムは１
今、四元数の性質から、q(x),q(y)のハミルトニアン積 $q(x)q(y)$ もやはり四元数でそのノルムが１だから
上半分の $(x,y)$ と下半分の $(x,y')$ (ただし $y'$ はハミルトニアン積( $q(x)q(y)$ の４成分の係数が作る長さ４のベクトルとする)が１対１対応付けできる
(その貼りあわせも素直な対応関係だから微分可能で、そうすると、微分の仕方の違う球面ができる、という話)
Rでやってみよう。Rには四元数・八元数をハンドリングするonionパッケージがある(ハミルトニアン積の関数がどれだか分らなかったのであまりメリットを得ていないのだが…)
適当に回転させてその軌道が貼り合わせによって変わることをみる

install.packages("onion")
library(onion)
# ばらばらとした小さな回転角の回転行列を作る(カッコ悪い出来になっている)
Small.Rotation <- function(d,n.iter=100,r=0.01){
	R <- diag(rep(1,d))
	for(i in 1:n.iter){
		s <- sample(1:d,2)
		t <- rnorm(1) * r
		tmp.R <- diag(rep(1,d))
		tmp.R[s[1],s[1]] <- tmp.R[s[2],s[2]] <- cos(t)
		tmp.R[s[1],s[2]] <- -sin(t)
		tmp.R[s[2],s[1]] <- sin(t)
		R <- tmp.R %*% R
	}
	R
}
# 四元数のハミルトン積
Hamiloton.prod.quat <- function(u,v){
	x <- Re(u)*Re(v)-i(u)*i(v) -j(u)*j(v)-k(u)*k(v)
	y <- Re(u)*i(v)+i(u)*Re(v)+j(u)*k(v)-k(u)*j(v)
	z <- Re(u)*j(v)-i(u)*k(v)+j(u)*Re(v)+k(u)*i(v)
	w <- Re(u)*k(v)+i(u)*j(v)-j(u)*i(v)+k(u)*Re(v)
	quaternion(Re=x,i=y,j=z,k=w)
}
# S4,S3のそれぞれの座標を作る
d5 <- 5
d4 <- 4
# 回転しながらn.pt個の点を作る
d5 <- 5
d4 <- 4
n.pt <- 1000
X5 <- matrix(0,n.pt,d5)
X4 <- matrix(0,n.pt,d4)
X5[1] <- X4[1] <- 1
X5.ori <- X5
X4.ori <- X4
# 貼りあわせを越えたときに１を立てる
hariawase <- rep(0,n.pt)

# 回転行列
R5 <- Small.Rotation(d5)
R4 <- Small.Rotation(d4)

# 1点1点作る
for(i in 2:n.pt){
# 仮に回転後の座標を作る
	tmp5 <- R5 %*% X5[i-1,]
	tmp4 <- R4 %*% X4[i-1,]
# 貼り合わせを越えるとは第５成分の正負が替わることなのでそれを判定
	if(tmp5[5] * X5[i-1,5] < 0){
# 二つの四元数を作る
		hariawase[i] <- 1
		tmp.u <- tmp5
# 四元数のノルムが１であるときに貼りあわせるのでそのためにちょっと調整する
		tmp.u <- tmp.u/sqrt(sum(tmp5[1:4]^2))
		u <- quaternion(Re=tmp.u[1],i=tmp.u[2],j=tmp.u[3],k=tmp.u[4])
		v <- quaternion(Re=tmp4[1],i=tmp4[2],j=tmp4[3],k=tmp4[4])
		uv <- Hamiloton.prod.quat(u,v)
		#tmp.X5 <- c(X5[i-1,1:4],-X5[i-1,5])
		#tmp.X4 <- c(Re(uv),i(uv),j(uv),k(uv))
		X5[i,] <- tmp5
		X4[i,] <- c(Re(uv),i(uv),j(uv),k(uv))

	}else{# 乗り越えてない
		X5[i,] <- tmp5
		X4[i,] <- tmp4
	}
# 変な張り合わせでなければ普通に回転行列を作用させるだけ
	X5.ori[i,] <- R5 %*% X5.ori[i-1,]
	X4.ori[i,] <- R4 %*% X4.ori[i-1,]

}
# 回転の様子をペアワイズプロットで見る
plot(as.data.frame(cbind(X5,X4)),cex=0.01)
plot(as.data.frame(cbind(X5.ori,X4.ori)),cex=0.01)
# 回転の様子をmatplot()で見る
matplot(cbind(X5,X4),type="l")
matplot(cbind(X5.ori,X4.ori),type="l")
# 貼りあわせの仕方の違いがどう表れるかを見る
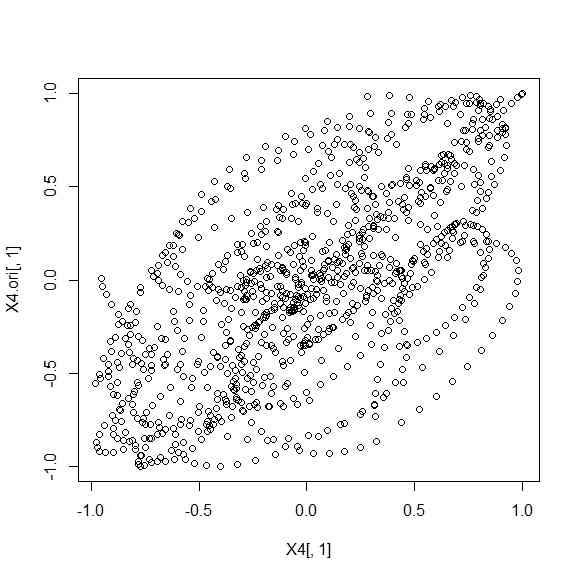
plot(X5[,1],X5.ori[,1])
plot(X4[,1],X4.ori[,1])