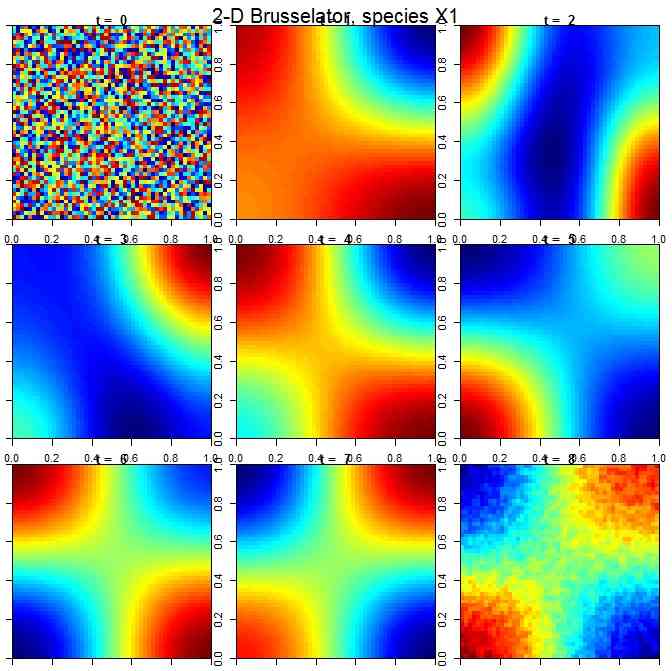
diffEqパッケージで数値微分

• こちらのPDFをただコピーして実行してみるだけ

Solving Differential Equations in R (Use R!)

• この本の１０章の話

library(diffEq)
N <- 100
xgrid <- setup.grid.1D(x.up = 0, x.down = 1, N = N)
x <- xgrid$x.mid
D.coeff <- 0.01
Diffusion <- function (t, Y, parms){
tran <- tran.1D(C = Y, C.up = 0, C.down = 1,
D = D.coeff, dx = xgrid)
list(dY = tran$dC, flux.up = tran$flux.up,
flux.down = tran$flux.down)
}
Yini <- sin(pi*x)
times <- seq(from = 0, to = 5, by = 0.01)
print(system.time(
out <- ode.1D(y = Yini, times = times, func = Diffusion,
parms = NULL, dimens = N) ))
par (mfrow=c(1, 2))
plot(out[1, 2:(N+1)], x, type = "l", lwd = 2,xlab = "Variable, Y", ylab = "Distance, x")
for (i in seq(2, length(times), by = 50))
lines(out[i, 2:(N+1)], x)
image(out, grid = x, mfrow = NULL, ylab = "Distance, x",main = "Y")


dx <- 0.2
xgrid <- setup.grid.1D(x.up = -100, x.down = 100, dx.1 = dx)
x <- xgrid$x.mid
N <- xgrid$N
lam <- 0.05
uini <- exp(-lam*x^2)
vini <- rep(0, N)
yini <- c(uini, vini)
times <- seq (from = 0, to = 50, by = 1)
wave <- function (t, y, parms) {
u <- y[1:N]
v <- y[(N+1):(2*N)]
du <- v
dv <- tran.1D(C = u, C.up = 0, C.down = 0, D = 1,
dx = xgrid)$dC
return(list(c(du, dv)))
}
out <- ode.1D(func = wave, y = yini, times = times,
parms = NULL, method = "adams",
dimens = N, names = c("u", "v"))
u <- subset(out, which = "u")
analytic <- function (t, x)
0.5 * (exp(-lam * (x+1*t)^2 ) +exp(-lam * (x-1*t)^2) )
OutAna <- outer(times, x, FUN = analytic)
max(abs(u - OutAna))
outtime <- seq(from = 0, to = 50, by = 10)
matplot.1D(out, which = "u", subset = time %in% outtime,
grid = x, xlab = "x", ylab = "u", type = "l",
lwd = 2, xlim = c(-50, 50),
col = c("black", rep("darkgrey", 5)))
legend("topright", lty = 1:6, lwd = 2,
col = c("black", rep("darkgrey", 5)),
title = "t = ", legend = outtime)



Nx <- 100
Ny <- 100
xgrid <- setup.grid.1D (x.up = 0, x.down = 1, N = Nx)
ygrid <- setup.grid.1D (x.up = 0, x.down = 1, N = Ny)
x <- xgrid$x.mid
y <- ygrid$x.mid
laplace <- function(t, U, parms) {
w <- matrix(nrow = Nx, ncol = Ny, data = U)
dw <- tran.2D(C = w, C.x.up = 0, C.x.down = 0,
flux.y.up = 0,
flux.y.down = -1 * sin(pi*x)*pi*sinh(pi),
D.x = 1, D.y = 1,
dx = xgrid, dy = ygrid)$dC
list(dw)
}
print(system.time(
out <- steady.2D(y = runif(Nx*Ny), func = laplace,
parms = NULL, nspec = 1,
dimens = c(Nx, Ny), lrw = 1e7)
))
w <- matrix(nrow = Nx, ncol = Ny, data = out$y)
analytic <- function (x, y) sin(pi*x) * cosh(pi*y)
OutAna <- outer(x, y, FUN = analytic)
max(abs(w - OutAna))
image(out, grid = list(x, y), main = "elliptic Laplace",
add.contour = TRUE)



adv.func <- function(t, y, p, adv.method)
list(advection.1D(C = y, C.up = y[N], C.down = y[1],
v = 0.1, adv.method = adv.method,
dx = xgrid)$dC)
xgrid <- setup.grid.1D(0.3, 1.3, N = 50)
x <- xgrid$x.mid
N <- length(x)
yini <- sin(pi * x)^50
times <- seq(0, 20, 0.01)
out1 <- ode.1D(y = yini, func = adv.func, times = times,
parms = NULL, method = "euler", dimens = N,
adv.method = "muscl")
out2 <- ode.1D(y = yini, func = adv.func, times = times,
parms = NULL, method = "euler", dimens = N,
adv.method = "super")


N <- 50
Grid <- setup.grid.1D(x.up = 0, x.down = 1, N = N)
x1ini <- 1 + sin(2 * pi * Grid$x.mid)
x2ini <- rep(x = 3, times = N)
yini <- c(x1ini, x2ini)
brusselator1D <- function(t, y, parms) {
X1 <- y[1:N]
X2 <- y[(N+1):(2*N)]
dX1 <- 1 + X1^2*X2 - 4*X1 +
tran.1D (C = X1, C.up = 1, C.down = 1,
D = 0.02, dx = Grid)$dC
dX2 <- 3*X1 - X1^2*X2 +
tran.1D (C = X2, C.up = 3, C.down = 3,
D = 0.02, dx = Grid)$dC
list(c(dX1, dX2))
}
times <- seq(from = 0, to = 10, by = 0.1)
print(system.time(
out <- ode.1D(y = yini, func = brusselator1D,
times = times, parms = NULL, nspec = 2,
names = c("X1", "X2"), dimens = N)
))
par(mfrow = c(2, 2))
image(out, mfrow = NULL, grid = Grid$x.mid,
which = "X1", method = "contour")
image(out, mfrow = NULL, grid = Grid$x.mid,
which = "X1")
par(mar = c(1, 1, 1, 1))
image(out, mfrow = NULL, grid = Grid$x.mid,
which = "X1", method = "persp", col = NA)
image(out, mfrow = NULL, grid = Grid$x.mid,
which = "X1", method = "persp", border = NA,
shade = 0.3 )



brusselator2D <- function(t, y, parms) {
X1 <- matrix(nrow = Nx, ncol = Ny,
data = y[1:(Nx*Ny)])
X2 <- matrix(nrow = Nx, ncol = Ny,
data = y[(Nx*Ny+1) : (2*Nx*Ny)])
dX1 <- 1 + X1^2*X2 - 4*X1 +
tran.2D (C = X1, D.x = D_X1, D.y = D_X1,
dx = Gridx, dy = Gridy)$dC
dX2 <- 3*X1 - X1^2*X2 +
tran.2D (C = X2, D.x = D_X2, D.y = D_X2,
dx = Gridx, dy = Gridy)$dC
list(c(dX1, dX2))
}
Nx <- 50
Ny <- 50
Gridx <- setup.grid.1D(x.up = 0, x.down = 1, N = Nx)
Gridy <- setup.grid.1D(x.up = 0, x.down = 1, N = Ny)
D_X1 <- 2
D_X2 <- 8*D_X1
X1ini <- matrix(nrow = Nx, ncol = Ny, data = runif(Nx*Ny))
X2ini <- matrix(nrow = Nx, ncol = Ny, data = runif(Nx*Ny))
yini <- c(X1ini, X2ini)
times <- 0:8
print(system.time(
out <- ode.2D(y = yini, parms = NULL, func = brusselator2D,
nspec = 2, dimens = c(Nx, Ny), times = times,
lrw = 2000000, names=c("X1", "X2"))
))
par(oma = c(0,0,1,0))
image(out, which = "X1", xlab = "x", ylab = "y",
mfrow = c(3, 3), ask = FALSE,
main = paste("t = ", times),
grid = list(x = Gridx$x.mid, y = Gridy$x.mid))
mtext(side = 3, outer = TRUE, cex = 1.25, line = -1,
"2-D Brusselator, species X1")


Nr <- 100
Np <- 100
r <- seq(2, 4, len = Nr+1)
theta <- seq(0, 2*pi, len = Np+1)
theta.mid <- 0.5*(theta[-1] + theta[-Np])
Model <- function(t, C, p) {
y = matrix(nrow = Nr, ncol = Np, data = C)
tran <- tran.polar (y, D.r = 1, r = r, theta = theta,
C.r.up = 0, C.r.down = 4 * sin(5*theta.mid),
cyclicBnd = 2)
list(tran$dC)
}
STD <- steady.2D(y = runif(Nr*Np), parms = NULL,
func = Model, dimens = c(Nr, Np),
lrw = 1e6, cyclicBnd = 2)
OUT <- polar2cart (STD, r = r, theta = theta,
x = seq(-4, 4, len = 400),
y = seq(-4, 4, len = 400))
image(OUT, main = "Laplace")



Nx <- 80
Ny <- 80
xgrid <- setup.grid.1D(-7, 7, N=Nx)
ygrid <- setup.grid.1D(-7, 7, N=Ny)
x <- xgrid$x.mid
y <- ygrid$x.mid
sinegordon2D <- function(t, C, parms) {
u <- matrix(nrow = Nx, ncol = Ny,
data = C[1 : (Nx*Ny)])
v <- matrix(nrow = Nx, ncol = Ny,
data = C[(Nx*Ny+1) : (2*Nx*Ny)])
dv <- tran.2D (C = u, C.x.up = 0, C.x.down = 0,
C.y.up = 0, C.y.down = 0,
D.x = 1, D.y = 1,
dx = xgrid, dy = ygrid)$dC - sin(u)
list(c(v, dv))
}
peak <- function (x, y, x0 = 0, y0 = 0)
exp(-((x-x0)^2 + (y-y0)^2))
uini <- outer(x, y,
FUN = function(x, y) peak(x, y, 2,2) + peak(x, y,-2,-2)
+ peak(x, y,-2,2) + peak(x, y, 2,-2))
vini <- rep(0, Nx*Ny)
times <- 0:3
print(system.time(
out <- ode.2D (y = c(uini, vini), times = times,
parms = NULL, func = sinegordon2D,
names = c("u", "v"),
dimens = c(Nx, Ny), method = "ode45")
))


mr <- par(mar = c(0, 0, 1, 0))
image(out, main = paste("time =", times), which = "u",
grid = list(x = x, y = y), method = "persp",
border = NA, col = "grey", box = FALSE,
shade = 0.5, theta = 30, phi = 60, mfrow = c(2, 2),
ask = FALSE)
par(mar = mr)



alf <- 0.5
gam <- 1
Schrodinger <- function(t, u, parms) {
du <- 1i * tran.1D (C = u, D = 1, dx = xgrid)$dC +
1i * gam * abs(u)^2 * u
list(du)
}
N <- 300
xgrid <- setup.grid.1D(-20, 80, N = N)
x <- xgrid$x.mid
c1 <- 1
c2 <- 0.1
sech <- function(x) 2/(exp(x) + exp(-x))
soliton <- function (x, c1)
sqrt(2*alf/gam) * exp(0.5*1i*c1*x) * sech(sqrt(alf)*x)
yini <- soliton(x, c1) + soliton(x-25, c2)
times <- seq(0, 40, by = 0.1)
print(system.time(
out <- ode.1D(y = yini, parms = NULL, func = Schrodinger,
times = times, dimens = 300, method = "adams")
))
user system elapsed
2.18 0.03 2.28
image(abs(out), grid = x, ylab = "x", main = "two solitons")