2014-08-09

射影変換とRANSAC推定法

R 射影変換 RANSCAC推定 Homography

線形変換
- $(x_1,x_2,...,x_n,1)$ という同次座標を線形変換して $(y_1,...,y_n,y_{n+1})$ に写し、これを同次座標とみて、 $(\frac{y_1}{y_{n+1}},\frac{y_2}{y_{n+1}},...\frac{y_n}{y_{n+1}})$ に写せば、結局、n次元座標をn次元座標に写すことになる。
- ここで、この行列と変換の性質について確認する
  - 合同な変換
    - nxn回転行列Rと要素数nのベクトルとを列連結し、第n+1行の1-n列要素は0、n+1要素が1であるような行列
    - 回転行列部分は回転を、tが平行移動を担う
  - 相似な変換
    - 上記の行列のnxn回転行列部分を定数倍したもの
  - Affine変換：等距離だったものが変換後に等距離でなくなり、角度も変わる変換。平行線は平行なまま、平行線の長さの比は保たれる。
    - 上記の行列の回転が楕円的拡大縮小を持つ
  - 射影変換：非線形。Affine変換で保たれていた平行線の関係、平行線上の線分の長さの比が保たれない。射影変換で保たれるのは、同一線上の３点は、変換後も同一線上の点である(もちろん位相も崩れない)
    - 第n+1行の1-n成分が0でなくなる
- 行列をこの指定方式で作ってみる

s <- 2
theta <- pi/3
R <- matrix(c(cos(theta),-sin(theta),sin(theta),cos(theta)),byrow=TRUE,2,2)
v <- runif(3)
v[3] <- 1
#v <- c(0,0,1)
a <- 2
b <- 0.3
U <- matrix(c(a,b,0,1/a),byrow=TRUE,2,2)
t <- c(2,4)


HS <- rbind(matrix(c(s*R,t),2,3),c(0,0,1))
HA <- rbind(matrix(c(U,0,0),2,3),c(0,0,1))
HP <- diag(rep(1,3))
HP[3,] <- v

H <- HS %*% HA %*% HP


# ふつうの格子
t <- seq(from=0,to=1,length=1000)
u <- seq(from=0,to=1,length=10)
tu1 <- expand.grid(t,u)
tu2 <- expand.grid(u,t)
grid1 <- rbind(tu1,tu2)
plot(grid1,pch=20,cex=0.3,main="ふつう")

# 同次

grid1. <- cbind(grid1,rep(1,length(grid1[,1])))
grid2. <- t(H %*% t(grid1.))

grid2 <- grid2.[,1:2]/grid2.[,3]
plot(grid2,pch=20,cex=0.3,main="ふつう射影変換後")

# 指数増加の格子
t <- exp(seq(from=0,to=8,length=1000))
u <- exp(seq(from=0,to=8,length=20))
tu1 <- expand.grid(t,u)
tu2 <- expand.grid(u,t)
grid1 <- rbind(tu1,tu2)
plot(grid1,pch=20,cex=0.3,main="指数増加")

# 同次

grid1. <- cbind(grid1,rep(1,length(grid1[,1])))
grid2. <- t(H %*% t(grid1.))

grid2 <- grid2.[,1:2]/grid2.[,3]
plot(grid2,pch=20,cex=0.3,main="指数増加射影変換後")

ここしばらくやってきている『n+1個の変数の連立微分方程式としてできる軌道の射影変換をして同次座標をとる』ということをやってみる

H <- HS %*% HA %*% HP
n <- 100
# 回転があるから、返還前の座標の第３成分は１にしてある
X <- rbind(exp(0.07*(1:n)),exp(0.05*(1:n)),rep(1,n))
Y <- H %*% X
# 乱雑項を入れる
Y. <- Y + rnorm(length(Y),0,0.1)

plot(t(Y.))
plot(Y[1,],Y[2,])
plot(Y.[1,]/Y.[3,],Y.[2,]/Y.[3,])
Z <- rbind(Y.[1,]/Y.[3,],Y.[2,]/Y.[3,],Y[3,]/Y[3,])
n <- 100
X <- rbind(exp(0.07*(1:n)),exp(0.05*(1:n)),rep(1,n))
Y <- H %*% X
Y. <- Y + rnorm(length(Y),0,0.1)
plot(t(Y.))
plot(Y[1,],Y[2,])
plot(Y.[1,]/Y.[3,],Y.[2,]/Y.[3,])
Z <- rbind(Y.[1,]/Y.[3,],Y.[2,]/Y.[3,],Y[3,]/Y[3,])
lm.out <- lm(t(Y)~t(X)-1)
Y.. <- t(lm.out$coeff)  %*% X
points(Y..[1,]/Y..[3,],Y..[2,]/Y..[3,],col=2,type="l")

RANSAC (Random Sampling Consensus)
- n次元の射影をn+1次元の同次座標で考えるとする
- 変換前後のn次元座標が多数の点ペアについて得られているときに、変換行列を推定することにする
- 必要なのは(n+1)x(n+1)行列を推定したいということだが、この行列の定数倍は同じものであるので、推定自由度は(n+1)^2-1
- １つの変換前後のペアについて、n+1座標の等式ができるが、変換後の座標はn+1個の値(同次座標)からn個の値に直すので、実際に座標の対応関係は、１ペアあたりn個の等式を与える
- nx(n+2) = (n+1)^2-1 であるから、n+2個の点ペアについての情報を集めれば、行列は推定できる
- もし、n+2個の点ペアが、「完璧」な座標として得られていれば、変換行列は確定的に決まる
- 乱雑項がはいっているときには、決まらないので、うまく推定しないといけない
- どうやるか、というと、実は、結構面倒なので、その方法としてRANSACがある
- これは、変換前後の点ペアから、n+2ペアをランダムに取り出し、そこから確定的に行列を計算し、その行列が正しいとみなして、変換をしてやると、実際のデータとどれくらい違うかを調べることができる
- ランダムにn+2ペアでの当てはまりの良さを調べ、一番良いものを選ぶ
- 当てはまりの尺度にもいろいろあるが、必要に応じて選べばよい

# RANSAC (Random Sampling Consensus)

# 3x3行列の場合の確定的行列算出の確認
my.projection.RNASAC.0 <- function(x,y){
	A <- matrix(c(-y[1,1],-y[1,2],-1,0,0,0,y[1,1]*x[1,1],y[1,2]*x[1,1],x[1,1],
				0,0,0,-y[1,1],-y[1,2],-1,y[1,1]*x[1,2],y[1,2]*x[1,2],x[1,2],
				-y[2,1],-y[2,2],-1,0,0,0,y[2,1]*x[2,1],y[2,2]*x[2,1],x[2,1],
				0,0,0,-y[2,1],-y[2,2],-1,y[2,1]*x[2,2],y[2,2]*x[2,2],x[2,2],
				-y[3,1],-y[3,2],-1,0,0,0,y[3,1]*x[3,1],y[3,2]*x[3,1],x[3,1],
				0,0,0,-y[3,1],-y[3,2],-1,y[3,1]*x[3,2],y[3,2]*x[3,2],x[3,2],
				-y[4,1],-y[4,2],-1,0,0,0,y[4,1]*x[4,1],y[4,2]*x[4,1],x[4,1],
				0,0,0,-y[4,1],-y[4,2],-1,y[4,1]*x[4,2],y[4,2]*x[4,2],x[4,2]),byrow=TRUE,ncol=9)
	B <- A[1:8,1:8]
	h <- solve(B) %*% (- A[,9])
	H <- matrix(c(h,1),byrow=TRUE,3,3)
	tmp <- H %*% t(cbind(y,rep(1,4)))
	print((t(tmp)/tmp[3,])[,1:2])
	
}
x <- matrix(sample(1:100,8),ncol=2)
y <- matrix(sample(1:100,8),ncol=2)
my.projection.RNASAC.0(x,y)

# Xはn.pt x d 行列(同次座標ではなく、実際の座標)
# Yはn.pt x (d+1) 行列
my.projection.RNASAC <- function(X,Y,n.iter=1000){
	n <- length(X[,1])
	d <- length(X[1,])
	D <- (d+2)
	H.hx <- X.hx.2 <- list()
	Y.hx <- X.hx <- list()
	Y.log.hx <- list()
	fit.hx <- rep(0,n.iter)
	s.hx <- matrix(0,n.iter,D)
	for(i in 1:n.iter){
		s <- sample(1:n,D,replace=FALSE)
		s.hx[i,] <- s
		tmp.X <- X[s,]
		tmp.Y <- Y[s,]
		A <- matrix(0,D*d,(d+1)^2)
		for(j in 1:D){
			for(k in 1:d){
				A[(j-1)*d+k,((k-1)*(d+1)+1):((k-1)*(d+1)+(d+1))] <- - tmp.Y[j,]
				A[(j-1)*d+k,(d*(d+1)+1):(d+1)^2] <- tmp.Y[j,] * tmp.X[j,k]
			}
		}
		H <- solve(A[1:(D*d),1:(D*d)]) %*% (- A[,(d+1)^2])
		H.hx[[i]] <- c(H,1)
		X.hx[[i]] <- matrix(H.hx[[i]],byrow=TRUE,d+1,d+1) %*% t(Y)
		tmp <- (t(X.hx[[i]]) / t(X.hx[[i]])[,d+1])[,1:d]
		X.hx.2[[i]] <- tmp
		# 実座標と推定座標との距離の二乗の和をフィッティングにしている
		fit.hx[i] <- sum((X-tmp)^2)
		H.inv <- solve(matrix(H.hx[[i]],byrow=TRUE,d+1,d+1))
		Y.hx[[i]] <- H.inv %*% t(cbind(X,rep(1,n)))
	}
	return(list(H.hx,Y.hx,X.hx,X.hx.2,s.hx,fit.hx))
}

my.X <- t(Z[1:2,])
my.Y <- t(X)
X.ori <- my.X
Y.ori <- my.Y
dim(my.X)
dim(my.Y)
n.iter <- 300
RNASAC.out <- my.projection.RNASAC(my.X,my.Y,n.iter=n.iter)

best <- which(RNASAC.out[[6]]==min(RNASAC.out[[6]]))

par(ask=TRUE)
plot(my.X)
for(i in 1:10){
	plot(my.X)
	points((RNASAC.out[[4]][[i]]),col=2)
}
par(ask=FALSE)

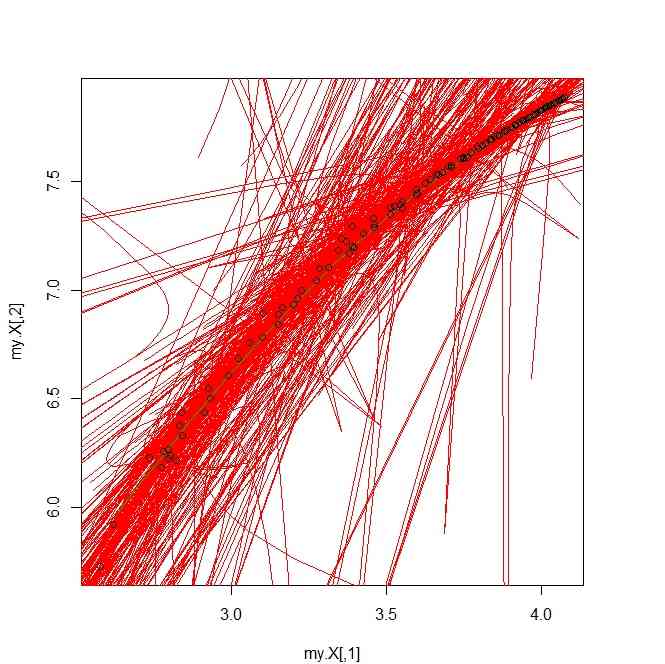
plot(my.X)
for(i in 1:n.iter){
	points((RNASAC.out[[4]][[i]]),col=2,type="l")
}
points((RNASAC.out[[4]][[best]]),col=3,type="l")
points(my.X)