遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

京都大学学部入試数学問題2015で学ぶR

数学 高校数学 R
  • 昨日は国立大学(前期)入学試験の初日。京都大学でも国語と数学の試験がありました。
  • こちらに数学の試験問題(と解答)があります
  • 解説はお任せするとして、Rの練習課題として扱ってみましょう
  • （１）二次元平面に２つの曲線を定め、それをx軸を中心に回転して３次元立体にして体積を考えます。３次元プロットの練習として使います

# ２次元平面関数を作る
# 該当x範囲に等間隔の数列を作る
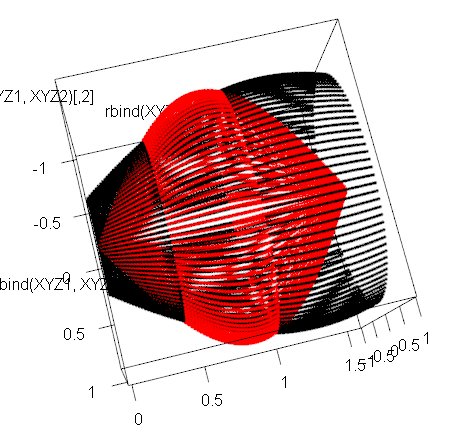
x <- seq(from=0,to=pi/2,length=101)
# 二つの関数のy値と出す。これは、x軸回りの回転の半径に相当する
y1 <- sin(x+pi/8)
y2 <- sin(2*x)
# プロットしてみる
matplot(x,cbind(y1,y2),type="l")
# ３次元にするにあたり、y1,y2を半径として、yz平面の円をx軸に沿って並べる
# x軸回りの円をつくるための角を表す0から2piの等間隔数列
t <- seq(from=0,to=2*pi, length=101)
# y,z単位円座標を2列の行列で作る
YZ <- cbind(cos(t),sin(t))
# 3次元プロット用のパッケージの読み込み
library(rgl)
# 二つの函数のそれぞれに対応する3次元座標の格納用行列を0行3列で作る
XYZ1 <- XYZ2 <- matrix(0,0,3)
# xの値ごとに、yz座標を作成し、それを連結する
for(i in 1:length(x)){
	XYZ1 <- rbind(XYZ1,cbind(rep(x[i],length(t)),y1[i]*YZ))
	XYZ2 <- rbind(XYZ2,cbind(rep(x[i],length(t)),y2[i]*YZ))
}
# 3次元プロット
plot3d(rbind(XYZ1,XYZ2),col=rep(1:2,each=length(XYZ1[,1])))
  • ２）単位円に四角形を外接させます。四角形の２つの角の大きさが決まっているので、決まった角の配置に関する場合分けと、角度が自由な２角は自由度が１なので、それをパラメタにするということにします。２通りある配置のうち、１通りについて、自由度１の分のパラメタを乱数で与えて、描図してみます

# 単位円のx,y座標
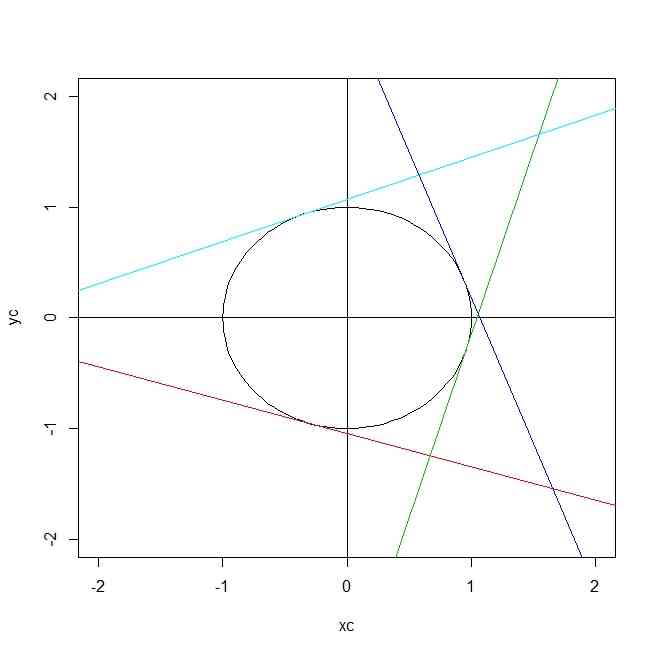
t <- seq(from=0,to=2*pi,length=101)
xc <- cos(t)
yc <- sin(t)
# 内接円の接点極座標を決める
# 接点に対応する角度は、最初の角phi1から、90度、90度＋アルファ、180度＋アルファである
phi1 <- runif(1)*2*pi
phi2 <- runif(1)*pi
thetas <- c(0,pi/2,pi/2+phi2,pi+phi2)+phi1
# 円を描く
plot(xc,yc,type="l",xlim=c(-2,2),ylim=c(-2,2))
# x,y軸線を引く
abline(h=0)
abline(v=0)
# ４接点における接線を引く
for(i in 1:length(thetas)){
	abline(1/sin(thetas[i]),-cos(thetas[i])/sin(thetas[i]),col=i+1)
}
  • （３）指数関数に射影幾何っぽい漸化処理をします。問題設定どおりに、だんだん大きくする計算は、面倒なので、逆からスタートして計算を簡単にすれば、お絵かきは楽です
    • y(x) = e^{x}+1、\frac{d y(x)}{dx} = e^{x}なので、曲線上の点(a,e^a+1)を通る接線はy-e^a+1 = e^a(x-a)であるので、その直線がx軸をよぎる座標は計算できる

# 漸化処理ステップ数
n <- 5
# a1,a2,...,anの座標を格納するベクトル
as <- rep(0,n)
# n番目の値を適当に与える
as[n] <- log(100)
# n-1,n-2,...,1の座標を計算する
for(i in (n-1):1){
	as[i] <- as[i+1]-1-1/exp(as[i+1])
}
# asに対応する曲線上の点のy座標
bs <- exp(as)+1
# 曲線を引くために等間隔x座標を作る
x <- seq(from=-min(as)-1,to=max(as)+1,length=101)
# 対応するy座標を計算する
y <- exp(x)+1
# プロットする
plot(x,y,type="l")
# n個の点をプロットする
points(as,bs,pch=20,col=2)
# 漸近線を引く
abline(h=1)
# 接線を引く
for(i in 1:length(as)){
	p <- exp(as[i])
	q <- exp(as[i])*(-as[i]+1)+1
	abline(q,p,col=3)
}
# 絵を描くのとは別に、a値の間隔が1になる様子を見る
# aの値の幅が1に収束する様子も
n <- 100
as <- bs <-rep(0,n)
as[n] <- 100
for(i in (n-1):1){
	as[i] <- as[i+1]-1-1/exp(as[i+1])
}
as

> as
  [1]   0.7728601   1.9195352   2.9707976   3.9893101   4.9960745   5.9985569
  [7]   6.9994692   7.9998048   8.9999282   9.9999736  10.9999903  11.9999964
 [13]  12.9999987  13.9999995  14.9999998  15.9999999  17.0000000  18.0000000
 [19]  19.0000000  20.0000000  21.0000000  22.0000000  23.0000000  24.0000000
 [25]  25.0000000  26.0000000  27.0000000  28.0000000  29.0000000  30.0000000
 [31]  31.0000000  32.0000000  33.0000000  34.0000000  35.0000000  36.0000000
 [37]  37.0000000  38.0000000  39.0000000  40.0000000  41.0000000  42.0000000
 [43]  43.0000000  44.0000000  45.0000000  46.0000000  47.0000000  48.0000000
 [49]  49.0000000  50.0000000  51.0000000  52.0000000  53.0000000  54.0000000
 [55]  55.0000000  56.0000000  57.0000000  58.0000000  59.0000000  60.0000000
 [61]  61.0000000  62.0000000  63.0000000  64.0000000  65.0000000  66.0000000
 [67]  67.0000000  68.0000000  69.0000000  70.0000000  71.0000000  72.0000000
 [73]  73.0000000  74.0000000  75.0000000  76.0000000  77.0000000  78.0000000
 [79]  79.0000000  80.0000000  81.0000000  82.0000000  83.0000000  84.0000000
 [85]  85.0000000  86.0000000  87.0000000  88.0000000  89.0000000  90.0000000
 [91]  91.0000000  92.0000000  93.0000000  94.0000000  95.0000000  96.0000000
 [97]  97.0000000  98.0000000  99.0000000 100.0000000
  • （４）正四面体を使って、１パラメタで表される指標の最大値の問題。思い切って４次元で考えれば、正単体は簡単。角度を考えるときにスケールはなんでもよいから、そんなことを使えば、R的には簡単です

# ４次元空間の単位ベクトルの先端は正四面体の４頂点に相当する
# 4x4単位行列を作り、それを４点の座標とする
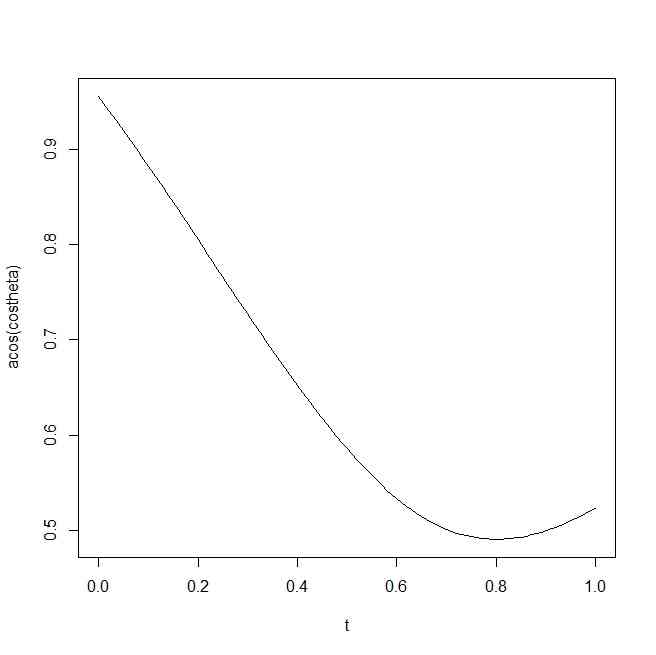
ABCD <- diag(rep(1,4))
A <- ABCD[1,]
B <- ABCD[2,]
C <- ABCD[3,]
D <- ABCD[4,]
# あとは、４次元ベクトル操作だけ
# 中点
P <- (A+B)/2
# 辺上の点を[0,1]範囲のパラメタ表現とする
t <- seq(from=0,to=1,length=101)
Qs <- matrix(0,length(t),4)
for(i in 1:length(t)){
	Qs[i,] <- t[i] * A + (1-t[i])*C
}
# 角度が問題なので、角を作る２ベクトルを単位ベクトル化して内積をとる
DtoP <- P-D
DtoP. <- DtoP/sqrt(sum(DtoP^2))
DtoQs <- t(t(Qs)-D)
DtoQs. <- DtoQs/sqrt(apply(DtoQs^2,1,sum))

costheta <- DtoQs. %*% DtoP.

plot(t,acos(costheta),type="l")
  • （５）多項式環？　証明は河合塾さんにお任せするとして、整数指定すると、整数が出てくることをR的にいじってみる
n <- 1:100

# f(x) = g(x) * (px+q)とする (p,qを整数とする)
d <- rnorm(1)
e <- rnorm(1)
p <- sample((-10:10),1)
q <- sample((-10:10),1)
a <- d*p
b <- d*q + e*p
c <- e*q

F <- a*n^2+b*n+c
G <- d*n+e
H <- F/G
H

> H
  [1]   -5  -10  -15  -20  -25  -30  -35  -40  -45  -50  -55  -60  -65  -70
 [15]  -75  -80  -85  -90  -95 -100 -105 -110 -115 -120 -125 -130 -135 -140
 [29] -145 -150 -155 -160 -165 -170 -175 -180 -185 -190 -195 -200 -205 -210
 [43] -215 -220 -225 -230 -235 -240 -245 -250 -255 -260 -265 -270 -275 -280
 [57] -285 -290 -295 -300 -305 -310 -315 -320 -325 -330 -335 -340 -345 -350
 [71] -355 -360 -365 -370 -375 -380 -385 -390 -395 -400 -405 -410 -415 -420
 [85] -425 -430 -435 -440 -445 -450 -455 -460 -465 -470 -475 -480 -485 -490
 [99] -495 -500
  • （６）確率過程、がたぼこ酔歩。Rは酔歩は得意

# 試行回数
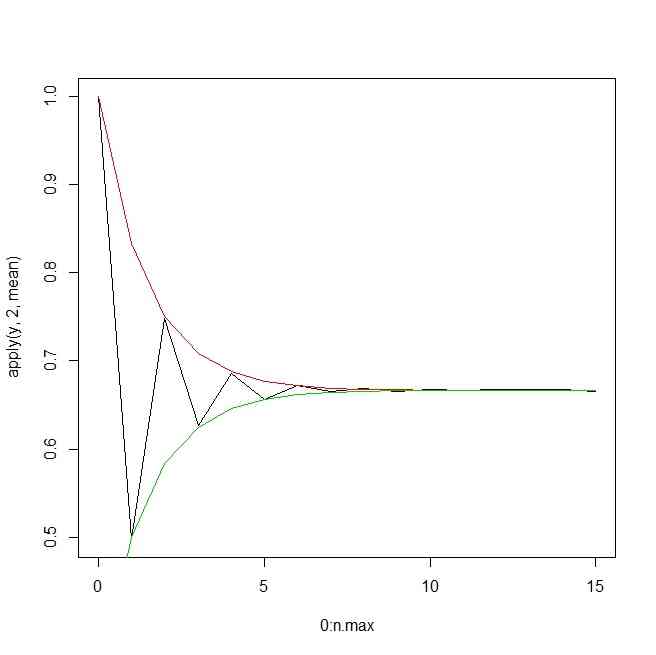
n.iter <- 10^5
# 最大歩数
n.max <- 15
x <- matrix(0,n.iter,n.max+1)
x[,1] <- 1/2 # スタート位置はいつも同じ
r <- matrix(runif(n.iter*n.max),ncol=n.max)
for(i in 1:n.iter){
	for(j in 1:n.max){
		if(r[i,j] < 0.5){
			x[i,j+1] <- x[i,j]/2
		}else{
			x[i,j+1] <- (x[i,j]+1)/2
		}
	}
}
# 条件の合致
y <- x < 2/3
# 合致した点の割合は列平均の計算でわかる
av <- apply(y,2,mean)
plot(0:n.max,av,type="l")
# 理論線を追加する
points(0:n.max,(1/2)^(0:n.max)*1/3+2/3,type="l",col=2)
points(0:n.max,-(1/2)^(0:n.max)*1/3+2/3,type="l",col=3)