- 無限空間酔歩
-
- 格子酔歩
- p=1,2,...任意次元の格子の酔歩は基本
- 正規乱数酔歩
- 一歩の方向を連続値とし、歩幅も連続量とする酔歩も基本
- 中心を持つ酔歩
- 無限空間酔歩は、平均位置こそ原点だが、位置の分散はどんどん大きくなる
- 中心を持つ酔歩では、ある点に束縛された酔歩
- 有限空間の酔歩
- 正の値に限局する・ディリクレ正単体内に限局する・球面に限局する、など、複数要素のベクトルが限局空間内で酔歩することもある
- そのような酔歩シミュレーションでは、ランダムに次の位置を発生させつつ、採択してはいけない点、採択にあたって、確率的に採択するなどの制約が入る
- 以下では、多次元球内、多次元球面、任意次元正単体の酔歩を実行する
- 滑らかな酔歩
- 酔歩を離散シミュレーションするとガタボコする
- 酔歩がいたるところ微分不可能であることとも関係することである
- ただし、現実世界(生物現象界)でのランダムな変化は、結構なめらかである
- これは、変数の変化量が他の変数の関数となっており、いろいろなところで離散的な酔歩変化があるのだが、個々の変数の値の変化の場合はその値の変化そのものが酔歩変化するのではなくて、時間微分が酔歩変化(ガタボコ変化だが変化ベクトルは連続)であること(のようなこと)による
- したがって、速度ベクトルに酔歩をおこし、その結果として変数の値の変化をシミュレーションし、結果として滑らかな酔歩をさせてみる
- 無制限空間・有限空間のそれぞれで実施する
- Rmdファイルは以下(これをhtml化、epub化する方法はこちら)
- epubはこちらからも。

---
title: "randomWafk"
author: "ryamada"
date: "Sunday, February 08, 2015"
output: html_document
---
```{r,echo=FALSE}
library(knitr)
library(rgl)
library(MCMCpack)
```
まずは普通に1次元格子上の酔歩
```{r}
p <- 1
n.step <- 10^4
x <- sample(c(-1,1),n.step,replace=TRUE)
x[1] <- 0
x <- cumsum(x)
plot(x,type="l")
```
二次元格子上の酔歩を2種類
```{r}
p <- 2
n.step <- 10^4
x <- matrix(sample(c(-1,1),n.step*p,replace=TRUE),ncol=p)
x[1,] <- 0
x <- apply(x,2,cumsum)
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
```{r}
p <- 2
n.step <- 10^4
x <- matrix(sample(c(-1,1),n.step*p,replace=TRUE),ncol=p)
s <- sample(1:p,n.step,replace=TRUE)
x. <- matrix(0,n.step,p)
for(i in 1:p){
a <- which(s==i)
x.[a,i] <- x[a,i]
}
x. <- apply(x.,2,cumsum)
par(mfcol=c(1,2))
plot(x.,type="l",asp=1)
matplot(x.,type="l")
par(mfcol=c(1,1))
```
方向を連続変化にして酔歩。ただし1歩の歩幅は定幅
```{r}
p <- 2
n.step <- 10^4
x <- matrix(rnorm(n.step*p),ncol=p)
x <- x/sqrt(apply(x^2,1,sum))
x[1,] <- 0
x <- apply(x,2,cumsum)
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
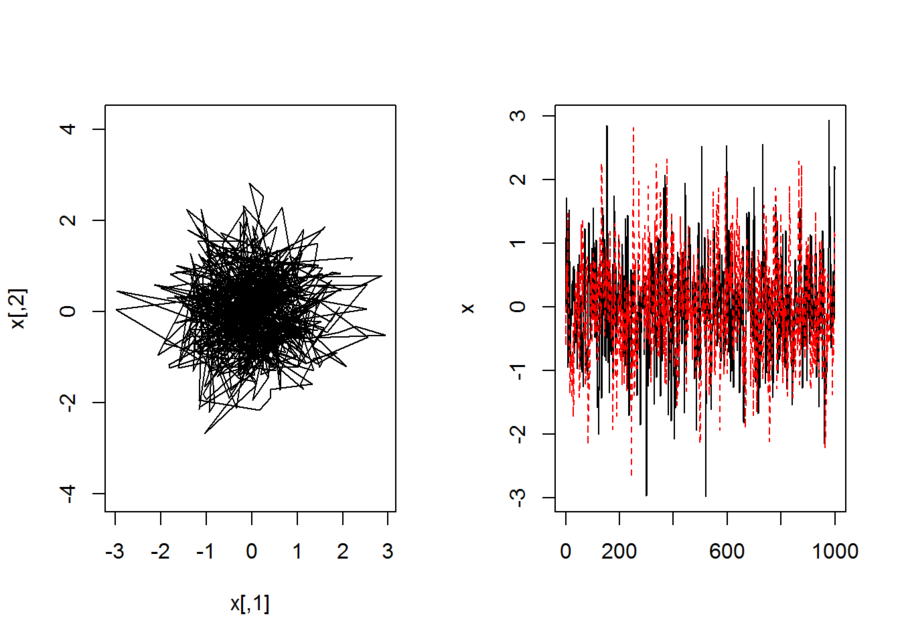
1歩をp次元正規乱点ベクトルとする酔歩
```{r}
p <- 2
n.step <- 10^4
x <- matrix(rnorm(n.step*p),ncol=p)
#x <- x/sqrt(apply(x^2,1,sum))
x[1,] <- 0
x <- apply(x,2,cumsum)
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
これまでの酔歩は、平均位置は原点であるが、存在位置の分散はどんどん大きくなるような酔歩。
中心から遠ざかるに連れて、さらに遠ざかる一歩より、中心に向かう一歩の方が多くなるようにして、無限遠では、必ずさらに遠くなる一歩を踏み出す確率が0になるようにする
なんらかの制御機構があって、ある点の周辺にとどまりつつランダムに位置を変えることは、比較的頻繁に目にする。
```{r}
p <- 2
n.step <- 10^3
v <- matrix(rnorm(n.step*p),ncol=p)
L.step <- abs(rnorm(n.step))
x <- matrix(0,n.step,p)
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
p-正単体内に限定した酔歩を考える。
辺縁に近づくと、それより辺縁方向に進むよりも中心に戻るような一歩を踏み出す確率が高くなるような酔歩では、そのようになる。
辺縁にぶつかって、反射するような酔歩でもそのようになるが、今回は、辺縁に近づくと、戻ってくる方向への一歩を取りやすくするものとする。
$\frac{dx}{dt} = x\times f(y)$というような微分方程式が成り立っているとき、$x=0$付近での変化量は0となり、それ以外の変数(y)の変化だけがあるような状況となるが、そのような場合に相当する。
制限空間内に乱点を発生させ、その中から1点を選び、その方向へと進めることで、辺縁が近い方向への一歩は発生しにくくなる。
辺縁までの距離に比例して少なくするには、制限空間内に一様乱数を発生させればよい。
```{r}
# 正単体座標を計算する関数
CategoryVector<-
function (nc = 3)
{
df <- nc - 1
d <- df + 1
diagval <- 1:d
diagval <- sqrt((df + 1)/df) * sqrt((df - diagval + 1)/(df -
diagval + 2))
others <- -diagval/(df - (0:(d - 1)))
m <- matrix(rep(others, df + 1), nrow = df + 1, byrow = TRUE)
diag(m) <- diagval
m[upper.tri(m)] <- 0
as.matrix(m[, 1:df])
}
```
```{r}
p <- 2
n.step <- 10^3
# 正単体内の一様乱点はディリクレ分布
v <- rdirichlet(n.step,rep(1,p)) # 制限空間内一様乱数
L.step <- abs(rnorm(n.step))*10^(-2)
x <- matrix(0,n.step,p)
x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
3次元の場合
```{r}
p <- 3
n.step <- 10^4
cv <- CategoryVector(p)
v <- rdirichlet(n.step,rep(1,p))
L.step <- abs(rnorm(n.step))*10^(-2)
x <- matrix(0,n.step,p)
x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
```
```{r}
par(mfcol=c(1,2))
plot(x %*% cv,type="l",asp=1,xlim=range(cv[,1]),ylim=range(cv[,2]))
points(cv[c(1,2,2,3,3,1),],type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```
```{r setup}
knit_hooks$set(rgl = hook_rgl)
```
```{r,rgl=TRUE}
plot3d(x,type="l",asp=1,axes=FALSE)
segments3d(rbind(c(1,0,0),c(0,1,0),c(1,0,0),c(0,0,1),c(0,1,0),c(0,0,1)),col=2)
```
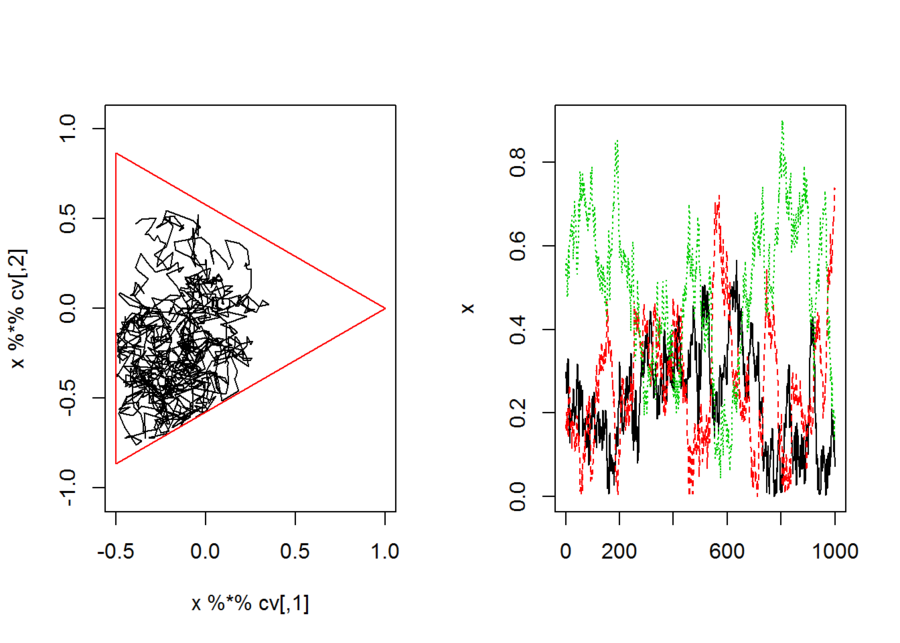
中心を変えてみる。正単体の中心は、酔歩乱数を発生させるディリクレ乱数のパラメタで指定できる。このようにすると、中心に戻りやすく、辺縁には進みにくい一歩がランダム生成できる。
```{r}
p <- 3
n.step <- 10^4
cv <- CategoryVector(p)
# 中心を変えてみる
v <- rdirichlet(n.step,c(0.01,0.01,0.001))
L.step <- abs(rnorm(n.step))*10^(-2)
x <- matrix(0,n.step,p)
x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
```
```{r}
par(mfcol=c(1,2))
plot(x %*% cv,type="l",asp=1,xlim=range(cv[,1]),ylim=range(cv[,2]))
points(cv[c(1,2,2,3,3,1),],type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```
```{r,rgl=TRUE}
plot3d(x,type="l",asp=1,axes=FALSE)
segments3d(rbind(c(1,0,0),c(0,1,0),c(1,0,0),c(0,0,1),c(0,1,0),c(0,0,1)),col=2)
```
上の正単体の例では、正単体内の乱点分布(ディリクレ乱点)を利用して正単体内酔歩をさせた。
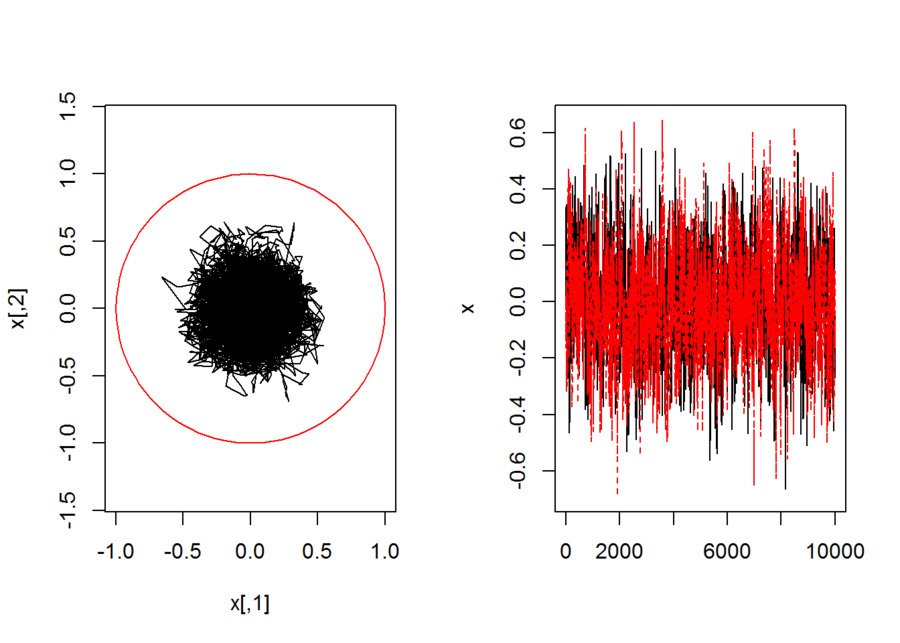
球の場合は球内乱点を使えばよい。
球内一様分布を使ってみる。
球内一様乱数は、球面一様乱数を発生させ(多次元正規乱数の方向平等性を用いる)、その上で、半径ごとの球表面積比に応じて半径を定める。
```{r}
runif.sphere <- function(n,p){
Rcp <- matrix(rnorm(n*p),ncol=p)
d <- sqrt(apply(Rcp^2,1,sum))
Rcp. <- Rcp/d
q <- runif(n) # uniform random values as quantile values
Q <- q^(1/(p)) # Inverse function of cdf
Rcp.. <- Rcp. * Q
Rcp..
}
r <- runif.sphere(n.step,p)
plot3d(r)
```
```{r}
p <- 2
n.step <- 10^4
v <- runif.sphere(n.step,p)
L.step <- abs(rnorm(n.step))*10^(-1)
x <- matrix(0,n.step,p)
x[1,] <- rep(0,p)
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
par(mfcol=c(1,2))
plot(x, type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1))
t <- seq(from=0,to=1,length=100)*2*pi
X <- cos(t);Y <- sin(t)
points(X,Y,type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```
```{r}
p <- 3
n.step <- 10^4
v <- runif.sphere(n.step,p)
L.step <- abs(rnorm(n.step))*10^(-1)
x <- matrix(0,n.step,p)
x[1,] <- rep(0,p)
for(i in 2:n.step){
u <- v[i,] - x[i-1,]
u. <- L.step[i] * u/sqrt(sum(u^2))
x[i,] <- x[i-1,] + u.
}
matplot(x,type="l")
```
```{r,rgl=TRUE}
XYZ <- matrix(rnorm(n.step*p),ncol=p)
XYZ <- XYZ/sqrt(apply(XYZ^2,1,sum))
plot3d(XYZ,size=0.1,col=2)
tmp <- rep(1:n.step,each=2)
tmp <- tmp[c(-1,-n.step*2)]
segments3d(x[tmp,])
```
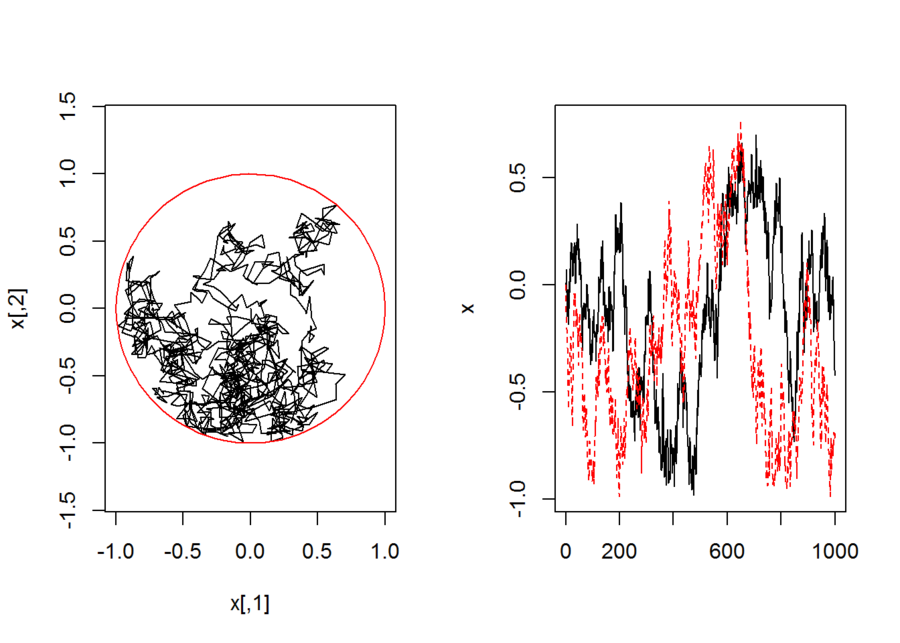
上記では、制限範囲内に中心を持つ酔歩であった。
制限範囲内であれば、一様に動き回らせることにする。
有限範囲内に乱点を発生させ、近傍乱点へと移動することで、有限範囲内酔歩をさせる。
逆に言えば、乱点を発生させ、範囲内であれば、定確率で、範囲外であれば、確率0で採択するような酔歩である。
円の場合
```{r}
p <- 2
n.step <- 10^3
n.neighbor <- 10^2 # 酔歩の粗さを決めるパラメタ
x <- matrix(0,n.step,p)
x[1,] <- rep(0,p)
for(i in 2:n.step){
tmp <- runif.sphere(n.neighbor,p)
tmp. <- t(t(tmp)-x[i-1,])
d <- apply(tmp.^2,1,sum)
nn <- which(d==min(d))
x[i,] <- tmp[nn,]
}
par(mfcol=c(1,2))
plot(x, type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1))
t <- seq(from=0,to=1,length=100)*2*pi
X <- cos(t);Y <- sin(t)
points(X,Y,type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```
球の場合
```{r}
p <- 3
n.step <- 10^3
n.neighbor <- 10^2 # 酔歩の粗さを決めるパラメタ
x <- matrix(0,n.step,p)
x[1,] <- rep(0,p)
for(i in 2:n.step){
tmp <- runif.sphere(n.neighbor,p)
tmp. <- t(t(tmp)-x[i-1,])
d <- apply(tmp.^2,1,sum)
nn <- which(d==min(d))
x[i,] <- tmp[nn,]
}
matplot(x,type="l")
```
```{r,rgl=TRUE}
XYZ <- matrix(rnorm(n.step*p),ncol=p)
XYZ <- XYZ/sqrt(apply(XYZ^2,1,sum))
plot3d(XYZ,size=0.1,col=2)
tmp <- rep(1:n.step,each=2)
tmp <- tmp[c(-1,-n.step*2)]
segments3d(x[tmp,])
```
球面の場合は、少し違う。
球面の場合は、存在位置から、指定角だけ、適当な方向に進ませる。
下のコードでは、存在位置の周囲に球面一様乱点を発生させ、それを、進行方向一様乱点とし、指定角相当の座標を計算している。
```{r}
angular.move <- function(x,y,theta){
x. <- x/sqrt(sum(x^2))
y. <- y/sqrt(sum(y^2))
ctheta <- (sum(x. * y.))
# 方向ベクトルのうち位置ベクトルと垂直な成分
tmp <- y. - x.*ctheta
# 垂直ベクトルを単位ベクトル化
tmp <- tmp/sqrt(sum(tmp^2))
# 一歩の角から、一歩先の単位球面点を通るベクトルを位置ベクトルと方向ベクトルの線形和に表すための係数を算出
# 移動空間である単位球と、位置ベクトルを中心とする単位球とに関して、位置ベクトルと、方向ベクトルとが作る2次元平面を切り出して、そこで2次元幾何計算をする
Q <- tan(2*theta)
a <- 1/(Q+1)
b <- Q/(Q+1)
# 位置ベクトルと方向単位ベクトルとの線形和
z <- a*x. + b*tmp
# それを位置ベクトルを中心とする単位球面上に伸ばす
z <- z/sqrt(sum(z^2))
# 移動先の点と移動空間中心とを結ぶ直線上の点
ret <- x + z
# それを移動空間上に射影
ret/sqrt(sum(ret^2))*sqrt(sum(x^2))
}
sphere.brownian <- function(n.step,p=3,x.init=c(1,rep(0,p-1)),phis=rep(0.01,n.step)){
R.sp <- function(n,p){
m <- matrix(rnorm(n*p),ncol=p)
d <- sqrt(apply(m^2,1,sum))
m/d
}
S <- R.sp(n.step,p)
X <- S
for(i in 2:n.step){
X[i,] <- angular.move(X[i-1,],S[i,],phis[i])
}
X
}
x <- sphere.brownian(n.step=10000,p=3,phis=rep(0.1,10000))
```
```{r,rgl=TRUE}
XYZ <- matrix(rnorm(n.step*p*10),ncol=p)
XYZ <- XYZ/sqrt(apply(XYZ^2,1,sum))
plot3d(XYZ,col=5)
tmp <- rep(1:n.step,each=2)
tmp <- tmp[c(-1,-n.step*2)]
segments3d(x[tmp,])
```
```{r}
matplot(X,type="l")
```
正単体の内部の一様酔歩。正単体内に一様乱数を発生させ、最近接乱点へと移動させる。
3次元の例。二次元平面の正三角形内の酔歩として描画できる。
```{r}
p <- 3
n.step <- 10^3
n.neighbor <- 10^2 # 酔歩の粗さを決めるパラメタ
x <- matrix(0,n.step,p)
x[1,] <- x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
tmp <- rdirichlet(n.neighbor,rep(1,p))
tmp. <- t(t(tmp)-x[i-1,])
d <- apply(tmp.^2,1,sum)
nn <- which(d==min(d))
x[i,] <- tmp[nn,]
}
```
```{r}
cv <- CategoryVector(p)
par(mfcol=c(1,2))
plot(x %*% cv,type="l",asp=1,xlim=range(cv[,1]),ylim=range(cv[,2]))
points(cv[c(1,2,2,3,3,1),],type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```
```{r,rgl=TRUE}
plot3d(x,type="l",asp=1,axes=FALSE)
segments3d(rbind(c(1,0,0),c(0,1,0),c(1,0,0),c(0,0,1),c(0,1,0),c(0,0,1)),col=2)
```
3次元空間内の3-正単体(正四面体)の例。
```{r}
p <- 4
n.step <- 10^3
n.neighbor <- 10^2 # 酔歩の粗さを決めるパラメタ
x <- matrix(0,n.step,p)
x[1,] <- x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
tmp <- rdirichlet(n.neighbor,rep(1,p))
tmp. <- t(t(tmp)-x[i-1,])
d <- apply(tmp.^2,1,sum)
nn <- which(d==min(d))
x[i,] <- tmp[nn,]
}
```
```{r}
cv <- CategoryVector(p)
plot(x %*% cv,type="l",asp=1,xlim=range(cv[,1]),ylim=range(cv[,2]))
matplot(x,type="l")
```
```{r,rgl=TRUE}
plot3d(x %*% cv,type="l",asp=1,axes=FALSE)
segments3d(cv[c(1,2,1,3,1,4,2,3,2,4,3,4),],col=2)
```
一歩、一歩、方向を変えるとガタボコな軌道になる。
ランダムウォーク的に変わるのが、位置ではなくて、速度であれば、速度変化は微分できないが、連続になるので、位置変化は滑らかになる。
二次元平面の場合。1歩は定幅。
```{r}
p <- 2
n.step <- 10^4
v <- matrix(rnorm(n.step*p),ncol=p)
v <- v/sqrt(apply(v^2,1,sum))
x <- matrix(0,n.step,p)
x[1,] <- 0
r <- 0.1 # 1歩の幅に対して、加速度ベクトルの長さの比率
for(i in 2:n.step){
if(i==2){
x[i,] <- x[i-1,]+v[i,]
}else{
tmp <- v[i-1,]+r*v[i,]
tmp <- tmp/sqrt(sum(tmp^2))
v[i,] <- tmp
x[i,] <- x[i-1,]+v[i,]
}
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
3次元でも同じ。
```{r}
p <- 3
n.step <- 10^4
v <- matrix(rnorm(n.step*p),ncol=p)
v <- v/sqrt(apply(v^2,1,sum))
x <- matrix(0,n.step,p)
x[1,] <- 0
r <- 0.1
for(i in 2:n.step){
if(i==2){
x[i,] <- x[i-1,]+v[i,]
}else{
tmp <- v[i-1,]+r*v[i,]
tmp <- tmp/sqrt(sum(tmp^2))
v[i,] <- tmp
x[i,] <- x[i-1,]+v[i,]
}
}
matplot(x,type="l")
```
```{r,rgl=TRUE}
plot3d(x,type="l")
```
歩幅が不定
```{r}
p <- 2
n.step <- 10^4
v <- matrix(rnorm(n.step*p),ncol=p)
v <- v/sqrt(apply(v^2,1,sum))
L.step <- abs(rnorm(n.step)) # 歩幅を指定
x <- matrix(0,n.step,p)
x[1,] <- 0
r <- 0.1
for(i in 2:n.step){
if(i==2){
x[i,] <- x[i-1,]+v[i,]
}else{
tmp <- v[i-1,]+r*sqrt(sum(v[i-1,]^2))*v[i,]
tmp <- tmp/sqrt(sum(tmp^2))*L.step[i]
v[i,] <- tmp
x[i,] <- x[i-1,]+v[i,]
}
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
現時点の速度を基準に、加速度を正規乱点として発生させ、到達点候補を作成する。
到達点候補をたくさん作ればつくるほど、きめの細かい酔歩となり、また、加速度ベクトルの長さの、速度ベクトルの長さに対する割合を調整することで、曲がりやすさを調節する。
その到達点のうち、中心に向かう点は高確率で、遠ざかる点は低確率で採択する。
下の例では、その採択確率を、原点中心の正規分布としている。
```{r}
p <- 2
n.step <- 10^3
n.neighbor <- 10^2
r <- 0.5
L.step <- rep(0.5,n.step)
x <- matrix(0,n.step,p)
v <- matrix(0,n.step,p)
for(i in 2:n.step){
if(i==2){
tmp.v <- rnorm(p)*L.step[i]
v[i,] <- tmp.v
x[i,] <- x[i-1,] + v[i,]
}else{
tmp.v <- matrix(rnorm(n.neighbor*p),ncol=p)
tmp.v <- tmp.v/sqrt(apply(tmp.v^2,1,sum))
tmp.v <- tmp.v*r
tmp.v2 <- t(t(tmp.v) + v[i-1,])
tmp.v2 <- tmp.v2/sqrt(apply(tmp.v2^2,1,sum))*L.step[i]
tmp <-t(t(tmp.v2)+x[i-1,])
tmp.L <- sqrt(apply(tmp^2,1,sum))
#tmp.pr <- dnorm(tmp.L)
tmp.pr <- exp(-(tmp.L^2-min(tmp.L^2)))
p.vec <- tmp.pr/(sum(tmp.pr))
v.select <- sample(1:n.neighbor,1,prob=p.vec)
v[i,] <- v[i-1,]+tmp.v[v.select,]
x[i,] <- x[i-1,]+v[i,]
}
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
歩幅ばらばらにする。ステップごとに歩幅を決め、その決めた歩幅に関して、乱点発生して、確率的採択をする。
```{r}
p <- 2
n.step <- 10^3
n.neighbor <- 10^2
r <- 0.5
L.step <- abs(rnorm(n.step))
x <- matrix(0,n.step,p)
v <- matrix(0,n.step,p)
for(i in 2:n.step){
if(i==2){
tmp.v <- rnorm(p)*L.step[i]
v[i,] <- tmp.v
x[i,] <- x[i-1,] + v[i,]
}else{
tmp.v <- matrix(rnorm(n.neighbor*p),ncol=p)
tmp.v <- tmp.v/sqrt(apply(tmp.v^2,1,sum))
tmp.v <- tmp.v*r
tmp.v2 <- t(t(tmp.v) + v[i-1,])
tmp.v2 <- tmp.v2/sqrt(apply(tmp.v2^2,1,sum))*L.step[i]
tmp <-t(t(tmp.v2)+x[i-1,])
tmp.L <- sqrt(apply(tmp^2,1,sum))
#tmp.pr <- dnorm(tmp.L)
tmp.pr <- exp(-(tmp.L^2-min(tmp.L^2)))
p.vec <- tmp.pr/(sum(tmp.pr))
v.select <- sample(1:n.neighbor,1,prob=p.vec)
v[i,] <- v[i-1,]+tmp.v[v.select,]
x[i,] <- x[i-1,]+v[i,]
}
}
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
```
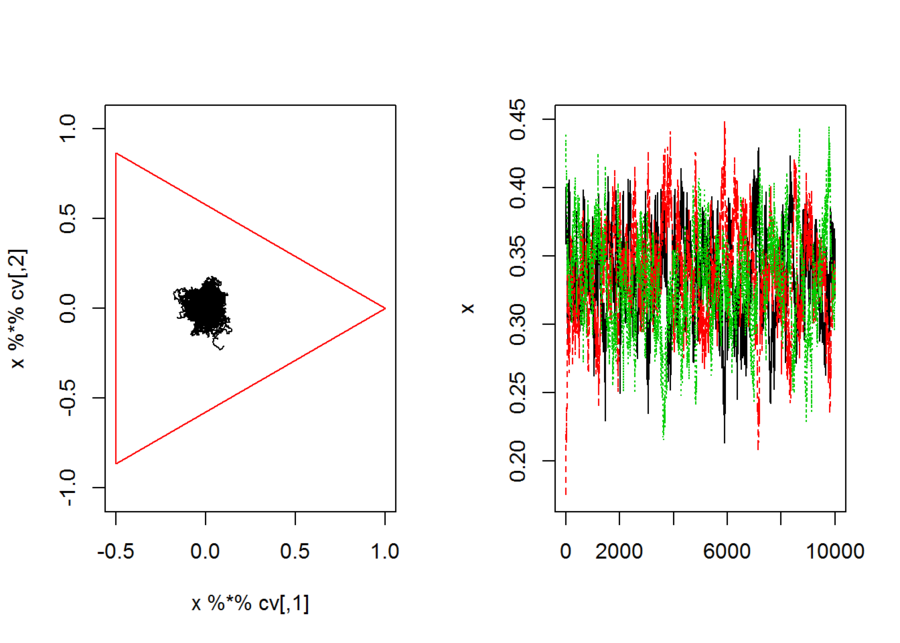
前の例では、確率的採択において、中心からの距離などを採用した。
まんべんなく歩く場合には、制限空間内の点であれば、どの点も等確率で採択する。
```{r}
p <- 3
n.step <- 10^4
n.neighbor <- 10^2
# 正単体内の一様乱点はディリクレ分布
v <- matrix(0,n.step,p) # 制限空間内一様乱数
L.step <- abs(rnorm(n.step))*10^(-2)
r <- 0.1
x <- matrix(0,n.step,p)
x[1,] <- rdirichlet(1,rep(1,p))
for(i in 2:n.step){
tmp.v <- (as.matrix(rdirichlet(n.neighbor,rep(1,p)))- 1/p)
tmp.v <- tmp.v/sqrt(apply(tmp.v^2,1,sum))
tmp.v <- tmp.v*r
tmp.v2 <- t(t(tmp.v) + v[i-1,])
tmp.v2 <- tmp.v2/sqrt(apply(tmp.v2^2,1,sum))*L.step[i]
tmp <-t(t(tmp.v2)+x[i-1,])
tmp2 <- (tmp>=0)
tmp.pr <- apply(tmp2,1,prod)
p.vec <- tmp.pr/(sum(tmp.pr))
v.select <- sample(1:n.neighbor,1,prob=p.vec)
v[i,] <- tmp.v2[v.select,]
x[i,] <- x[i-1,]+v[i,]
}
```
```{r}
cv <- CategoryVector(p)
par(mfcol=c(1,2))
plot(x %*% cv,type="l",asp=1,xlim=range(cv[,1]),ylim=range(cv[,2]))
points(cv[c(1,2,2,3,3,1),],type="l",col=2)
matplot(x,type="l")
par(mfcol=c(1,1))
```

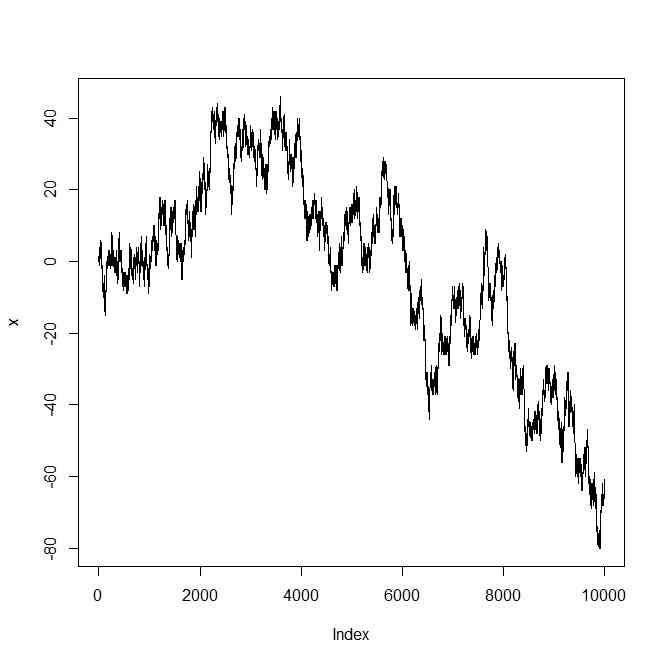
p <- 1
n.step <- 10^4
x <- sample(c(-1,1),n.step,replace=TRUE)
x[1] <- 0
x <- cumsum(x)
plot(x,type="l")
-
- p=2次元、1歩は(1,1),(1,-1),(-1,1),(-1,-1)のいずれか
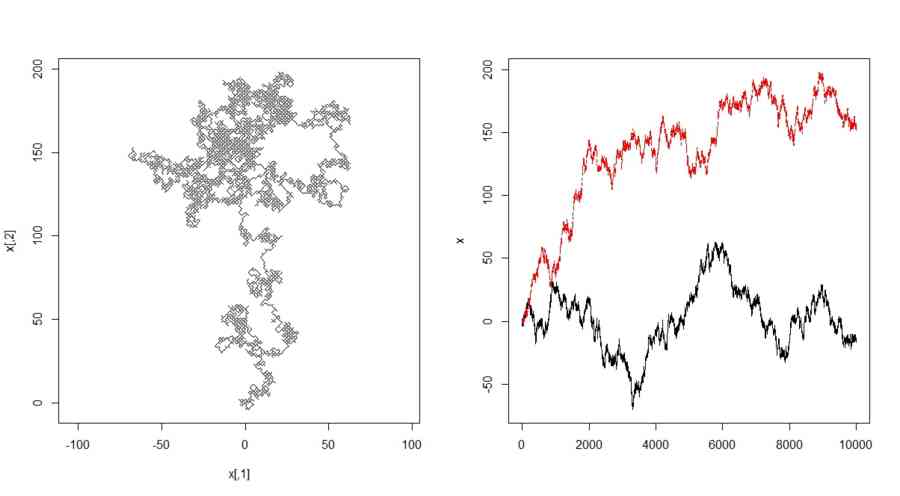
p <- 2
x <- matrix(sample(c(-1,1),n.step*p,replace=TRUE),ncol=p)
x[1,] <- 0
x <- apply(x,2,cumsum)
par(mfcol=c(1,2))
plot(x,type="l",asp=1)
matplot(x,type="l")
par(mfcol=c(1,1))
-
- p=2次元、1歩は(1,0),(-1,0),(0,1),(0,-1)のいずれか
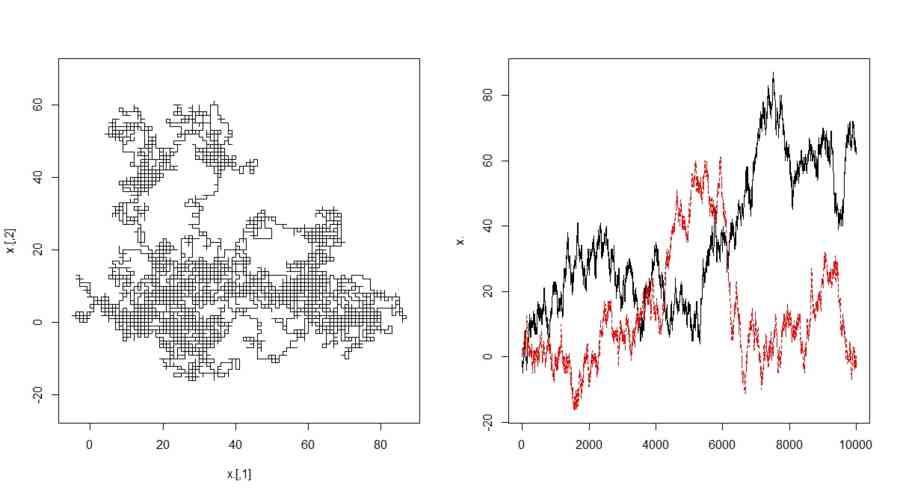
p <- 2
x <- matrix(sample(c(-1,1),n.step*p,replace=TRUE),ncol=p)
s <- sample(1:p,n.step,replace=TRUE)
x. <- matrix(0,n.step,p)
for(i in 1:p){
a <- which(s==i)
x.[a,i] <- x[a,i]
}
x. <- apply(x.,2,cumsum)
par(mfcol=c(1,2))
plot(x.,type="l",asp=1)
matplot(x.,type="l")
par(mfcol=c(1,1))









