1. Supervised learning ぱらぱらめくるscikit-learnのUser guide

• 1.1 Generalized Linear Models
• 1.1.1 普通の線形回帰

from sklearn import linear_model
clf = linear_model.LinearRegression()
x = [[0, 0], [1, 1], [2, 2]]
y = [0, 1, 2]

clf.fit (x, y)
clf.coef_
clf.intercept_

• • xは二次元アレイ、yは一次元アレイ。clfオブジェクトへのfitの実行は、

x
Out[154]: [[0, 0], [1, 1], [2, 2]]
y
Out[155]: [0, 1, 2]
clf.fit(x,y)
Out[156]: LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
clf.coef_
Out[165]: array([ 0.5,  0.5])
clf.intercept_
Out[166]: 1.1102230246251565e-16

• • 切片なしのモデルは次のようにやる
    • clfオブジェクトのデフォルトのfit_intercept設定はTrueなので、それをFalseにしてから回帰する

clf.fit_intercept
clf.fit_intercept = False # clf = linear_model.LinearRegression(fit_intercept=False)でもOK
clf.fit_intercept
clf.fit(x,y)
clf.coef_
clf.intercept_

clf.fit_intercept
Out[158]: True
clf.fit_intercept
Out[160]: False
clf.fit(x,y)
Out[161]: LinearRegression(copy_X=True, fit_intercept=False, n_jobs=1, normalize=False)
clf.coef_
Out[162]: array([ 0.5,  0.5])
clf.intercept_
Out[166]: 0.0

• • 乱数を用いて、線形モデルを作成して回帰する

import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下２つを入れる
import matplotlib as mp 
import pylab as pl
import os # コンピュータのファイルの出し入れのため

n = 100
d = 1
x = np.array(sp.randn(n*d))
# xは二次元
x.shape = (n,d)
x
a1 = 3.4
a2 = 2.3

err = sp.randn(n) * 0.5
# y は１次元
y = a1 * x[:,0] + a2 + err
plot(x,y,"o")

clf.fit(x,y)
clf.coef_
clf.intercept_

x2 = np.array([x[:,0],np.ones(n)]).T

y = a1 * x2[:,0] + a2 * x2[:,1] + sp.randn(n)*0.1

clf.fit(x2,y,intercept=FALSE)
clf.coef_

clf.fit(x[:,0],y)

pl.plot(x[:,0],y,"o")

import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下２つを入れる
import matplotlib as mp 
import pylab as pl
import os # コンピュータのファイルの出し入れのため


from sklearn import linear_model
n = 100
d = 5
x = np.array(sp.randn(n*d))
x.shape = (n,d)
x
a1 = 3.4
a2 = 2.3

err = sp.randn(n) * 0.5
y = a1 * x[:,0] + a2 * x[:,1] + sp.randn(n)*0.1

clf.fit(x,y)
clf.coef_
clf.intercept_

• • 1.1.2 リッジ回帰
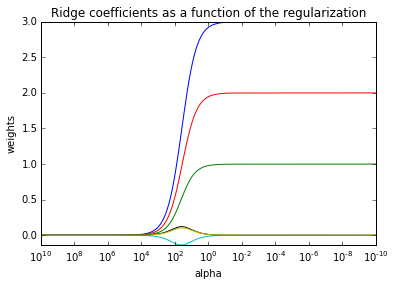
    • 制約付き回帰：係数の二乗和が大きくならないような制約を入れる
    • 制約の強さを１変数でパラメタ化する。パラメタが大きければ、すべての変数の係数が0になり、パラメタが小さければ、線形回帰に一致する

import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下２つを入れる
import matplotlib.pyplot as plt
import pylab as pl
import os # コンピュータのファイルの出し入れのため


from sklearn import linear_model
n = 50 # No. samples
d = 6 # No. variables
x = np.array(sp.randn(n*d))
x.shape = (n,d) # Matrix

beta = np.array([3,2,1,0,0,0]) # True coefficients
err = sp.randn(n) * 0.1 # error
y = sp.dot(x,beta) + err # dot() is product of matrix and vector

clf = linear_model.Ridge (alpha = .1) # ridge parameter =0.1

clf.fit (x, y)
clf.coef_ # good estimates
beta

# Compute paths
# estimate with many parameter values
n_alphas = 200
alphas = np.logspace(-10, 10, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)

coefs = []
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(x, y)
    coefs.append(clf.coef_)

# Display results

ax = plt.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

• • Cross validationにより複数のパラメタ値候補の中から、適切なリッジパラメタを返す。クロス・バリデーションによりもっとも安定した推定結果をもたらすパラメタを選ぶ

clf = linear_model.RidgeCV(alphas=alphas)
clf.fit(x, y)     
clf.alpha_   
Out[247]: 0.013826221737646593

• • 1.1.3 Lasso
    • コード上は"linear_model.Ridge"を"linear_model.Lasso"に変えるだけ
    • クロス・バリデーションなどは、特別にsklearn.linear_modelから読み込むものが必要

import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下２つを入れる
import matplotlib.pyplot as plt
import pylab as pl
import os # コンピュータのファイルの出し入れのため


from sklearn import linear_model
from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
import time

n = 50 # No. samples
d = 6 # No. variables
x = np.array(sp.randn(n*d))
x.shape = (n,d) # Matrix

beta = np.array([3,2,1,0,0,0]) # True coefficients
err = sp.randn(n) * 0.1 # error
y = sp.dot(x,beta) + err # dot() is product of matrix and vector

clf = linear_model.Lasso (alpha = .1) # ridge parameter =0.1

clf.fit (x, y)
clf.coef_ # good estimates
beta

# Compute paths
# estimate with many parameter values
n_alphas = 200
alphas = np.logspace(-10, 10, n_alphas)
clf = linear_model.Lasso(fit_intercept=False)

coefs = []
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(x, y)
    coefs.append(clf.coef_)

# Display results

ax = plt.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])

ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
ax.set_ylim([-1,4])
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
#plt.axis('tight')
plt.show()


clf = linear_model.LassoCV(alphas=alphas)
clf.fit(x, y)     
clf.alpha_  

# Compute paths
print("Computing regularization path using the coordinate descent lasso...")
t1 = time.time()
model = LassoCV(cv=20).fit(x, y)
t_lasso_cv = time.time() - t1

# Display results
m_log_alphas = -np.log10(model.alphas_)

plt.figure()
ymin, ymax = 0,4
plt.plot(m_log_alphas, model.mse_path_, ':')
plt.plot(m_log_alphas, model.mse_path_.mean(axis=-1), 'k',
         label='Average across the folds', linewidth=2)
plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k',
            label='alpha: CV estimate')

plt.legend()

plt.xlabel('-log(alpha)')
plt.ylabel('Mean square error')
plt.title('Mean square error on each fold: coordinate descent '
          '(train time: %.2fs)' % t_lasso_cv)
plt.axis('tight')
plt.ylim(ymin, ymax)

• • 1.1.4 Elastic net
    • Exampleコードでpython コーディングの初歩を学ぶ

# 乱数シードの指定
np.random.seed(42)
# 二つの変数にまとめて付値
n_samples, n_features = 50, 200
# 正規乱数行列をいきなり作る
X = np.random.randn(n_samples, n_features)
coef = 3 * np.random.randn(n_features)
# 番地を生成(0始まりで長さがn_featuresの整数ベクトル)
inds = np.arange(n_features)
# シャッフル
np.random.shuffle(inds)
# 10番目(第9番地)以降を0にする
coef[inds[10:]] = 0
# 行列計算
y = np.dot(X, coef)
# インクリメント
y += 0.01 * np.random.normal((n_samples,))

• • • コードはコピペすれば動く
  • 1.1.5 マルチタスク・ラッソ
    • 複数の説明変数があり、複数の従属変数がある。いくつかの説明変数がそろって複数の従属変数に寄与がある。ただしその寄与係数は違う。そんなとき、個々の従属変数についてラッソをやるのではなく、全従属変数(タスク)に対して揃ってラッソ(選ぶべき説明変数のサブセットをそろえつつ、係数推定する。普通のラッソだと、各従属変数(各タスク)に対して係数がついたりつかなかったりするが、マルチタスク・ラッソだと揃ってつく
    • ソースはコピペで動く
  • 1.1.6 Least Angle Regression (LARs)
    • 結果はラッソに似る。幾何学的解探索

import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下２つを入れる
import matplotlib.pyplot as plt
import pylab as pl
import os # コンピュータのファイルの出し入れのため


from sklearn import linear_model
from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
import time

n = 50 # No. samples
d = 6 # No. variables
x = np.array(sp.randn(n*d))
x.shape = (n,d) # Matrix

beta = np.array([3,2,1,0,0,0]) # True coefficients
err = sp.randn(n) * 0.1 # error
y = sp.dot(x,beta) + err # dot() is product of matrix and vector

clf_lasso = linear_model.Lasso (alpha = .001) # ridge parameter =0.1
clf_lars = linear_model.Lars(n_nonzero_coefs=d)
clf_lasso.fit(x,y)
clf_lars.fit(x,y)

print(clf_lasso.coef_)
print(clf_lars.coef_)

• • 1.1.10 ロジスティック回帰
    • pythonでは統計用のモジュールを使えば、ブラックボックス的にロジスティック回帰を実行できるがscikit-learnでは、最適化問題であることが表面に現れている

from sklearn.linear_model import LogisticRegression
C = 10 # regularization parameter
clf_l1_LR = LogisticRegression(C=C, penalty='l1', tol=0.01)
clf_l1_LR.fit(X, y)

• • 1.1.14 RANSAC 外れ値を無視して回帰

import numpy as np
from matplotlib import pyplot as plt

from sklearn import linear_model, datasets


n_samples = 1000
n_outliers = 100


X, y, coef = datasets.make_regression(n_samples=n_samples, n_features=1,
                                      n_informative=1, noise=10,
                                      coef=True, random_state=0)

# Add outlier data
np.random.seed(0)
#X[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 10 * np.random.normal(size=n_outliers)

# Fit line using all data
model = linear_model.LinearRegression()
model.fit(X, y)

# Robustly fit linear model with RANSAC algorithm
model_ransac = linear_model.RANSACRegressor(linear_model.LinearRegression())
model_ransac.fit(X, y)
inlier_mask = model_ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)

# Predict data of estimated models
line_X = np.arange(-5, 5)
line_y = model.predict(line_X[:, np.newaxis])
line_y_ransac = model_ransac.predict(line_X[:, np.newaxis])

# Compare estimated coefficients
print("Estimated coefficients (true, normal, RANSAC):")
print(coef, model.coef_, model_ransac.estimator_.coef_)

plt.plot(X[inlier_mask], y[inlier_mask], '.g', label='Inliers')
plt.plot(X[outlier_mask], y[outlier_mask], '.r', label='Outliers')
plt.plot(line_X, line_y, '-k', label='Linear regressor')
plt.plot(line_X, line_y_ransac, '-b', label='RANSAC regressor')
plt.legend(loc='lower right')
plt.show()

• 1.2 Linear and Quadratic Discriminant Analysis
  • 1.2.1 LDA と QDA
    • 独立変数が0,1の値を持つベクトルで、説明変数が行列であるときに、それぞれ、LDA,QDAをするためのオブジェクトを作成して、それのメンバー関数fit()でDiscriminationをさせる

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
qda = QuadraticDiscriminantAnalysis(store_covariances=True)

• 1.3 Kernel ridge regression
• 1.4 Support Vector Machines
• 1.5 Stochastic Gradient Descent
• 1.6 Nearest Neighbors
• 1.7 Gaussian Processes
• 1.8 Cross Decomposition
• 1.9 Naive Bayes
• 1.10 Decision Tree
• 1.11 Ensemble Methods
• 1.12 Multiclass and Multilabel Algorithm
• 1.13 Feature Selection
• 1.14 Semi-Supervised
• 1.15 Isotonic Regression
• 1.16 Probability Calibration