多次元のフーリエ変換的分解 - ryamadaのコンピュータ・数学メモ

一昨日、１変数関数のフーリエ変換は、複数の円運動の和に分解することと書いた
多変数関数のフーリエ変換を考えよう
複数の円運動がn+1次元空間で起きていて、それをn次元空間に投影すると考えることができそうだ
まず、２次元から
２次元で同周期の円運動があって
- ２次元のそれぞれの変数の位相がそろっているときは、２次元空間に１次元線分があって、その上に周期運動が生じて、その１次元空間上の周期運動は、２次元円運動の１次元空間への影とみなせる。この場合は３次元での円運動が、投影２次元平面に垂直な円になっている
- ２次元の変数の位相が $\frac{\pi}{2}$ ずれているときは、正円を２次元平面に描いている。この場合は３次元での円運動が投影２次元平面と並行な円になっている
- それ以外の場合は両者の間で、２次元平面に楕円を映す
- そんな、放っておけば楕円の影を作るような運動を足し合わせると、楕円の重畳
- それを２変数ごとにフーリエ変換する
- ここで見たいのは、２変数を併せたうえでの寄与分の大きい成分
- それは、２変数のフーリエ分解した周波数が持つ複素数の絶対値のその和が大きいことなので、その値の大小で眺めるとよい

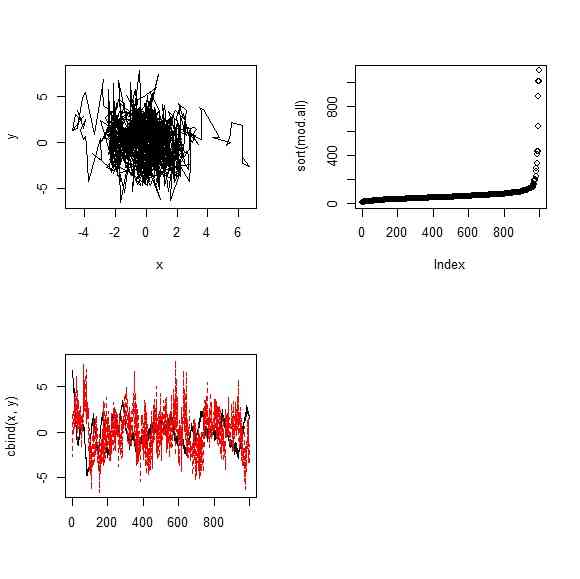
t <- seq(from=0,to=1,length=1000)*2*pi
# 周期と位相とを適当にとって、それぞれに重みをつけて合算する
thetas <- runif(10)*20
deltas <- runif(length(thetas))*2*pi
weights <- runif(length(thetas))
x <- y <- rep(0,length(t))
for(i in 1:length(thetas)){
	x <- x + weights[i] * cos(thetas[i]*t) + rnorm(length(t),0,0.1)
	y <- y + weights[i] * cos(thetas[i]*t + deltas[i]) + rnorm(length(t),0,0.5)
}

plot(x,y,type="l")
matplot(cbind(x,y),type="l")
# フーリエ変換
mv.fft.out <- mvfft(cbind(x,y))
# ２変数のスペクトル絶対値の和で取ると、シミュレーションした周期運動の数の分だけ強い周波数があってそれ以外は乱雑項
mod.all <- apply(Mod(mv.fft.out),1,sum)
plot(sort(mod.all))