2015-01-01

スライシング〜アレイ(ベクトル・行列・アレイ)の扱いを覚える２〜私のためのpythonメモ

python

アレイの要素へのアクセス〜スライシング
- アレイのスライシングはベクトルのスライシングの組み合わせ
ベクトルのスライシング(こちらを参考に)
- ベクトルのスライシングは２大原則
  - 「開始アドレス：終点アドレス：歩幅」の３整数で決める
  - アドレスは、-(len(v)) からlen(v)-1までの、2*len(v)個ある
- 「開始アドレス：終点アドレス：歩幅」
  - スライシングは３つの値を:でつなぐのが基本。始点アドレス、終点アドレス(その手前まで)、ステップ数の３つ
    - この第２要素の指定により「その手前まで」というのに、少し戸惑うけれど、「空ベクトルを返す」というときにd:d:*のようにうまく指定できる、という利点を思えば、そのようにするのがよい

v = arange(24) # 0,1,...,23の1次元np arrayを作る
v # このようにして全要素を取り出してもよいが、
v[0:len(v):1] # スライシングで同じようにする

- - ３つの値をつながないときは、「省略された」ことになる。ただし返ってくるのがアレイ形式かどうかはちょっと違う

v[3]
v[3:(3+1):1]
v[3:(3+1):1]
Out[32]: array([3])

v[3]
Out[33]: 3

v[3].shape
Out[34]: ()

v[3:(3+1):1].shape
Out[35]: (1,)

- (len(v)) から(len(v)-1)まで
  - スライシングにはデフォルト値がある
    - デフォルト値とはx:y:zと書くべきところ、x,y,zを省略することができて、その場合に使われる値のこと
    - x,y,zのデフォルト値は0,len(v),1
  - スライシングでは、アドレスに0-(len(v)-1)以外の値が使える
    - 使える範囲は、(-len(v))から(len(v)-1)

v = arange(24)
np.arange(-len(v),len(v))
v[np.arange(-len(v),len(v))]
np.arange(-len(v),len(v)-1)
Out[73]: 
array([-24, -23, -22, -21, -20, -19, -18, -17, -16, -15, -14, -13, -12,
       -11, -10,  -9,  -8,  -7,  -6,  -5,  -4,  -3,  -2,  -1,   0,   1,
         2,   3,   4,   5,   6,   7,   8,   9,  10,  11,  12,  13,  14,
        15,  16,  17,  18,  19,  20,  21,  22])
v[np.arange(-len(v),len(v))]
Out[74]: 
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9,
       10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23])

- - - それ以外のアドレスはだめ

v[-len(v)-1]
Traceback (most recent call last):

  File "<ipython-input-75-f6787182c348>", line 1, in <module>
    v[-len(v)-1]

IndexError: index out of bounds

v[len(v)]
Traceback (most recent call last):

  File "<ipython-input-77-dbef0a14a5bb>", line 1, in <module>
    v[len(v)]

IndexError: index out of bounds

- これを応用して、色々スライスする

v[21] # これはx:y:z型のスライシングではない
Out[93]: 21

v[21:24:1] # これはデフォルト値x:24:1を明示指定
Out[94]: array([21, 22, 23])

v[21::] # これは第２、第３のデフォルト値を省略
Out[96]: array([21, 22, 23])

v[21::1] # これは第２だけ省略
Out[97]: array([21, 22, 23])

v[21:24] # これは第３のデフォルト値を省略(:も省略)
Out[95]: array([21, 22, 23])

v[21:24:] # これは第３のデフォルト値を省略(:は残す)
Out[98]: array([21, 22, 23])

- ただし、逆順の場合は、デフォルト値がちょっと違う

v[::-1] # 逆順
Out[121]: 
array([23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10,  9,  8,  7,
        6,  5,  4,  3,  2,  1,  0])

v[23::-1] # 第１引数は23(またはそれより大きい値)が入っているのと同じ
Out[122]: 
array([23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10,  9,  8,  7,
        6,  5,  4,  3,  2,  1,  0])

v[:0:-1] # 第２の値は0だと0番地が入らず、-1にすると、次行のように空になる
Out[123]: 
array([23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10,  9,  8,  7,
        6,  5,  4,  3,  2,  1])

v[:-1:-1]
Out[124]: array([], dtype=int32)

- スライシングでうまくいくときはそれで、そうでなければ、番地ベクトルを作って与えるのがよい

v[[1,5,6,2]]
Out[125]: array([1, 5, 6, 2])

アレイに使う

d = [24,24,24]
a = np.array(np.arange(prod(d))).reshape(d)
a[21:24:2,[1,2],2::-1]

Out[155]: 
array([[[12122, 12121, 12120],
        [12146, 12145, 12144]],

       [[13274, 13273, 13272],
        [13298, 13297, 13296]]])

- np.whereを使ってスライシングする

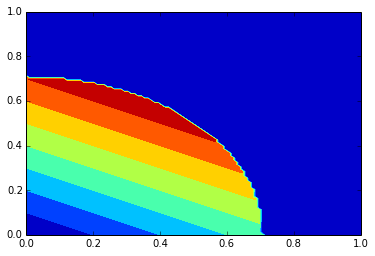
# 1次元グリッドを作る
n = 100
g1 = np.linspace(0,1,n)
# 2次元化する
# 2次元アレイを二つ作る。x座標を納めたアレイとy座標を納めたアレイ
g2_x,g2_y = meshgrid(g1, g1, sparse=True)
z = g2_x + g2_y * 2
# np.whereでスライシング
z[np.where(g2_x**2+g2_y**2 > 0.5)] = 0
mp.pyplot.contourf(g1,g1,z)