2014-10-30

共形変換複素関数 Holomorphic Harmonicのメモ

１変数(複素数)の複素関数を考える
台は複素平面(実数の二次元平面に見立てることができる)
関数の値は複素数。複素数は虚実の二成分からなるから、二次元平面上に二次元ベクトルが置いてあるようなものが得られる
二次元の台に二次元の値が乗っているので、４次元の世界の話になっている
ひとまず格子を作る

my.grid <- function(X=(-10):10,Y=(-10):10,n=200){
	x=seq(from=min(X),to=max(X),length=n+1)[-1]
	y=seq(from=min(Y),to=max(Y),length=n+1)[-1]
	as.matrix(rbind(expand.grid(x,Y),expand.grid(X,y)))
}
xy <- my.grid()
z <- xy[,1] + 1i * xy[,2]
plot(z,pch=20,cex=0.5)

ある関数 $f(z)=\frac{1}{z}$ に対応する共形変換を「グリッドの変形」で表せば

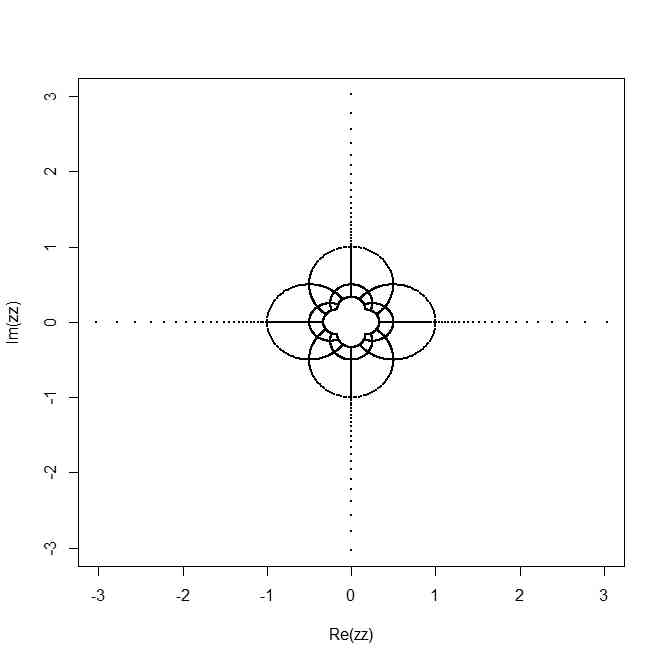
my.f <- function(z)1/z
zz <- my.f(z)
plot(zz,pch=20,cex=0.1,xlim=c(-3,3),ylim=c(-3,3))

ただし、複素平面上の点には、複素数〜二次元ベクトルが置かれているので、「ベクトル場」とみなせば

xy.2 <- as.matrix(expand.grid(rep(list(seq(from=-10,to=10,length=51)),2)))
z.2 <- xy.2[,1] + 1i * xy.2[,2]
zz <- my.f(z.2)
plot(Re(z),Im(z),col=gray(0.9),pch=20,cex=0.1)
col <- Mod(zz)
col2 <- col
col2[which(abs(col)==Inf)] <- 0
s <- order(col)
arrows(Re(z.2[s]),Im(z.2[s]),Re(z.2[s])+Re(zz[s]),Im(z.2[s])+Im(zz[s]),length=Mod(zz[s]),col=rgb(col2[s]/max(col2[s]),1-col2[s]/max(col2[s]),1))

今、共形変換では、共形変換を表す関数が複素平面上で「微分可能」であると言う。これは、ベクトル場で言えば、複素平面上に滑らかな移動を起こさせる場が存在していることと同じで、そのことから、ポテンシャルなどの概念で説明される物理現象に認められる諸性質が共形変換には備わっていることになる。そのような諸性質の一つがラプラス方程式だったりする
その諸性質を数学的に表現すると、「変換による角度の保存(直角は直角のまま→格子を変換すると線は曲がるが格子点で二本の線は直交する)、 $f(z)=az+b;a\ne=0,a.b \in \mathbf{C}$ という形で書ける(局所的に…?)、Analyticである、 $f(x,y)=u(x,y)+i v(x,y)$ というように虚実で関数を分離することができて、そのときに $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y},\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$ が成り立つ、これはholomorphicの定義でもある。また、この制約は結構厳しくて、共形変換である複素関数は限定的(であるが物理的に重要と思われているほぼすべての関数がそれに相当する？？)である。
また、この相互に制約のある $u(x,y),v(x,y)$ はHarmonic関数ともよばれ、 $u(x,y),v(x,y)$ は相互にHarmonic conjugateであるとも言う。 $\frac{\partial f(z)}{\partial \bar{z}=0$ という性質もあり、これをu,vの制約とみてもよいが、これは、共役複素数 $\bar{z}$ の方向に関して、偏微分が0、ということで、ベクトル場のベクトルの変化は、共役複素数方向に直交する方向に起きる、ということ(になるらしい)
また、微分可能なので、テイラー展開できる、という性質もあって、それを使って応用も広がる。さらに、２次元の話、級数展開の話、として考えると、二重周期性から楕円関数につながってもくる
特殊な例としては、関数の返り値が実数であるようなものだが、それは「平面にあるポテンシャル」のようなものである
複素平面の全域で何度でも微分可能であるとき、その関数は無限級数展開によって多項式とすることができ、そのような関数は、整関数。整関数の商として表せるのが有理型関数。そのような関数は、複素数が $r exp^{it}$ と書けることを思い出せば、三角関数・指数関数などを含むことがわかり、そのほか、ガンマ関数、ゼータ関数なども含まれる。ちなみに有理型関数は、整関数の射影とみることもできる(できそう)。

my.f <- function(z)log(Re(z)^2+Im(z)^2)
zz <- my.f(z)
s <- which(Mod(zz)!=Inf)
plot3d(Re(z[s]),Im(z[s]),zz[s])