球面の三角形二色塗り

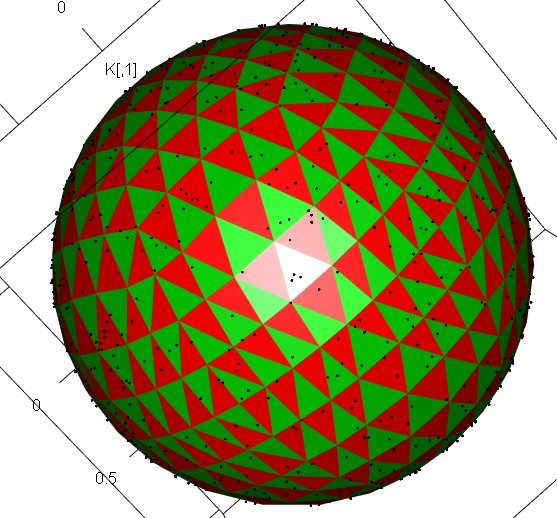
• 三角形で埋め尽くす。すべてのノードは次数が偶数
• 北極・南極の周りに６つの三角形を置く
• すべての頂点の次数を６にする
• すこしゆがむがまあまあになる
• そこから、三角形を３辺の中点で４分割していくと、そのような細かい分割ができる

theta <- (0:11)/12*2*pi
theta2 <- (0:5)/6*2*pi
equator <- cbind(cos(theta),sin(theta),rep(0,12))
north <- cbind(1/sqrt(2)*cos(theta2),1/sqrt(2)*sin(theta2),rep(1/sqrt(2),6))
south <- cbind(1/sqrt(2)*cos(theta2),1/sqrt(2)*sin(theta2),-rep(1/sqrt(2),6))
V <- rbind(c(0,0,1),north,equator,south,c(0,0,-1))
E <- rbind(cbind(rep(1,6),2:7),cbind(2:7,c(3:7,2)),cbind(rep(2:7,each=3),c(19,8,9,9,10,11,11,12,13,13,14,15,15,16,17,17,18,19)),cbind(8:19,c(9:19,8)),cbind(rep(20:25,each=3),c(19,8,9,9,10,11,11,12,13,13,14,15,15,16,17,17,18,19)),cbind(20:25,c(21:25,20)),cbind(rep(26,6),21:25))
n.pt <- 1000
K <- matrix(rnorm(n.pt*3),ncol=3)
K <- K/sqrt(apply(K^2,1,sum))
plot3d(K)

points3d(V,col=2,size=5)
for(i in 1:length(E[,1])){
	segments3d(V[E[i,],])
}

t <- seq(from=0,to=1,length=101)
tt <- cbind(t,1-t)
for(i in 1:length(E[,1])){
	tmp <- V[E[i,],]
	tmp2 <- tt %*% tmp
	tmp2 <- tmp2/sqrt(apply(tmp2^2,1,sum))
	points3d(tmp2,col=2)
}

tris <- rbind(c(1,2,3),c(1,3,4),c(1,4,5),c(1,5,6),c(1,6,7),c(1,7,2))
tris <- rbind(tris,c(2,8,9),c(2,3,9),c(3,9,10),c(3,9,11),c(3,4,11),c(4,11,12),c(4,12,13),c(4,5,13),c(5,13,14),c(5,14,15),c(5,6,15),c(6,15,16),c(6,16,17),c(6,7,17),c(7,17,18),c(7,18,19),c(7,2,19),c(2,19,8))

tris <- rbind(tris,c(20,8,9),c(20,21,9),c(21,9,10),c(21,9,11),c(21,22,11),c(22,11,12),c(22,12,13),c(22,23,13),c(23,13,14),c(23,14,15),c(23,24,15),c(24,15,16),c(24,16,17),c(24,25,17),c(25,17,18),c(25,18,19),c(25,20,19),c(20,19,8))

tris <- rbind(tris,c(26,20,21),c(26,21,22),c(26,22,23),c(26,23,24),c(26,24,25),c(26,25,20))

plot3d(K)
col <- rep(2:3,24)
for(i in 1:length(tris[,1])){
	triangles3d(V[tris[i,],],col=col[i])

}

my.partition.tris <- function(tri.x){
	tris <- tri.x$tris
	X <- tri.x$X
	col <- tri.x$col
	tris <- t(apply(tris,1,sort))
	pairs <- rbind(tris[,1:2],tris[,2:3],tris[,c(1,3)])
	pairs2 <- t(apply(pairs,1,sort))
	pairs2 <- unique(pairs)
	new.v <- (1:length(pairs2[,1])) + max(pairs2)
	new.X <- (X[pairs2[,1],] + X[pairs2[,2],] ) /2
	ret.X <- rbind(X,new.X)
	new.tris <- matrix(0,0,3)
	new.col <- c()
	for(i in 1:length(tris[,1])){
		tri.now <- tris[i,]
		tri.add1 <- which(pairs2[,1]==tri.now[1] & pairs2[,2]==tri.now[2])+ max(pairs2)
		tri.add2 <- which(pairs2[,1]==tri.now[2] & pairs2[,2]==tri.now[3])+ max(pairs2)
		tri.add3 <- which(pairs2[,1]==tri.now[1] & pairs2[,2]==tri.now[3])+ max(pairs2)
		
		tmp <- rbind(c(tri.now[1],tri.add1,tri.add3),c(tri.now[2],tri.add1,tri.add2),c(tri.now[3],tri.add2,tri.add3),c(tri.add1,tri.add2,tri.add3))
		new.tris <- rbind(new.tris,tmp)
		if(col[i]==1){
			tmp.col <- c(2,2,2,1)
		}else{
			tmp.col <- c(1,1,1,2)
		}
		new.col <- c(new.col,tmp.col)
	}
	new.tris <- t(apply(new.tris,1,sort))
	
	ret.X <- ret.X/sqrt(apply(ret.X^2,1,sum))
	return(list(tris=new.tris,X=ret.X,col=new.col))
}


init.tri.x <- list(tris=tris,X=V,col=c(1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1))

n.step <- 3
tri.x.list <- list()
tri.x.list[[1]] <- init.tri.x
for(i in 2:n.step){
	tri.x.list[[i]] <- my.partition.tris(tri.x.list[[i-1]])
}

for(i in 1:length(tri.x.list)){
	plot3d(K)
	n.Face <- length(tri.x.list[[i]]$tris[,1])
	col <- rep(2:3,n.Face/2)
	col <- c(rbind(tri.x.list[[i]]$col,tri.x.list[[i]]$col,tri.x.list[[i]]$col))
	tmp.ord <- c(t(tri.x.list[[i]]$tris))
	#for(j in 1:n.Face){
		#triangles3d(tri.x.list[[i]]$X[tri.x.list[[i]]$tris[i,],],col=col[j])
		triangles3d(tri.x.list[[i]]$X[tmp.ord,],col=col+1)

	#}	
	
}