遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

■

等高線 等値線 グラフ 等高線 等値線 グラフ
  • ２次元空間にベルヌーイ事象の確率関数が広がっているとする
  • その２次元空間で事象を観察すると、値0/1を持つ点が散在したデータが得られる
  • その点の２次元空間におけるドロネー図を描き、そのドロネー図グラフにおける点間距離を定める
  • そうすることで、各点は、0の点への距離分布と1の点への距離分布とが取れる
  • 0/1の点がまとまりを持っているならば、各点の0への点の距離の和と1の点への距離の和とは何かしらの情報を持つだろう
  • その２種類の距離和の比を点の属性として、色分けすると…

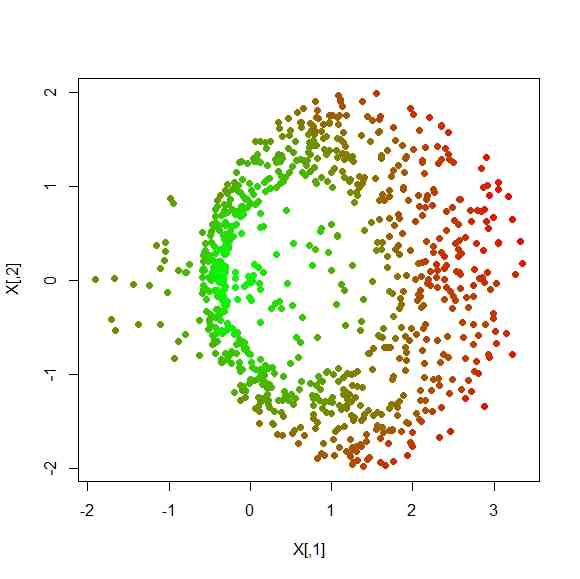
plot(X,col=rgb(len.ratio,1-len.ratio,0),pch=16)
library(quadprog)
library(geometry)
library(rgl)
library(gtools)
library(igraph)
library(vegan)

# 次元
d <- 2
# 点の数
n.pt <- 500
#X <- matrix(runif(n.pt*d)-0.5,n.pt,d)
# d次元座標
X <- matrix(rnorm(n.pt*d),ncol=d)
ss <- sample(1:n.pt,n.pt/3)
X <- X -0.1
X[ss,] <- X[ss,] + 0.4
n.pt0 <- 100
n.pt1 <- 750
#X0 <- cbind(rnorm(n.pt0,0,1),rexp(n.pt0,2))
#X0 <- cbind(rnorm(n.pt0,0,1),rnorm(n.pt0,2,1))
#X1 <- cbind(rexp(n.pt1,1),rnorm(n.pt1,2,2))
#X1 <- cbind(rnorm(n.pt1,1,1),rnorm(n.pt1,2,1))

#X0 <- cbind(rnorm(n.pt0,0,1),rep(0,n.pt0))
#X1 <- cbind(rnorm(n.pt1,5,1),rep(0,n.pt1))
t0 <- runif(n.pt0)
r0 <- runif(n.pt0)
X0 <- r0 * cbind(2*cos(t0*2*pi), 1*sin(t0*2*pi))
t1 <- runif(n.pt1)
r1 <- runif(n.pt1)+1
X1 <- r1 * cbind(cos(t1*2*pi)+0.7,sin(t1*2*pi))

X <- rbind(X0,X1)
n.pt <- n.pt0+n.pt1
Y <- Y.jit <- c(rep(0,n.pt0),rep(1,n.pt1))

#Y <- apply(X^0.3,1,sum)
#Y <- X[,1]^2+X[,2]^0.2
# 値のベクトル
#Y <- 1/(1+1/exp(X[,1]*2)) * 1/(1+1/exp(X[,2]*0.8))
#Y <- dnorm(sqrt(apply(X^2,1,sum)))
#Y <- 1/(1+1/exp((X[,1]+X[,2])*5))
# 乱雑項を入れる
#Y.jit <- Y + rnorm(n.pt,0,0.1)
## ベルヌーイ事象にする
#Y.jit <- rep(0,n.pt)
#for(i in 1:n.pt){
#	if(runif(1) < Y[i]){
#		Y.jit[i] <- 1
#	}
#}
#Y.jit <- Y + rnorm(n.pt,0,0.1)

plot3d(cbind(X,Y.jit))

# 値の面を描くためにドロネー分割する
d.X <- delaunayn(X)

# ドロネー分割は、三角形(四面体…)の頂点組を返すが
# そこから重複の無い辺リストを作る関数
ed.list.delaunay <- function(d.X){
	n <- length(d.X[1,])
	comb <- combinations(n,2)
	tmp <- matrix(0,0,2)
	for(i in 1:length(comb[,1])){
		tmp <- rbind(tmp,cbind(d.X[,comb[i,1]],d.X[,comb[i,2]]))
	}
	tmp <- as.data.frame(tmp)
	tmp <- unique(tmp)
	tmp
}
# ドロネー分割の重複の無い辺のリスト
ed.list <- ed.list.delaunay(d.X)

g <- graph.edgelist(as.matrix(ed.list))
sh <- shortest.paths(g)

ed.len <- sqrt(apply((X[ed.list[,1],] - X[ed.list[,2],])^2,1,sum))

len <- shortest.paths(g,weights=ed.len,mode="all")

len.0 <- apply(sh[,which(Y.jit==0)],1,sum)
len.1 <- apply(sh[,which(Y.jit==1)],1,sum)
len.ratio <- len.0/(len.0+len.1)
len.ratio <- (len.ratio-min(len.ratio))/(max(len.ratio)-min(len.ratio))
plot(X,col=Y.jit+1,pch=16)
plot(X,col=rgb(len.ratio,1-len.ratio,0),pch=16)
segments(X[ed.list[,1],1],X[ed.list[,1],2],X[ed.list[,2],1],X[ed.list[,2],2])