威嚇射撃に適した発射角度

• 銃を上空に向けて発射すると、弾がいつか落ちてくる。重力と空気抵抗について簡単な過程をして、どんな角度で撃つと着地時の速度が最も遅くなるかを調べてみよう、という話題がMIKUで扱われた

# g,k>0;gは重力加速度、kは空気抵抗を決める係数
# dvx(t)/dt = -kvx
# dvy(t)/dt = -g -kvy
# 初速度 V=(vx(0),vy(0))=v(cos(theta),sin(theta))とする(thetaは地面を0とした打ち出し角)
# vxは時刻∞で0に収束し、vyは時刻∞である速度vy(∞)に収束する(重力加速度と抵抗による加速度が釣り合う)
# それは以下のように表せて
# vx(t) = vx(0) e^(-kt)
# vy(t) = (vy(0)-vy(∞))e^(-kt) + vy(∞)
# vy(∞) = -g/k
# 地面からの高さ(鉛直位置座標)はintegral(0->T) vy(t) dt で
# (vy(0)-vy(∞))/k (1-e^(-kT)) + vy(∞)T
# 着地時刻は、(vy(0)-vy(∞))/k (1-e^(-kT)) + vy(∞)T = 0を解けばよい
# グラフを描こう
g <- 9.8
k <- 0.1
v <- 100
vy.inf <- -g/k
thetas <- seq(from=0,to=pi/2,length=20)
ts <- seq(from=0,to=30,length=1000)
VX <- VY <- V.abs <- Height <- matrix(0,length(thetas),length(ts))
for(i in 1:length(thetas)){
	vx0 <- v*cos(thetas[i])
	vy0 <- v*sin(thetas[i])
	VX[i,] <- vx0*exp(-k*ts)
	VY[i,] <- (vy0-vy.inf)*exp(-k*ts) + vy.inf
	Height[i,] <- (vy0-vy.inf)/k * (1-exp(-k*ts)) + vy.inf*ts
}
V.abs <- sqrt(VX^2+VY^2)

# 鉛直位置座標が最も0に近い時刻を求めておこう
land.time <- rep(0,length(thetas))
for(i in 1:length(thetas)){
	tmp.Height <- Height[i,]
	# 時刻0を排除する
	tmp.Height[1] <- max(abs(tmp.Height))
	tmp <- which(abs(tmp.Height)==min(abs(tmp.Height)))
	land.time[i] <- tmp[1]
}
# 上で求めた、着地相当時刻の速さを取り出す
v.land <- V.abs[cbind(1:length(thetas),land.time)]
# 着地相当時刻の速さが最も遅いのは？
tmp <- which(v.land==min(v.land))
print(thetas[tmp]/(2*pi)*360)
print("単位は度")

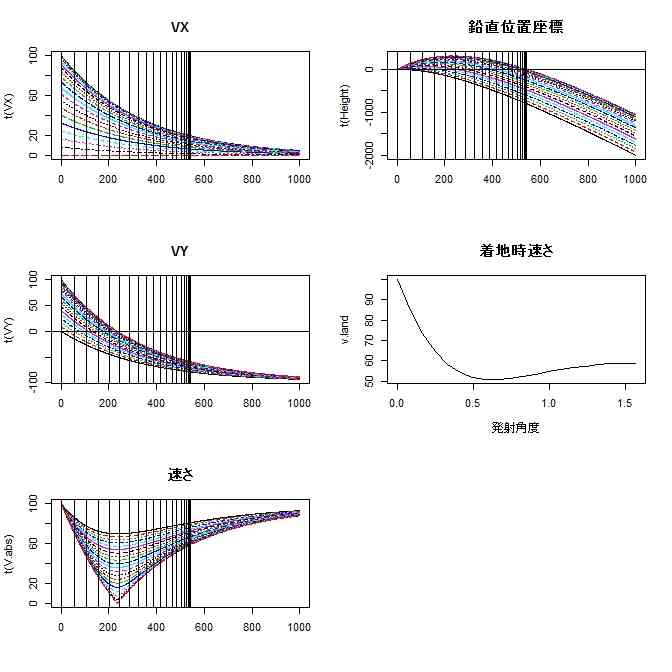
par(mfcol=c(3,2))
matplot(t(VX),type="l",main="VX")
abline(v=land.time)
matplot(t(VY),type="l",main="VY")
abline(v=land.time)
abline(h=0)
matplot(t(V.abs),type="l",main="速さ")
abline(v=land.time)
matplot(t(Height),type="l",main="鉛直位置座標")
abline(h=0)
abline(v=land.time)
plot(thetas,v.land,type="l",xlab="発射角度",main="着地時速さ")
par(mfcol=c(1,1))