内部点にフィボナッチ格子

• 昨日、移動に際して格子を使って移動ベクトルの一致性を指標にするにあたって内部点をドロネー集合にするとよさそうだが、面倒なのでただの乱点にする、という話を書いた
• ドロネー集合はフィボナッチ格子で作れる？
• それはcut & project?（こちら)
• ほとんど考えずに反射で多次元化してみる…
  • 1対(黄金比-1)を使った直線を引くのがよさそうなので、多次元の場合もそんな角度で立方格子を回転させてみる…(実際、ペンローズタイリングは黄金比を使った回転行列のようだ→こちら)
  • 元の高次元格子点数が稼げないので場合によってはまばらになるのだが…

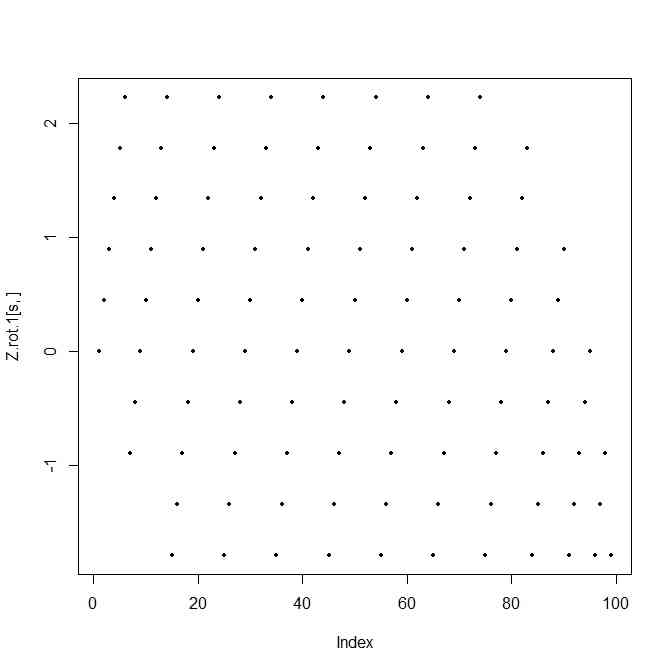
gdn.ratio <- (sqrt(5)-1)/2
gdn.ration.angle <- atan(gdn.ratio)
d <- 1

n <- 20
z <- 0:n

library(GPArotation)
R <- Random.Start(2*d)
nn <- 10
Imat <- R <- diag(rep(1,2*d))
gdn.mat <- matrix(c(cos(gdn.ration.angle),sin(gdn.ration.angle),-sin(gdn.ration.angle),cos(gdn.ration.angle)),2,2)
for(i in 1:nn){
	tmp <- Imat
	s <- sample(1:(2*d),2)
	tmp[s,s] <- gdn.mat
	R <- tmp %*% R
}
Z <- as.matrix(expand.grid(rep(list(z),2*d)))
Z.rot <- Z %*% R

Z.rot.1 <- matrix(Z.rot[,1:d],ncol=d)
Z.rot.2 <- matrix(Z.rot[,(1+d):(2*d)],ncol=d)
s <- which(apply(Z.rot.1^2,1,sum) < 5)
plot(Z.rot.1[s,],pch=20,cex=0.9)
d <- 2

n <- 20
z <- 0:n

library(GPArotation)
R <- Random.Start(2*d)
nn <- 100
Imat <- R <- diag(rep(1,2*d))
gdn.mat <- matrix(c(cos(gdn.ration.angle),sin(gdn.ration.angle),-sin(gdn.ration.angle),cos(gdn.ration.angle)),2,2)
for(i in 1:nn){
	tmp <- Imat
	s <- sample(1:(2*d),2)
	tmp[s,s] <- gdn.mat
	R <- tmp %*% R
}
Z <- as.matrix(expand.grid(rep(list(z),2*d)))
Z.rot <- Z %*% R

Z.rot.1 <- matrix(Z.rot[,1:d],ncol=d)
Z.rot.2 <- matrix(Z.rot[,(1+d):(2*d)],ncol=d)
s <- which(apply(Z.rot.1^2,1,sum) < 5)
plot(Z.rot.1[s,],pch=20,cex=0.9)

library(rgl)
d <- 3

n <- 10
z <- 0:n

library(GPArotation)
R <- Random.Start(2*d)
nn <- 100
Imat <- R <- diag(rep(1,2*d))
gdn.mat <- matrix(c(cos(gdn.ration.angle),sin(gdn.ration.angle),-sin(gdn.ration.angle),cos(gdn.ration.angle)),2,2)
for(i in 1:nn){
	tmp <- Imat
	s <- sample(1:(2*d),2)
	tmp[s,s] <- gdn.mat
	R <- tmp %*% R
}

Z <- as.matrix(expand.grid(rep(list(z),2*d)))
Z.rot <- Z %*% R

Z.rot.1 <- matrix(Z.rot[,1:d],ncol=d)
Z.rot.2 <- matrix(Z.rot[,(1+d):(2*d)],ncol=d)
s <- which(apply(Z.rot.1^2,1,sum) < 5)
library(rgl)

plot3d(Z.rot.1[s,],pch=20)