複素関数描図

• 複素平面は２次元
• 複素関数があって、のときにとなっているとすると、の４実数が登場する
• これを複素平面上に表すには
  • を「高さ」にしてを色にする、という方法と
  • ととの２つで色を作るが、実部と虚部のそれぞれのつながり具合・遠近具合が視覚的に『見えた』ように思わせる、という方法とが考えられる
• この記事は後者の話
• 色は「赤、青、黄色、緑」のようないわゆる「色相」と、その「明度」と「彩度」の３要素で捉えることができる
  • 「色相」は円環状にぐるりとできる(の値)
  • 「明度」は真っ暗な黒と明るいばかりの白とを２つの極端としてもつ(の値
  • 「彩度」も最もくすんだ黒と、最も鮮やかな色相ピカピカの色をとれての値
  • これを円錐や円柱として捉える事が出来る（HSVモデルと言う)(Wiki)
• 今、値という２次元の情報を持つ複素数を色相、明度、彩度の３つの値に対応づけることにする
  • 複素数を極座標表示して、その角度を「色相」に対応づける
  • 極座標表示のもう一つの成分である絶対値で明度と彩度を決める。ただし、絶対値の増減と明度・彩度のとの関係とを単調にすると、見えにくいので、等高線様にすることにする。等高線様にする、ということは、周期的に明度・彩度を変化させることで実現する。明度と彩度とのどちらかだけで周期性を出しても理論的にはよいのだろうが、そうすると、周期がそれほど視覚的に訴えないので、２つを合わせて使うことでより視覚的に情報が伝わりやすくしているのだと思われる。明度を最大値・最小値に固定した状態で彩度を変化させ、逆に彩度を最大値・最小値に固定した状態で明度を変化させる。明度・彩度はを取りうるがあまりに極端な値は見にくいので、見えやすい範囲を与えるのがよい

# zは複素数のベクトル
# int0,int1はintensityの上下限、sat0,sat1はSaturation(彩度)の上下限
my.hsv <- function(z,int0=0.6,sat0=0.3,int1=1,sat1=1){
# 複素数の偏角
	arg <- Arg(z)
	s <- which(arg<0)
	arg[s] <- arg[s]+2*pi
# 複素数の絶対値
	r <- Mod(z)
# 絶対値が非常に大きくてもそこそこの色になるように対数変換
	s <- which(r>1)
	r[s] <- log(r[s])
# 絶対値で周期性が出るように4のmod
	r. <- 4*(r%%1)
	k <- floor(r.)
	r. <- r.-k
# 明度が上限、明度が下限、彩度が上限、彩度が下限の４パターンを
# 4のmodに対応づける
# 明度・彩度を動かすときは、複素数の絶対値で１次線形変化
	inten <- sat <- rep(0,length(r))
	s <- which(k==0)
	inten[s] <- int1
	sat[s] <- sat1-(sat1-sat0)*r.[s]
	s <- which(k==1)
	inten[s] <- int1-(int1-int0)*r.[s]
	sat[s] <- sat0
	s <- which(k==2)
	inten[s] <- int0
	sat[s] <- sat1-(sat1-sat0)*(1-r.[s])
	s <- which(k==3)
	inten[s] <- int1-(int1-int0)*(1-r.[s])
	sat[s] <- sat1

	return(cbind(arg,inten,sat))
}

• 色には、HSVの他に３原色の混ぜ合わせであるrgbという表現がある
  • 色相、明度、彩度とrgbとの間には変換式がある(こちら)
  • ３原色でぐるりと１周できるように、偏角を6のmodで周回させる
  • 色相それ自体を３原色の１色の強さに反映させる。ただし、３原色のうちのどの色かは、ぐるりに合わせて変化させる
  • のこりの２色の値の高低は、色相ぐるりのための6のmodの余りの部分と明度と彩度をうまく組み合わせて、作る

my.hsv2rgb <- function(h,s,v){
# 色相の6 のmodでぐるりの情報を作る
	hi <- floor(h/(2*pi)*6)
	hi[which(hi==6)] <- 0
# 色相のぐるりの余りをfに入れ、それと明度・彩度とでp,q,tという３変数を決める
# ３変数を色相からの値を取らせる１つの原色を除いた２原色の値を定めるために使う
# 使い方は巡回させることでうまいことやる
	f <- (h/(2*pi)*6) %%1
	p <- v*(1-s)
	q <- v *(1-f*s)
	t <- v *(1-(1-f)*s)
	r <- g <- b <- rep(0,length(h))
	s <- which(hi==0)
		r[s] <- v[s];g[s] <- t[s]; b[s] = p[s];
	s <- which(hi==1)
		r[s] <- q[s];g[s] <- v[s]; b[s] = p[s];
	s <- which(hi==2)
		r[s] <- p[s];g[s] <- v[s]; b[s] = t[s];
	s <- which(hi==3)

		r[s] <- p[s];g[s] <- q[s]; b[s] = v[s];
	s <- which(hi==4)
		r[s] <- t[s];g[s] <- p[s]; b[s] = v[s];
	s <- which(hi==5)
		r[s] <- v[s];g[s] <- p[s]; b[s] = q[s];
	return(cbind(r,g,b))
}

x <- seq(from=-4,to=4,len=100)
xx <- expand.grid(x,x)
z <- xx[,1]+1i * xx[,2]

my.f <- function(z){
	(z^2-1)*(z-2-1i)^2/(z^2+2+2*1i)
}

w <- my.f(z)
hsv <- my.hsv(w,int0=0.1,sat0=0.1,int1=1,sat1=1)
col <- my.hsv2rgb(hsv[,1],hsv[,3],hsv[,2])

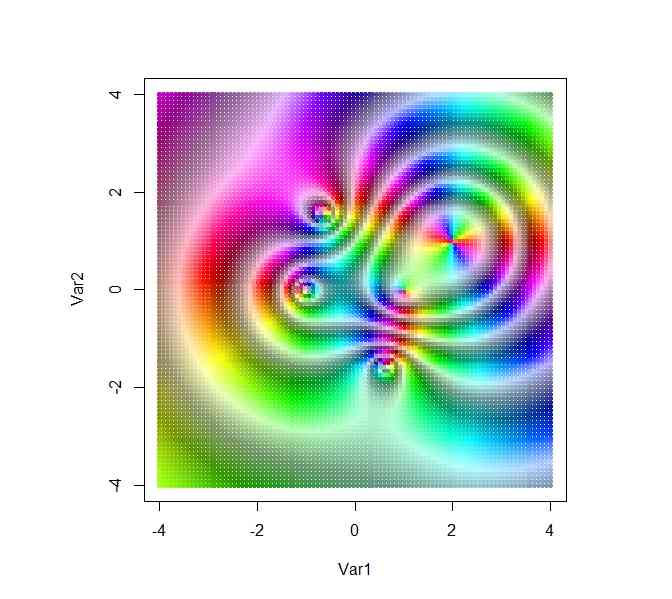
plot(xx,pch=20,col=rgb(col[,1],col[,2],col[,3]))

• 参考ページ１
• 参考ページ２
• [