
d <- 3
n.pt <- 2000
X <- matrix(rnorm(d*n.pt),ncol=d)
X <- X/sqrt(apply(X^2,1,sum))
librar(rgl)
plot3d(X)
nose <- X*0.3
nose[,1] <- nose[,1]+1
hoppe1 <- hoppe2 <- X* 0.3
theta <- pi/6
hoppe1[,1] <- hoppe1[,1] + cos(theta)
hoppe1[,2] <- hoppe1[,2] + sin(theta)
hoppe2[,1] <- hoppe2[,1] + cos(-theta)
hoppe2[,2] <- hoppe2[,2] + sin(-theta)
medama1 <- medama2 <- X * 0.1
phi1 <- pi/10
phi2 <- pi/8
medama1[,1] <- medama1[,1] + cos(phi1)*cos(phi2)
medama1[,2] <- medama1[,2] + sin(phi1)*cos(phi2)
medama1[,3] <- medama1[,3] + sin(phi2)
medama2[,1] <- medama2[,1] + cos(-phi1)*cos(phi2)
medama2[,2] <- medama2[,2] + sin(-phi1)*cos(phi2)
medama2[,3] <- medama2[,3] + sin(phi2)
plot3d(rbind(X,nose,hoppe1,hoppe2,medama1,medama2))
rgl.postscript("anpanman.eps","eps")
post.rot <- Anpanman
library(onion)
psi <- pi/3
u <- c(cos(phi1)*cos(phi2),sin(phi1)*cos(phi2),sin(phi2))
q <- quaternion(Re=cos(psi/2),i=sin(psi/2)*u[1],j=sin(psi/2)*u[2],k=sin(psi/2)*u[3])
q. <- Conj.onion(q)
for(ii in 1:length(Anpanman[,1])){
x <- quaternion(Re=0,i=Anpanman[ii,1],j=Anpanman[ii,2],k=Anpanman[ii,3])
tmp <- q*x*q.
post.rot[ii, ]<- c(i(tmp),j(tmp),k(tmp))
}
Max.a <- max(abs(c(Anpanman,post.rot)))
Anpanman. <- rbind(Anpanman,rep(Max.a,3))
Anpanman. <- rbind(Anpanman.,rep(-Max.a,3))
post.rot. <- rbind(post.rot,rep(Max.a,3))
post.rot. <- rbind(post.rot.,rep(-Max.a,3))
post.rot. <- post.rot. + 2.3
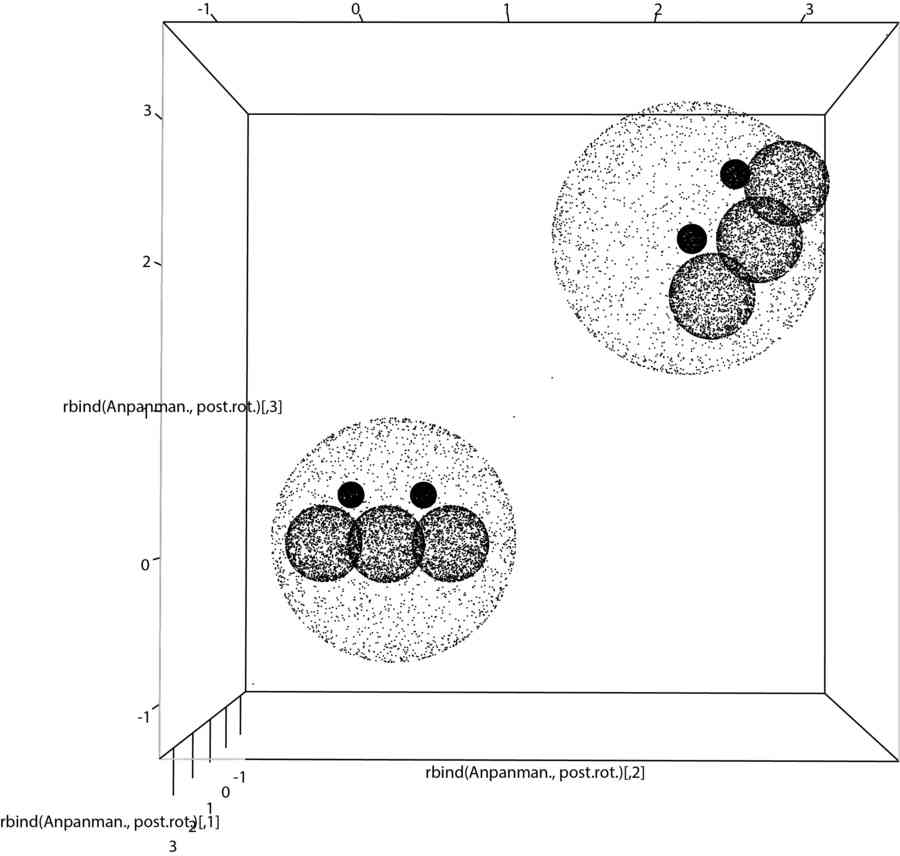
plot3d(rbind(Anpanman.,post.rot.))
rgl.postscript("anpanman2.eps","eps")
\subsubsection{複素数と四元数}
複素数は$i$は$i^2 = -1$を満足する虚数単位と2つの実数$a,b$を用いて
\begin{equation*}
z = a + i b
\end{equation*}
と表される数である。\\
四元数はこの虚数単位$i$のようなものをもう2種類($i,j,k$)使い、4つの実数$s,u,v,w$とともに表される数である。\\
\begin{equation*}
q = s + i u + j v + k w
\end{equation*}
$i,j,k$は次のような規則を持っている。
\begin{eqnarray*}
i^1=j^2=k^2=-1\\
ij =k,jk=i,ki=j\\
ji =-k,kj = -i, ik = -j
\end{eqnarray*}
この規則は以下のように行列状にすることもできる。
$ij$は第2行第3列に相当している。
\begin{table}[htb]
\begin{tabular}{|c|c|c|c|c|}\hline
& $-1$ & $i$ & $j$ & $k$ \\ \hline
$-1$ & $1$ & $-i$ & $-j$ & $-k$ \\ \hline
$i$ & $-i$ & $-1$ & $k$ & $-j$ \\ \hline
$j$ & $-j$ & $-k$ & $-1$ & $i$ \\ \hline
$k$ & $-k$ & $j$ & $-i$ & $-1$ \\ \hline
\end{tabular}
\end{table}
ここで、ある複素数$z=a+ib$に対して、共役複素数$\bar{z} = a-ib$を定めると、
\begin{equation*}
z \bar{z} = (a+ib)(a-ib)=a^2-iab+iab+b^2=a^2+b^2
\end{equation*}
という関係があって、
$|z|=\sqrt{a^2+b^2}=\sqrt{z\bar{z}}$という関係があった。
今、四元数についても同じようなことをする。
以下の話は、上の演算ルールを丁寧に適用すれば得られる結果なので、思い切って省略し、結果の便利さを紹介することにする。
ある四元数$q=s + iu + jv + kw$に対して共役四元数を$\bar{q}= s -(iu + jv + kw)$とすれば、$q\bar{q}=s^2+u^2+v^2+w^2$という関係が成り立つ。
\subsubsection{任意軸の回転}
いま、ある3次元ベクトル$\mathbf{p}$を回転軸として、ある3次元ベクトル$\mathbf{x}$を右ねじが進む方向に角$\psi$だけ回転させたときの回転後のベクトル$\mathbf{x'}$を求めたいとする。
実際、これをするのは面倒くさい。
それが四元数を次のように定めることで簡単に計算できる。\\
まず、3次元ベクトル$\mathbf{x},\mathbf{x'}$$(x,y,z),(x',y',z')$を、四元数
\begin{eqnarray*}
Q(x)=0 + ix + jy + kz\\
Q(x')=0+ix' + jy' + kz'
\end{eqnarray*}
に対応づける。
他方、回転軸$\mathbf{p}$の3成分$(p_x,p_y,p_z)$と回転角$\psi$とから、次のような四元数を定める。
\begin{eqnarray*}
q &= \cos{\frac{\psi}{2}} + \mathbf{p}\sin{\frac{\psi}{2}}\\
& = \cos{\frac{\psi}{2}} + \sin{\frac{\psi}{2}}(i p_x + j p_y + k p_z)
\end{eqnarray*}
このとき、次の式で得られる四元数の実数部分は0となり、非実数成分$i,j,k$が求める回転後の座標に対応している。
\begin{equation*}
Q(x') = q \times Q(x) \times \bar{q}\\
\end{equation*}
これを利用して、アンパンマンを回転させ、回転前後のアンパンマンを描くとこのようになる。

