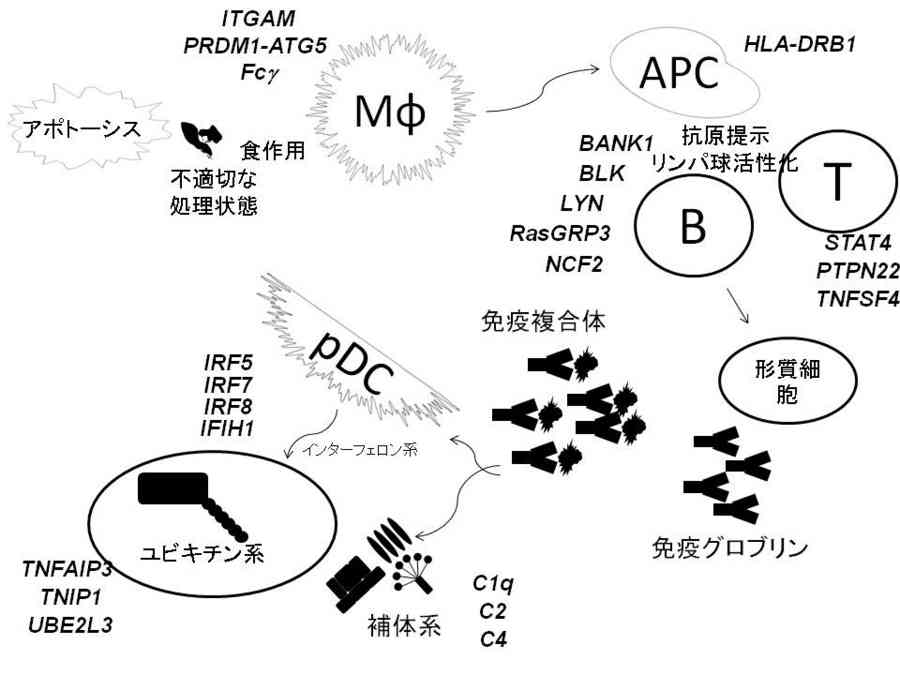
- マクロファージ・樹状細胞の絵を描きたい
- せっかくならRで描いてみよう
- 細胞は3次元だが、絵を描くときは2次元。細胞周縁はぐるりと回って戻ってきたときに、半径と傾きが一致していれば「つながる」
- やり方1
n.iter <- 40
n.pt <- 200
t <- seq(from = 0, to = 1, length = n.pt) * 2 * pi
t <- t[-1]
ippo <- (-0):1
r <- apply(matrix(sample(ippo,length(t)*n.iter,replace=TRUE),length(t),n.iter),1,sum)
k <- 5
K <- 10
R <- r*K
for(i in 2:k){
R <- R + r[c(k:length(r),1:(k-1))]*(K-(i-1))
}
R <- R/k
t.2 <- c(t,t[1])
R.2 <- c(R,R[1])
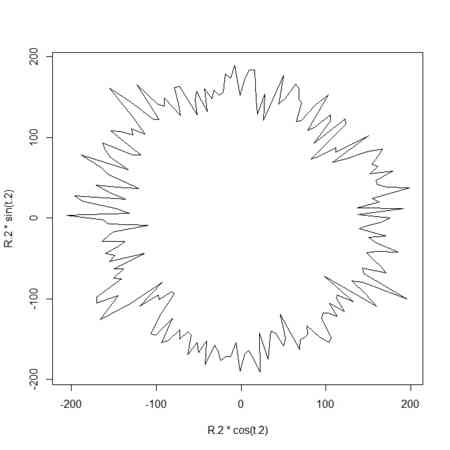
plot(R.2*cos(t.2),R.2*sin(t.2),type="l")
k <- 50
n.pt <- 2000
t <- seq(from = 0, to = 1, length = n.pt) * 2 * pi
t <- t[-1]
R <- rep(0,length(t))
for(i in 1:k){
R <- R+runif(1) * 10 * cos(t*sample(1:20,1)*2*pi+runif(1)*2*pi)
}
t.2 <- c(t,t[1])
R.2 <- c(R,R[1])
R.2 <- sd(R.2)*10+R.2 - min(R.2)
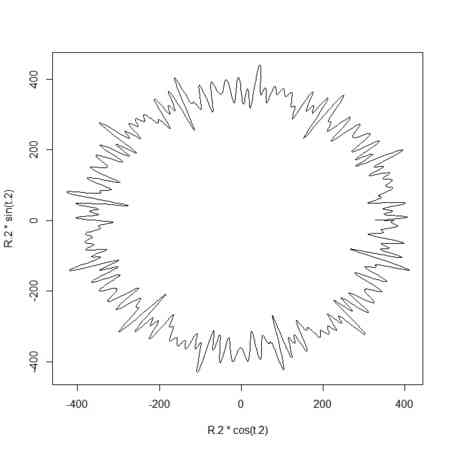
plot(R.2*cos(t.2),R.2*sin(t.2),type="l")
R <- rep(0,length(t))
ss <- rep(1,length(t))
s <- c(0,2*pi,runif(sample(3:8,1)) * 10-5)
for(j in 1:length(s)){
ss <- ss * (t-s[j])^2
}
R <- R + runif(1) * ss
t.2 <- c(t,t[1])
R.2 <- c(R,R[1])
R.2 <- (R.2 - min(R.2))/(max(R.2)-min(R.2))+1
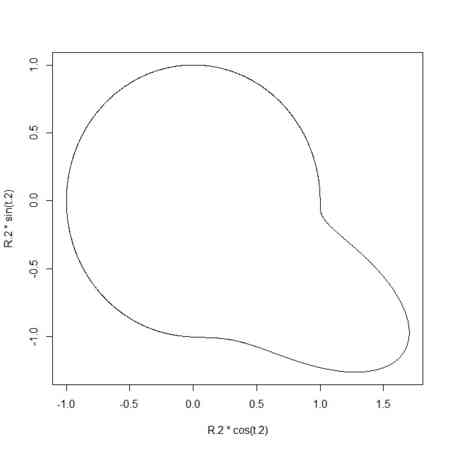
plot(R.2*cos(t.2),R.2*sin(t.2),type="l")



