2012-09-17

階層化したグラフ

グラフサブグラフ階層化 R

こちらで、知識をグラフ理論的に扱うために、グラフを階層化してみている
まず、ノードのリストが与えられる
個々のノードをシングル・ノードのサブグラフと考える
知識は、(シングル・ノードの)サブグラフを複数取り出してそのサブグラフにペアワイズな関係を与えること、そして、その知識を新規のサブグラフとして登録することであるとみなすことにする

Rで扱ってみよう

n <- 5

library(igraph)


init.whole <- function(n){
	ret <- list()
	for(i in 1:n){
		ret[[i]] <- list(v = i,e=NULL)
	}
	ret
}

w <- init.whole(n)

add.pair.relation <- function(w,u,v,type = 1,type.2 = 4){
	w[[length(w)+1]] <- list(v = c(u,v),e = list(m = matrix(c(u,v),nrow = 1), type = type),e.self = list(m = cbind(rep(length(w)+1,2),c(u,v)),type = type.2))
	w
}

add.relation <- function(w,vs,e.mat,type =1,type.2 = 5){
	w[[length(w)+1]] <- list(v = vs,e = list(m = e.mat, type = type),e.self = list(m = cbind(rep(length(w)+1,length(vs)),vs),type = type.2))
	w
}


w2 <- add.pair.relation(w,2,3)
w2

w3 <- add.pair.relation(w2, 4, 6, type = 2)
w3

w3[[7]]
tmp <- w3[[7]]
for(i in 1:length(tmp[[1]])){
	print(w3[[tmp[[1]][i]]])
}

w4 <- add.relation(w3, c(1,2,7), matrix(c(1,2,2,7),byrow=TRUE,ncol=2), type = 3)
w4
tmp <- w4[[8]]
for(i in 1:length(tmp[[1]])){
	print(w4[[tmp[[1]][i]]])
}

whole.e.mat <- NULL
e.col <- c()
for(i in 1:length(w4)){
	whole.e.mat <- rbind(whole.e.mat,w4[[i]]$e$m)
	e.col <- c(e.col, rep(w4[[i]]$e$type,length(w4[[i]]$e$m[,1])))
	whole.e.mat <- rbind(whole.e.mat, w4[[i]]$e.self$m)
	e.col <- c(e.col, rep(w4[[i]]$e.self$type,length(w4[[i]]$e.self$m[,1])))
}
whole.e.mat



my.plot.igraph <- function(g,v.col = 1, e.col = 1,cex = 2, pch = 19,v.name = NULL,text.dev = 0.1){
	# 座標決めルールの一つkamada.kawai法を用いることとする
	coords <- layout.kamada.kawai(g)
	# edge
	el.id <- get.edgelist(g)
	# グラフとして描く
	if(is.null(v.name)){
		v.name <- as.character(1:vcount(g))
	}
	#plot(g,layout = coords)

	# ノードの名前を文字列にするために別の方法をとる
	# ノードに色を付けよう
	#v.col <- rep(1,length(coords[,1]))
	plot(coords,cex = cex, pch = pch, col = v.col)

	# エッジを描く
	# エッジにも色を付けよう
	#e.col <- rep(1,length(el.id[,1]))
	segments(coords[el.id[,1],1],coords[el.id[,1],2],coords[el.id[,2],1],coords[el.id[,2],2], col = e.col)

	# 文字列を重ねる
	par(new =TRUE)
	# ノードから少しずらした位置に文字列を描かせる
	coords2 <- cbind(coords[,1],coords[,2]-text.dev)
	text(coords2,v.name,xlim = range(coords[,1]),ylim=range(coords[,2]))
}

g <- add.edges(graph.empty(length(w4)),c(t(whole.e.mat)))
#g <- graph.edgelist(whole.e.mat)
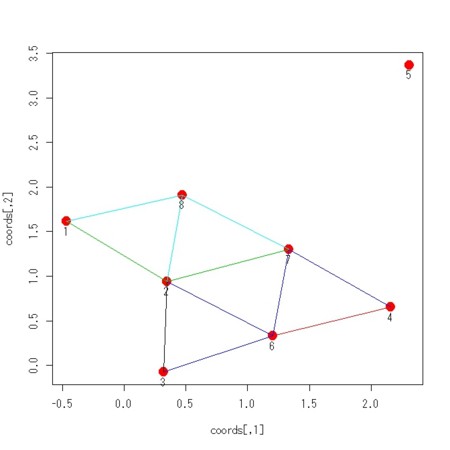
my.plot.igraph(g,v.col=2,e.col =e.col)

これは、結局、すべての「要素」がノードとなり、その間の関係をペアワイズにする仕組みではあるが、エッジの集合を取り扱えるようにしたものとも言える。また、そのエッジの集合を単位としてエッジに属性を与えることでもある
- サブグラフs1,s2,s3があったとき、新たなノードs4を加えるにあたって、「s4 は{s1,s2}のサブグラフ集合と関係する」という知識と「s4は{s1,s3}のサブグラフ集合と関係する」という知識とを与えることを考える
  - s4を新規ノードとして加え、s4->s1 s4->s2というエッジを与え、かつ、s4->s1,s4->s3というエッジを与えるとしよう
  - 結果として加わるのは、s4というノードとs4->s1, s4->s2,s4->s3の３本のエッジである
  - これでは与えた知識が劣化している
  - s4->s2が２本加わった、というようにエッジに重みを与えるにしても、知識は劣化している
  - 知識を劣化させないためには、(s4->s1,s4->s2)というエッジの集合の存在と(s4->s1,s4->s3)というエッジの集合の存在を分けて格納する必要がある
  - これは、(V={s4,s1,s2},E={s4->s1,s4->s2})というサブグラフと(V={s4,s1,s3},E={s4->s1,s4->s3})というサブグラフとを格納するという作業である