遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

Brownian mapについて勉強する

Brownian map
  • 球面上にランダムさが分布しているとはどういうことだろうか、という話
  • 第一資料はこちらを使う。『量子重力理論』とのかかわりが考えられるとか、広がりが大きそうな予感
  • まず、背景知識など
  • 平面グラフ
    • 四角形でできた平面グラフ(M_n^4と書いて、n個の四角形からできた平面グラフを表す)と木グラフとが一対一対応すること(Cori-Vauquelin-Schaeffer bijectionと呼ばれる関係)
      • 隣同士のノードの値の差が１か０になっている木グラフをWell-labeled treesと呼ぶ








    • 三角形分割と木グラフとの対応もある
      • この場合は、三角形分割はEulerian triangulationとなっていることが条件。このEulerian triangulationはすべての頂点の次数が偶数であるようなそれ
      • この場合は、２色に塗り分けられることが知られている
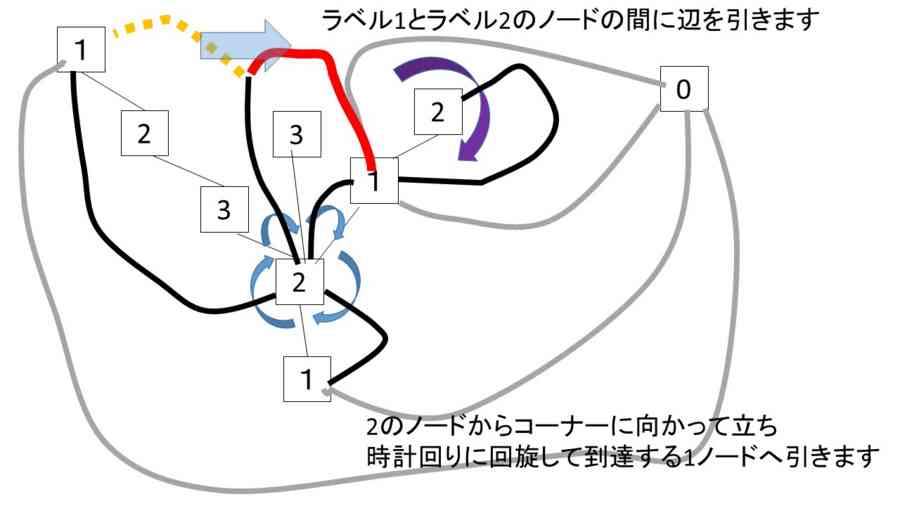
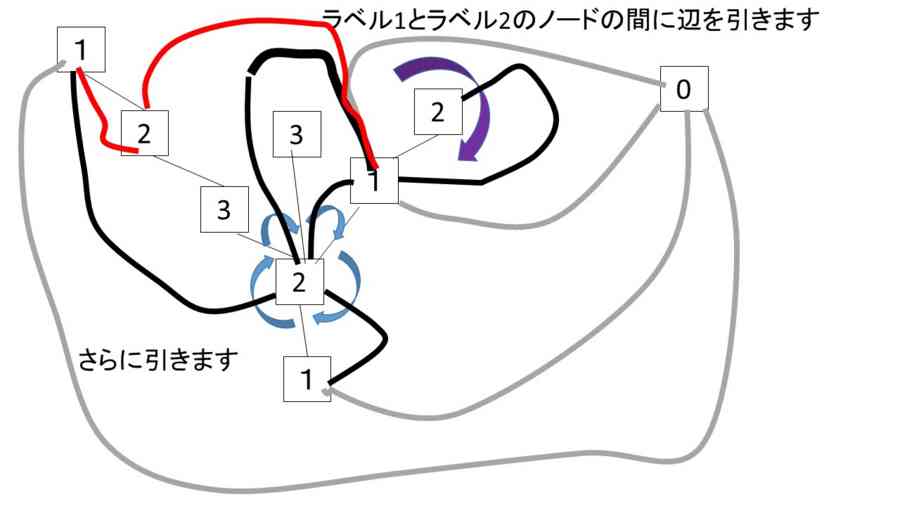
      • 今、２色に塗り分けられた三角形で敷き詰められた平面グラフ(Eulerian triangulation)があったとする。外周の１辺をとり、それに向きを決めることでグラフ全体のエッジに自然に向きを入れることができる
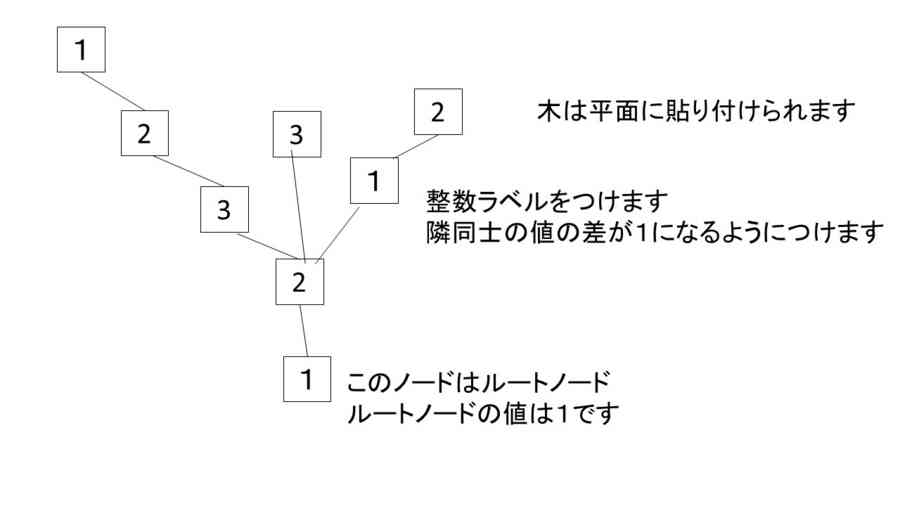
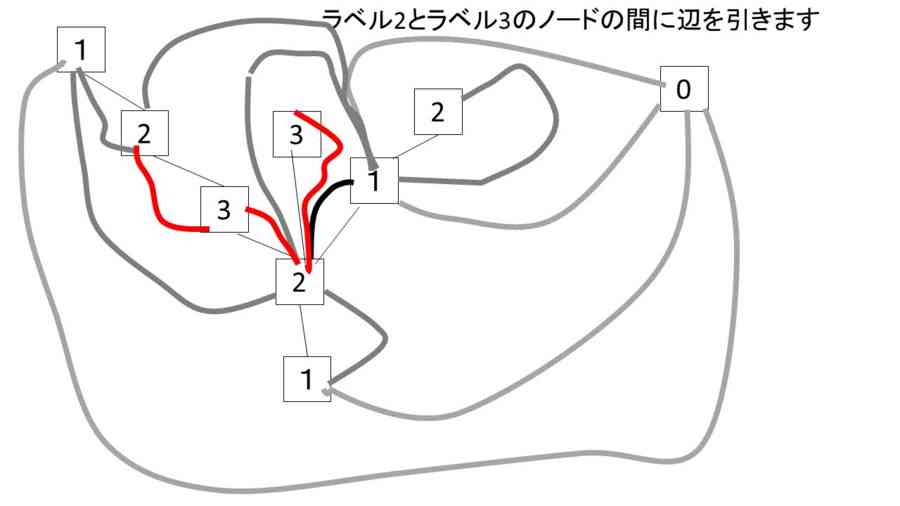
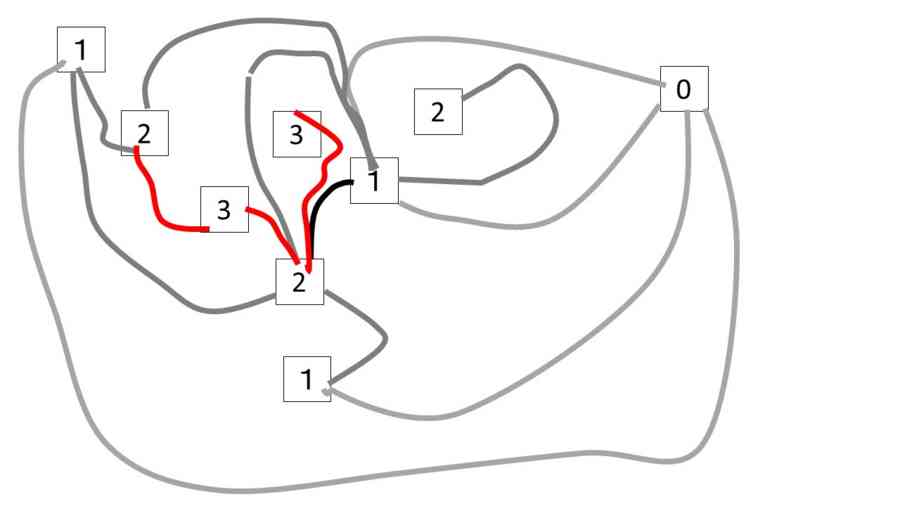
      • ここで初めに定めた辺の始点(ルートノード)からの距離をラベルとしてノードに与えると、すべての三角形にn,n+1,n+2というラベルがつく。ルートノードを含む三角形と同じ色の三角形について、n+1->n+2のエッジを取り出すと、それらは、木を成す。そして、そのノードには整数のラベルがついていて、隣り合うノードのラベルの値の差は必ず１である。これをEuler triangulationのWell-labeled treeという(ルートノードは取り去っておく)
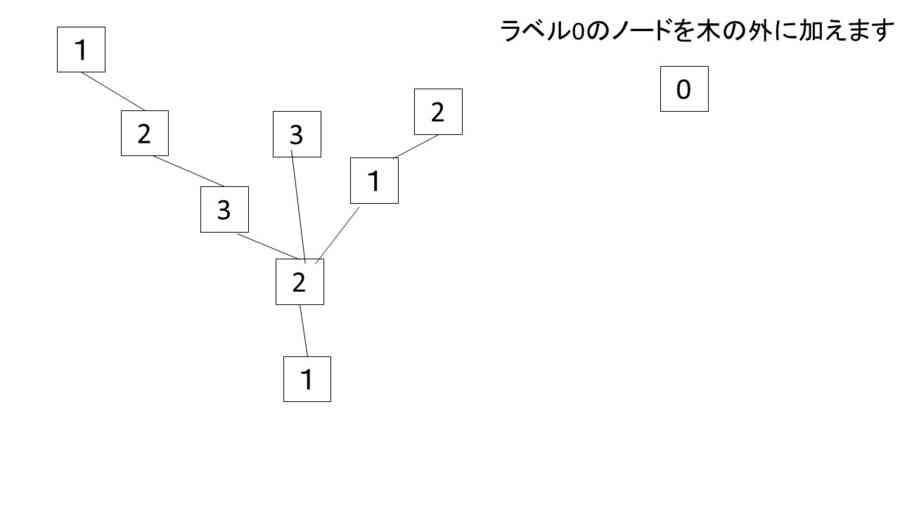
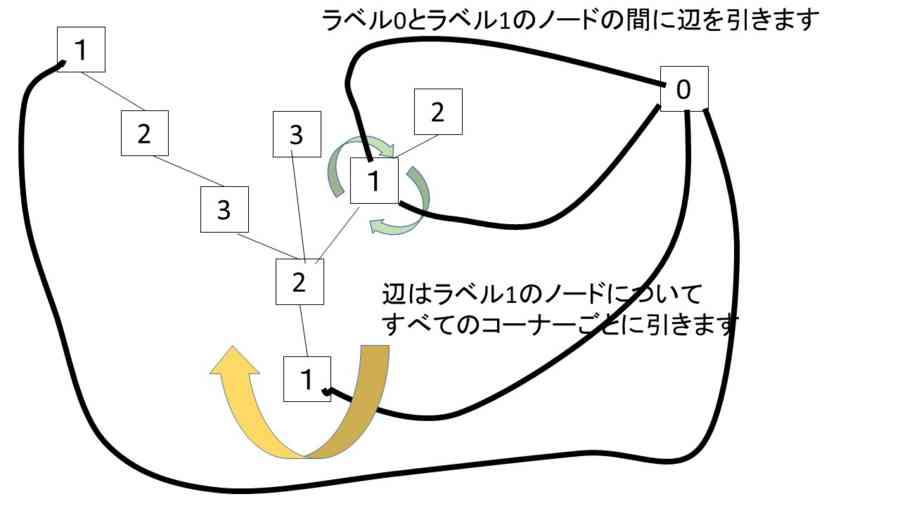
      • 今、Well-labeled treeがあったときに、すべてのエッジは、同色の三角形のn+1 -> n+2 の辺に相当しているので、nに相当するノードをその木から探して結べば、Well-labeled treeからEulerian triangulationが復元される。ルートノードを加える必要がある。三角形の復活に関して、塗り分け２色の片方であることから、探すべきnのノードはエッジの方向を考慮しながら、特定の領域にあるはずだ、という復元の仕方をしないといけないことに注意
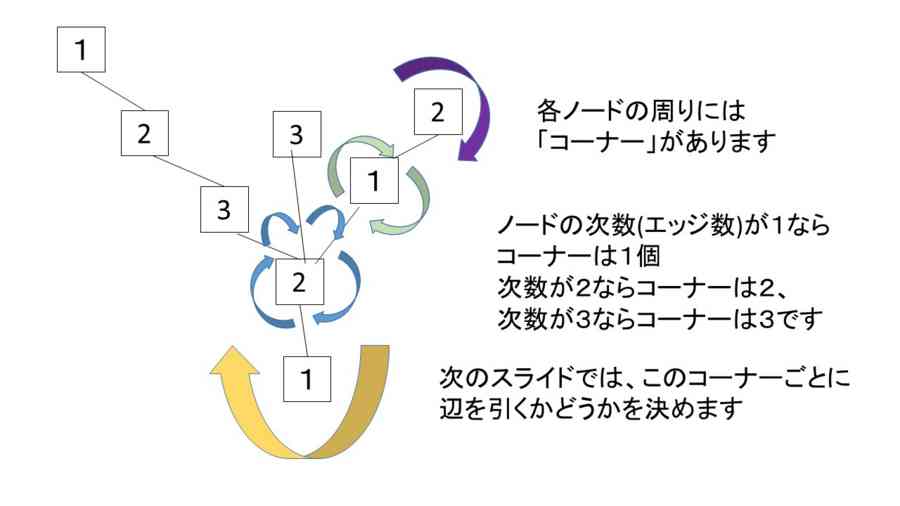
  • Eulerian TriangulationとWell-labeled treeを扱うにはPlanar graph特有の性質を使う必要がある。planar graph特有の性質とは、ノードに接続するエッジが周囲３６０度に関して順序があって、それを入れ替えたりできないこと。双対グラフを使うとそういう性質がハンドリングできるらしい→こちら
  • まったくの書きかけだけれど…(そして実装することがゴールではなく、どういう性質でどういうアルゴリズムなのかがわかることが目的だったので、実装自体はちょっとめんどくさそうだし、書きかけのままにするだろうけれど…)
    • Planar graphであるとき：
    • ハーフエッジを使うとよいかもしれない…と思う
    • 時計回り巡回をするのに、ノードにエッジを持たせて、その持たせ方に角度順序の情報を持たせるとうまくいくはず
    • さらには、ハーフエッジと時計回り巡回をすると、グラフに１個以上のサイクルができて、すべてのハーフエッジは一度だけどれかのサイクルに帰属する、という形にできるはず
    • Brownian treeとしてはDiffusion-limited aggregationとかにつながっている
# Planar graphではエッジが付着しているその順番が問題になる

library(igraph)
n <- 10

edge.list <- matrix(c(1,2),1,2)
for(i in 3:n){
	edge.list <- rbind(edge.list,c(sample(edge.list,1),i))
}
# ルートノードを挿入する
Rt <- n+1 # ルートノードのID
# lbが1->2のエッジの両端ノードとRtの間にエッジを入れる
# エッジをedge.orderのどこに入れるかでplanar graphとしての意味合いが決まる

edge.list.lb <- cbind(lb[edge.list[,1]],lb[edge.list[,2]])
edge.list.lb.sort <- t(apply(edge.list.lb,1,sort))
# 隣り合うエッジラベルの値は１違うだけなので、第１列の値を知れば、第２列の値はそれに１を加えた値である
# エッジラベルの大小の向きも大事
edge.list.lb.dir <- edge.list.lb[,1] < edge.list.lb[,2]
# エッジラベルの大小でソートしたエッジリスト(要素はノードID)
edge.list.sort <- edge.list
edge.list.sort[!edge.list.lb.dir,1] <- edge.list[!edge.list.lb.dir,2]
edge.list.sort[!edge.list.lb.dir,2] <- edge.list[!edge.list.lb.dir,1]

g <- graph.edgelist(edge.list)
plot(g)
ad.mat <- as.matrix(get.adjacency(g))

ad.mat2 <- ad.mat + (-1)*t(ad.mat)

rt <- sample(1:n,1)

lb <- shortest.paths(g,rt)+1
lb.2 <- c()
for(i in 1:n){
	lb.2[i] <- paste(i,lb[i],sep="_")
}
plot(g,vertex.label=lb)
pl.layout <- layout.auto(g)
plot(g, layout=pl.layout , vertex.label=lb)

edge.order <- edge.order.2 <- list()
for(i in 1:n){
	tmp <- neighbors(g,i,mode=3)
	tmp2 <- t(matrix(pl.layout[tmp,],ncol=2))-pl.layout[i,]
	angle <- Arg(tmp2[1,] + 1i*tmp2[2,])
	tmp3 <- tmp[order(angle)]
	edge.order[[i]] <- tmp[order(angle)]
	edge.order.2[[i]] <- rep(0,length(edge.order[[i]]))
	for(j in 1:length(edge.order[[i]])){
		ttmp <- abs(edge.list[,1] - i)+abs(edge.list[,2]-edge.order[[i]][j])
		if(length(which(ttmp==0))==1){
			edge.order.2[[i]][j] <- which(ttmp==0)[1]
		}else{
			ttmp <- abs(edge.list[,2] - i)+abs(edge.list[,1]-edge.order[[i]][j])
			edge.order.2[[i]][j] <- which(ttmp==0)[1]
		}
	}
}
plot(g, layout=pl.layout,vertex.label=lb.2)


# 対処するエッジを選ぶ
target.st <- 1 # 小さい方のラベルが1であるエッジを対象とする

target.edge <- which(edge.list.lb.sort[,1]==target.st)

target.edge.st <- edge.list.sort[target.edge,1]
target.edge.end <- edge.list.sort[target.edge,2]

# Rtノードへのエッジを入れます。

new.edge <- rbind(edge.list,cbind(rep(Rt,2*length(target.edge)),c(target.edge.st,target.edge.end)))
new.lb <- c(lb,0)
g2 <- graph.edgelist(new.edge,directed=FALSE)
plot(g2,layout=rbind(pl.layout,rep(max(pl.layout),2)),vertex.label=new.lb)
plot(g2,layout=rbind(pl.layout,c(min(pl.layout),max(pl.layout))))

new.edge.order <- edge.order
for(i in 1:length(target.edge)){
	tmp.st <- target.edge.st[i]
	tmp.end <- target.edge.end[i]
	tmp.id <- which(edge.order[[tmp.st]] == tmp.end)
	tmp.len <- length(edge.order[[tmp.st]])
	
	if(tmp.id==1){
		pre <- c()
		post <- edge.order[[tmp.st]][(tmp.id):tmp.len]
	}else if (tmp.id==tmp.len){
		pre <- edge.order[[tmp.st]][1:(tmp.id-1)]
		post <- edge.order[[tmp.st]][(tmp.id):tmp.len]
	}else{
		pre <- edge.order[[tmp.st]][1:(tmp.id-1)]
		post <- edge.order[[tmp.st]][(tmp.id):tmp.len]
	}
	new.edge.order[[tmp.st]] <- c(pre,Rt,post)
	tmp.id <- which(edge.order[[tmp.end]] == tmp.st)
	tmp.len <- length(edge.order[[tmp.end]])
	if (tmp.id==tmp.len){
		pre <- edge.order[[tmp.end]][1:(tmp.id)]
		post <- c()
	}else if(tmp.id==1){
		pre <- edge.order[[tmp.end]][1:(tmp.id)]
		post <- edge.order[[tmp.end]][(tmp.id+1):tmp.len]
	}else{
		pre <- edge.order[[tmp.end]][1:(tmp.id)]
		post <- edge.order[[tmp.end]][(tmp.id+1):tmp.len]
	}

	new.edge.order[[tmp.end]] <- c(pre,Rt,post)
}


n.step <- max(lb)-1

# planar graphでのノードの遠近関係は、普通に測ればグラフ上の距離だが
# めぐり方として、複数のエッジの採用の仕方に時計回り・反時計回りなどの優先順位を入れると、その大小関係は辞書式順序になる

# 以下ではノード1からの最短パスがノードのたどり方とエッジのたどり方の両方で出る
# 反時計回りのルールを入れれば、エッジの順序を比較するべき

# ラベルが2->3 なるエッジについて、ラベル=3のノードから時計回り優先で最初に到達できるラベル=1のノードを探し、2->3->1の三角形を作る
# より一般的に k->(k+1)なるエッジについて、ラベル=k+1のノードから時計回り優先で最初に到達できるラベル=k-1のノードを探し、k->(k+1)->(k-1)の三角形を作る
# 挿入するエッジは、k->(k+1)のエッジの前後に挿入する

# 二つのパスリストを見て

for(i in 2:n.step){
	target.st <- i
	target.edge <- which(edge.list.lb.sort[,1]==target.st)
	candidate.node <- which(lb == target.st-1)
	target.edge.st <- edge.list.sort[target.edge,1]
	target.edge.end <- edge.list.sort[target.edge,2]
	for(j in 1:length(target.edge)){
		tmp.path <- get.shortest.paths(g2,from=target.edge.end[j],t=candidate.node,output="both")
		
	}
}

dis.eg <- get.shortest.paths(g,1,output="both")