オーサグラフ

• 球面を平面に投影する仕組みとしてオーサグラフというやり方(商品)がある
• AuthaGraph オーサグラフ 世界地図こちらのサイト

• 球を正四面体に投影するというやり方で平面化する
• いかにも、真似して『やりたく』なるタイプの美しい方法である
• ３次元球の表面である２次元多様体を３次元空間の正単体に投影する
• k次元球の表面であるk-1次元多様体をk次元空間の正単体に投影する
• まず半径1の球上に頂点を持つ正単体の頂点座標を取る

# 正四面体の１つの面のみを考える
# nc-1 正単体(nc個の頂点)の頂点ベクトルを作る
CategoryVector<-
function (nc = 3) 
{
    df <- nc - 1
    d <- df + 1
    diagval <- 1:d
    diagval <- sqrt((df + 1)/df) * sqrt((df - diagval + 1)/(df - 
        diagval + 2))
    others <- -diagval/(df - (0:(d - 1)))
    m <- matrix(rep(others, df + 1), nrow = df + 1, byrow = TRUE)
    diag(m) <- diagval
    m[upper.tri(m)] <- 0
    as.matrix(m[, 1:df])
}
k<-3
v<-CategoryVector(k+1)

> v
           [,1]       [,2]       [,3]
[1,]  1.0000000  0.0000000  0.0000000
[2,] -0.3333333  0.9428090  0.0000000
[3,] -0.3333333 -0.4714045  0.8164966
[4,] -0.3333333 -0.4714045 -0.8164966

• 球面上の任意の点aの座標を定める

a<-rnorm(k)
a<-a/sqrt(sum(a^2))

> a
[1]  0.93590489 -0.06828931  0.34556996

• 点aと原点を通る直線が正四面体のそれぞれの面の３頂点の頂点ベクトルの線形結合として表す
• そのために４つの面を作る頂点の組み合わせを作る

v.id<-1:(k+1)
library(gtools)
surfaces<- combinations(k+1,k,v.id)

> surfaces
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    1    2    4
[3,]    1    3    4
[4,]    2    3    4

• 点aの座標をそれぞれの面の頂点ベクトルの線形結合にする
  • 

senkei<-function(a,V){
  M<-cbind(t(V),a)
  M<-rbind(M,c(rep(1,length(a)),0))
  solve(M,c(rep(0,length(a)),1))
}
b<-list()
for(i in 1:length(surfaces[,1])){
  b[[i]]<-senkei(a,v[surfaces[i,],])
}

> b
[[1]]
[1]  0.66637736  0.08256366  0.25105897 -0.59319042

[[2]]
[1] -98.04747  39.77801  59.26946 140.03912

[[3]]
[1]  0.8716950  0.2515812 -0.1232762 -0.8856955

[[4]]
[1] 0.3505316 0.2493642 0.4001042 0.3561615

> v[1,]*b[[1]][1]+v[2,]*b[[1]][2]+v[3,]*b[[1]][3]
[1]  0.55516982 -0.04050857  0.20498879
> a*b[[1]][4]
[1] -0.55516982  0.04050857 -0.20498879

• たくさんの点でやってみよう

Npt<-10000

Sp<-Sx<-matrix(0,Npt,k)


for(i in 1:Npt){
	a<-rnorm(k)
	a<-a/sqrt(sum(a^2))
	Sp[i,]<-a
	v.id<-1:(k+1)
	library(gtools)
	surfaces<- combinations(k+1,k,v.id)

	senkei<-function(a,V){
	  M<-cbind(t(V),a)
	  M<-rbind(M,c(rep(1,length(a)),0))
	  solve(M,c(rep(0,length(a)),1))
	}
	b<-matrix(0,length(surfaces[,1]),k+1)
	for(j in 1:length(surfaces[,1])){
	  b[j,]<-senkei(a,v[surfaces[j,],])
	}
	tmp<-apply((b>=0),1,prod)
	selected<-which(tmp==1)
	Sx[i,]<-t(v[surfaces[selected,],])%*%b[selected,1:k]
}

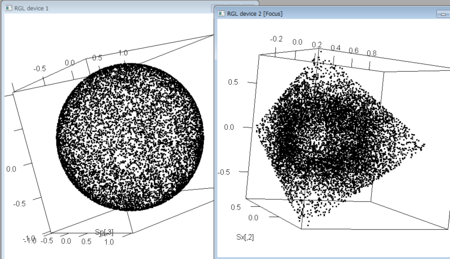
library(rgl)
plot3d(Sp)
open3d()
plot3d(Sx)