2014-01-04

複素数界に飛び出ている円軌道

円正単体 R

原点を中心とした半径１の円(単位円)と三角関数は表と裏の関係にある
この円を複素平面に描けば $e^{2\pi i x} = \cos{x} + i \sin{x}$ で表せる
$f(x)=\frac{\sin(x) +1}{2}$ とすると $0-1$ 区間を正弦関数形の周期変化をしているものを表現していることになる
その裏、 $1-f(x)$ も同様に $0-1$ で周期変化をしている
この変化を２カテゴリの比率の周期変化の「基本」とみなせば、三角関数は２カテゴリ比率の滑らかで周期的な変化を表した関数と見ることができる
２カテゴリの $(0,0)-(1,1)$ というのは頂点数２の正単体なので、これをkカテゴリに一般化して、それを表す関数を、正単体的な「三角関数」と「円」との一般化と考えることにする
k個の頂点を持つ正単体はk次元空間のk本の直交軸の単位ベクトルを位置座標とするk個の点を結んで作れる
このようなk個頂点をぐるりと回して別の頂点に移す動きは $k!$ 通りあるが、その動きの１つを取り出すこととする
そのような動きはkxk正方行列で表せる
kxk正方行列を固有値分解すれば、そのような動きを滑らかな動きの途中の点としてみなすことができるし、その動きを続けていれば、動きをk回繰り返すと元の状態に戻るから、周期動作である
このような「周期的」で「滑らかな」動きを「正単体的」な「円」軌道であり、その軌道を個々の変数の関数として表したものを「正単体的」な「三角関数」と呼ぶことにする
Rで実験してみる
いくつかの性質があるようだ
- k次元空間の単位球面上の動きであるようだ
- kの偶奇で性質が違うことはその一つのようだ

simplex.trigonometric <- function(d){
	M <- make.circular(c(2:d,1))
	eigen.out <- eigen(M)
	V <- eigen.out[[2]]
	U <- solve(V)
	lambdas <- as.complex(eigen.out[[1]])
	L <- d
	t <- seq(from=0,to=1,length=1000)*L
	X <- matrix(0,length(t),d)
	X[1,1] <- 1
	for(i in 2:length(t)){
		tmp <- V %*% diag(lambdas^t[i]) %*% U
		X[i,] <- tmp %*% X[1,]
	}
	X
}
library(igraph)
K.graph.coords <- function(d){
	g.adj <- matrix(1,d,d)
	diag(g.adj) <- 0
	g <- graph.adjacency(g.adj,mode="undirected")
	g.coords <- layout.kamada.kawai(g)
	g.ctr <- apply(g.coords,2,mean)
	g.coords.2 <- t(t(g.coords)-g.ctr)
	g.coords.2
}

simplex.trigono.2D <- function(d){
	X <- simplex.trigonometric(d)
	k.graph.coords <- K.graph.coords(d)
	ret <- t(t(k.graph.coords) %*% t((X)))
	return(list(X=X,coords.2d=k.graph.coords,X.2D=ret))
}

make.circular <- function(v){
	ret <- diag(rep(1,length(v)))
	ret[v,]
}

ds <- 2:20
Xs <- K.coords <- Xs.2D <- list()
for(i in 1:length(ds)){
	d <- ds[i]
	tmp <- simplex.trigono.2D(d)
	Xs[[i]] <- tmp[[1]]
	K.coords[[i]] <- tmp[[2]]
	Xs.2D[[i]] <- tmp[[3]]
}
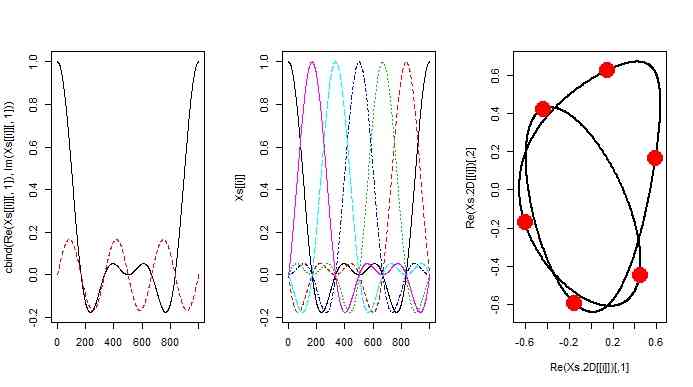
par(mfcol=c(1,3))
for(i in 1:length(ds)){
	matplot(cbind(Re(Xs[[i]][,1]),Im(Xs[[i]][,1])),type="l")
	matplot(Xs[[i]],type="l")
	par(ask=FALSE)

	plot(Re(Xs.2D[[i]]),cex=0.1,pch=20)
	points(Re(K.coords[[i]]),cex =5, col=2,pch=20)
	par(ask=TRUE)
}
par(mfcol=c(1,1))

その他のメモソース

CategoryVector<-function (nc = 3) 
{
    df <- nc - 1
    d <- df + 1
    diagval <- 1:d
    diagval <- sqrt((df + 1)/df) * sqrt((df - diagval + 1)/(df - 
        diagval + 2))
    others <- -diagval/(df - (0:(d - 1)))
    m <- matrix(rep(others, df + 1), nrow = df + 1, byrow = TRUE)
    diag(m) <- diagval
    m[upper.tri(m)] <- 0
    as.matrix(m[, 1:df])
}
# 使ってみる
CategoryVector(3)


d <- 3
Simplex.n <- function(d){
	diag(rep(1,d))
}
Simplex.n_1 <- function(d){
	X.0 <- CategoryVector(d)
	tmp.d <- sqrt(sum((X.0[1,]-X.0[2,])^2))
	X.0/tmp.d*sqrt(2)
}

Simplex.L <- function(d){
	sqrt(1/d)
}
Simplex.n.2 <- function(d){
	tmp <- Simplex.n_1(d)
	L <- Simplex.L(d)
	cbind(tmp,rep(L,d))
}
d <- 4
S.n <- Simplex.n(d)
S.n_1 <- Simplex.n_1(d)
S.L <- Simplex.L(d)
S.n.2 <- Simplex.n.2(d)

X <- simplex.trigonometric(d)

X.2 <- t(S.n.2 %*% t(X))
plot(X.2[,d],type="l")

X.3 <- X.2
X.3[,1] <- X.3[,1] - S.L
matplot(X.3,type="l")

library(rgl)
plot3d(Re(X.3[,1:3]),type="l")

X.0 <- CategoryVector(d)
tmp.d <- sqrt(sum((X.0[1,]-X.0[2,])^2))
X.1 <- X.0/tmp.d*sqrt(2)
tmp.d.2 <- sqrt(1/d)
X.2 <- cbind(X.1,rep(tmp.d.2,d))
apply(X.2^2,1,sum)