遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

割り付けるときと割り付けないとき。人数を増やす

割り付け R
  • 前の記事では、２人という限定した条件だった
  • 人数を任意にする
  • 計算がとたんに難しくなるので、単純な状況にする(こちらのような状況)
  • そうすると、「この関係が強そう」と思う程度を同じにしたまま、人数を増やすと、「素」で考えるのと比べて、その比が一度大きくなりつつ、比は小さくなり、ある値に収束するようだ
  • また、何人のときに「違いを表す比」が最大になるかは、「この関係が強そう」という程度が大きいほど、たくさんの「その他の人々」の存在時に最大になるようだ

Waritsuke<-function(k){
	ret<-matrix(0,k,k+1)
	ret[,1]<-1
	ret[,2]<-0
	f<-factorial(1:k)
	for(i in 2:k){
		for(j in 3:(i+1)){
			if(j==i+1){
				ret[i,j]<-f[i]-sum(ret[i,])
			}else{
				ret[i,j]<-f[i]/(f[j-1]*f[i-j+1])*ret[j-1,j]
			}
		}
	}
	ret
}

Waritsuke(k=10)

Waritsuke2<-function(k){
	ret<-matrix(0,k,k+1)
	ret[,1]<-1
	#ret[,2]<-0
	f<-factorial(1:k)
	for(i in 2:k){
		for(j in 2:(i+1)){
			if(j==i+1){
				ret[i,j]<-f[i]-sum(ret[i,])
			}else{
				ret[i,j]<-f[i]/(f[j-1]*f[i-j+1])*ret[j-1,j]
			}
		}
	}
	ret
}

Waritsuke2(k=5)

Waritsuke3<-function(k){
	ret<-matrix(0,k+1,k+1)
	ret[1,1]<-1
	f<-factorial(0:k)
	for(i in 2:(k+1)){
		for(j in 1:i){
			if(j==i){
				ret[i,j]<-f[i]-sum(ret[i,])
			}else{
				ret[i,j]<-f[i]/(f[j]*f[i-j+1])*ret[j,j]
			}
		}
	}
	ret
}
Waritsuke4<-function(k){
	ret<-matrix(0,k+1,k+1)
	ret[1,1]<-1
	#f<-factorial(0:k)
	g<-lgamma(1:(k+1))
	for(i in 2:(k+1)){
		for(j in 1:i){
			if(j==i){
				#ret[i,j]<-f[i]-sum(ret[i,])
				ret[i,j]<-exp(g[i])-sum(ret[i,])
			}else{
				#ret[i,j]<-f[i]/(f[j]*f[i-j+1])*ret[j,j]
				ret[i,j]<-exp(g[i]-(g[j]+g[i-j+1])+log(ret[j,j]))
			}
		}
	}
	ret
}
library(gtools)

probAllPermutation<-function(P,logarithm=TRUE){
	n<-nrow(P)
	if(!logarithm){
		P<-log(P)
	}
	perms<-permutations(n,n,1:n)
	np<-length(perms[,1])
	ret<-rep(0,np)
	for(i in 1:np){
		ret[i]<-sum(diag(P[perms[i,],]))
	}
	list(perms=perms,probs=ret)
}

CalcProbHx<-function(P,logarithm=TRUE){
	n<-nrow(P)
	p.out<-probAllPermutation(P,logarithm=logarithm)
	M<-matrix(0,n,n)
	for(i in 1:n){
		for(j in 1:n){
			selected<-which(p.out$perms[,i]==j)
			M[i,j]<-sum(exp(p.out$probs[selected]))
		}
	}
	list(perms=p.out$perms,probs=p.out$probs,prob.mat=t(M))
}

w<-Waritsuke3(k=5)

Seigo<-function(x,k){
	y<-(1-x)/(k-1)
	w<-Waritsuke4(k-1)
	P1<-P2<-0
	for(i in 0:(k-1)){
		P1<-P1+w[k,i+1]*y^i*x^(k-1-i)
		P2<-P2+w[k,i+1]*(y^i*x^(k-1-i)*i/(k-1) + y^(i+1)*x^(k-1-i-1)*(k-1-i)/(k-1) )
	}
	p1<-x*P1
	p2<-y*P2
	list(p1=p1,p2=p2)
}
SeigoLog<-function(x,k){
	y<-(1-x)/(k-1)
	logx<-log(x)
	logy<-log(y)
	w<-Waritsuke4(k-1)
	P1<-P2<-0
	for(i in 0:(k-1)){
		tmp1<-log(w[k,i+1])+i*logy+(k-1-i)*logx
		#P1<-P1+w[k,i+1]*y^i*x^(k-1-i)
		P1<-P1+exp(tmp1)
		tmp2.1<-log(w[k,i+1])+i*logy+(k-1-i)*logx-log(k-1)
		tmp2.2<-log(w[k,i+1])+(i+1)*logy+(k-1-i-1)*logx-log(k-1)
		P2<-P2+exp(tmp2.1)*i + exp(tmp2.2)*(k-1-i)
		#P2<-P2+w[k,i+1]*(y^i*x^(k-1-i)*i/(k-1) + y^(i+1)*x^(k-1-i-1)*(k-1-i)/(k-1) )
	}
	p1<-x*P1
	p2<-y*P2
	list(p1=p1,p2=p2)
}


Seigo2<-function(x,y,k){
	#y<-(1-x)/(k-1)
	w<-Waritsuke4(k-1)
	P1<-P2<-0
	for(i in 0:(k-1)){
		P1<-P1+w[k,i+1]*y^i*x^(k-1-i)
		P2<-P2+w[k,i+1]*(y^i*x^(k-1-i)*i/(k-1) + y^(i+1)*x^(k-1-i-1)*(k-1-i)/(k-1) )
	}
	p1<-x*P1
	p2<-y*P2
	list(p1=p1,p2=p2)
}
# k人のうちt人は当たっている確率を計算する
# t人の分はx^t
# 残りのk-tについて全員

k<-3
x<-0.9
y<-(1-x)/(k-1)

P1<-P2<-0
for(i in 0:(k-1)){
	P1<-P1+w[k,i+1]*x^i*y^(k-1-i)
	P2<-P2+w[k,i+1]*(x^i*y^(k-1-i)*(k-1-i)/(k-1) + x^(i-1)*y^(k-1-i+1)*i/(k-1) )
}

p1<-x*P1
p2<-y*P2

p1
p2

Seigo(x,k)


xx<-x
yy<-y
P<-matrix(c(xx,yy,yy,yy,xx,yy,yy,yy,xx),byrow=TRUE,k,k)
p.out<-probAllPermutation(P,logarithm=FALSE)
#p.out

calc.out<-CalcProbHx(P,logarithm=FALSE)
calc.out
exp(calc.out$probs)


ks<-2:10
ts<-seq(from=0.01,to=1-0.01,by=0.01)

P1s<-P2s<-matrix(0,length(ks),length(ts))
for(i in 1:length(ks)){
	for(j in 1:length(ts)){
		tmp<-Seigo(ts[j],ks[i])
		P1s[i,j]<-tmp$p1
		P2s[i,j]<-tmp$p2
	}
}

image(P1s/P2s)
 matplot(t(P1s/P2s),type="l")
ks<-seq(from=2,to=20,by=1)
#ks<-10^(0:3)+1
#ks<-c(2,3)
xy.ratios<-1.2^((-100):0)
#xy.ratios<-c(0.0001,0.01,0.1)
#xy.ratios<-1/seq(from=1,to=6,length=50)
preV<-postV<-P1s<-P2s<-P2multis<-Xvalue<-matrix(0,length(ks),length(xy.ratios))
Q1s<-Q2s<-Q2multis<-P1s
for(i in 1:length(ks)){
	for(j in 1:length(xy.ratios)){
		rr<-xy.ratios[j]
		Xvalue[i,j]<-1/(1+rr*(ks[i]-1))
		Q1s[i,j]<-Xvalue[i,j]
		Q2s[i,j]<-rr*Q1s[i,j]
		Q2multis[i,j]<-Q2s[i,j]*(ks[i]-1)
		tmp<-Seigo(Xvalue[i,j],ks[i])
		P1s[i,j]<-tmp$p1
		P2s[i,j]<-tmp$p2
		P2multis[i,j]<-P2s[i,j]*(ks[i]-1)
		preV[i,j]<-Xvalue[i,j]/(Xvalue[i,j]*(1+(ks[i]-1)*rr))
		postV[i,j]<-P1s[i,j]/(P1s[i,j]+(ks[i]-1)*P2s[i,j])
	}
}

image(P1s/P2s)
 matplot(1/t(P1s/P2s),type="l")
 matplot(1/t(P1s/P2multis),type="l")
 matplot(t(P1s/(P1s+P2multis)),type="l")
 image(P1s/(P1s+P2multis))

 
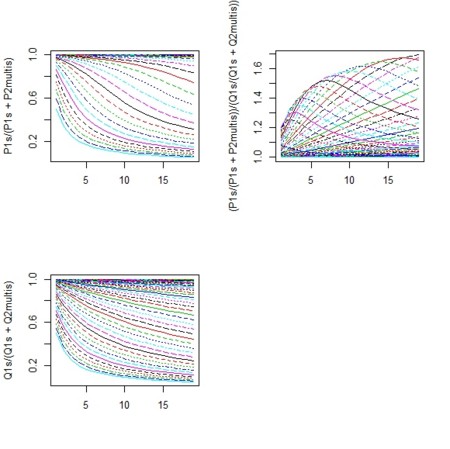
par(mfcol=c(2,2))
matplot(P1s/(P1s+P2multis),type="l")
matplot(Q1s/(Q1s+Q2multis),type="l")
matplot((P1s/(P1s+P2multis))/(Q1s/(Q1s+Q2multis)),type="l")
par(mfcol=c(1,1))

par(mfcol=c(1,2))
matplot(cbind(P1s/(P1s+P2multis),Q1s/(Q1s+Q2multis)),type="l")
matplot(cbind(P1s[,1]/(P1s[,1]+P2multis[,1]),Q1s[,1]/(Q1s[,1]+Q2multis[,1])),type="l")
par(mfcol=c(1,1))
par(mfcol=c(1,2))
matplot(log(cbind(P1s/(P1s+P2multis),Q1s/(Q1s+Q2multis))),type="l")
matplot(log(cbind(P1s[,1]/(P1s[,1]+P2multis[,1]),Q1s[,1]/(Q1s[,1]+Q2multis[,1]))),type="l")
par(mfcol=c(1,1))

 matplot((P1s/P2s),type="l")
 matplot((P1s),type="l")
 matplot((P2s),type="l")
matplot(t(P1s),type="l")
matplot(t(P2s),type="l")

plot(c(Xvalue),c(P1s/P2s))

plot(c(preV[,length(xy.ratios)]),c(postV[,length(xy.ratios)]),type="l")