離散と連続

• こちらで酔歩を使って、拡散律速凝集の話をしていた
• そのイントロで格子状酔歩と非格子状酔歩の話が出た
• 格子状に酔歩するときと格子点に限らず酔歩するときとの原点からの距離を比較する
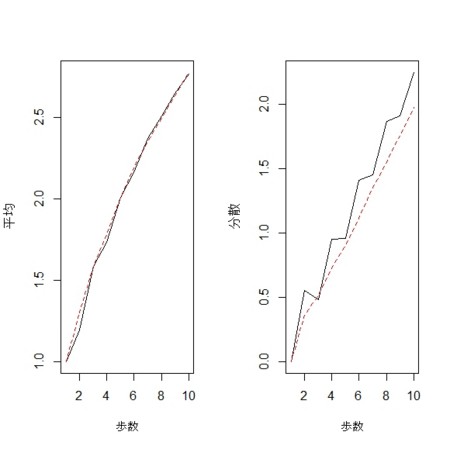
• 2次元、10歩のときは、離散的な影響が出て、分散ががたぼこする

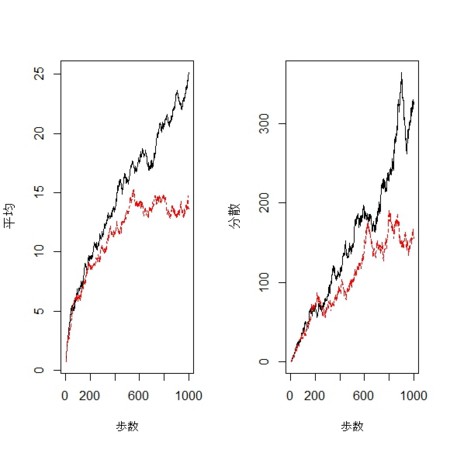
• 2次元、1000歩のときは、かなりの歩数を歩いてから、平均、分散の差が現れるようだ

# k 次元ランダムウォーク
# 格子状ウォークと非格子状ウォーク

# 全 n.f =  歩
# 1歩は距離 1
# １集計セットの試行回数 n.set =  回
# 集計の繰り返し数 n.iter =  回

k <- 2
n.f <- 1000
n.set <- 20
n.iter <- 1

# 集計繰り返しごとに、試行ごとに、各歩数のときの距離を格納する
d.koshi <- d.non.koshi <- array(0,c(n.f,n.set,n.iter))

# 格子状・非格子状ウォーク
suiho<- function(k,n.f,koshi){
	
	if(koshi){
		ret <- matrix(0,k,n.f)
		# 軸を選ぶ
		jiku.rand <- sample(1:k,n.f,replace=TRUE)
		# 軸について正負の向きを決める
		houkou.rand <- sample(c(-1,1),n.f,replace=TRUE)
		# 値を納めるべきretの番地(ベクトルとして)
		add <- jiku.rand + k*(0:(n.f-1))
		ret[add] <- houkou.rand
		ret <- t(ret)
	}else{
		# k次元正規分布は方向に関して一様ランダム
		ret <- matrix(rnorm(k*n.f),ncol=k)
		# 長さを１にそろえる
		ret <- ret/sqrt(apply(ret^2,1,sum))
	}
	ret <- apply(ret,2,cumsum)
	return(ret)
}

for(i.iter in 1:n.iter){
	for(i.set in 1:n.set){
		for(i.f in 1:n.f){
			koshi <- suiho(k,n.f,koshi=TRUE)
			non.koshi <- suiho(k,n.f,koshi=FALSE)
			d.koshi[,i.set,i.iter] <- sqrt(apply(koshi^2,1,sum))
			d.non.koshi[,i.set,i.iter] <- sqrt(apply(non.koshi^2,1,sum))
		}
	}
}

mean.d.koshi <- apply(d.koshi[,,1],1,mean)
mean.d.non.koshi <- apply(d.non.koshi[,,1],1,mean)

var.d.koshi <- apply(d.koshi[,,1],1,var)
var.d.non.koshi <- apply(d.non.koshi[,,1],1,var)

par(mfcol=c(1,2))
plot(mean.d.koshi,mean.d.non.koshi,main="平均",xlab="格子",ylab="非格子")
abline(0,1,col=2)
plot(var.d.koshi,var.d.non.koshi,main="分散",xlab="格子",ylab="非格子")
abline(0,1,col=2)

matplot(cbind(mean.d.koshi,mean.d.non.koshi),type="l",xlab="歩数",ylab="平均")
matplot(cbind(var.d.koshi,var.d.non.koshi),type="l",xlab="歩数",ylab="分散")