2011-12-27

Rで組み合わせ理論　Rで数学の色々をいじってみる

R 数学

$_n C_i = \begin{pmatrix} n \\ i \end{pmatrix}=\frac{n!}{i! (n-i)!}$

n<-10
i<-3
choose(n,i)
lchoose(n,i) # 指数対応で大きな数でも計算ができるように
exp(lchoose(n,i))
# n!の計算ができればよいので
factorial(1:10)
# これも指数化
lfactorial(1:10)
exp(lfactorial(1:10))
# n! = gamma(n+1)のガンマ関数を使う
factorial(1:10)
gamma(2:11)
# これも指数化
lgamma(2:11)
exp(lgamma(2:11))
# choose()をlgamma()で
choose(n,i)
exp(lgamma(n+1)-lgamma(i+1)-lgamma(n-i+1))

> n<-10
> i<-3
> choose(n,i)
[1] 120
> lchoose(n,i) # 指数対応で大きな数でも計算ができるように
[1] 4.787492
> exp(lchoose(n,i))
[1] 120
> # n!の計算ができればよいので
> factorial(1:10)
 [1]       1       2       6      24     120     720    5040   40320  362880 3628800
> # これも指数化
> lfactorial(1:10)
 [1]  0.0000000  0.6931472  1.7917595  3.1780538  4.7874917  6.5792512  8.5251614
 [8] 10.6046029 12.8018275 15.1044126
> exp(lfactorial(1:10))
 [1]       1       2       6      24     120     720    5040   40320  362880 3628800
> # n! = gamma(n+1)のガンマ関数を使う
> factorial(1:10)
 [1]       1       2       6      24     120     720    5040   40320  362880 3628800
> gamma(2:11)
 [1]       1       2       6      24     120     720    5040   40320  362880 3628800
> # これも指数化
> lgamma(2:11)
 [1]  0.0000000  0.6931472  1.7917595  3.1780538  4.7874917  6.5792512  8.5251614
 [8] 10.6046029 12.8018275 15.1044126
> exp(lgamma(2:11))
 [1]       1       2       6      24     120     720    5040   40320  362880 3628800
> # choose()をlgamma()で
> choose(n,i)
[1] 120
> exp(lgamma(n+1)-lgamma(i+1)-lgamma(n-i+1))
[1] 120

順列 $_n P_i=\frac{n!}{i!}$
全組合せ・全順列

> library(gtools)
> combinations(4,2)
     [,1] [,2]
[1,]    1    2
[2,]    1    3
[3,]    1    4
[4,]    2    3
[5,]    2    4
[6,]    3    4
> permutations(4,2)
      [,1] [,2]
 [1,]    1    2
 [2,]    1    3
 [3,]    1    4
 [4,]    2    1
 [5,]    2    3
 [6,]    2    4
 [7,]    3    1
 [8,]    3    2
 [9,]    3    4
[10,]    4    1
[11,]    4    2
[12,]    4    3

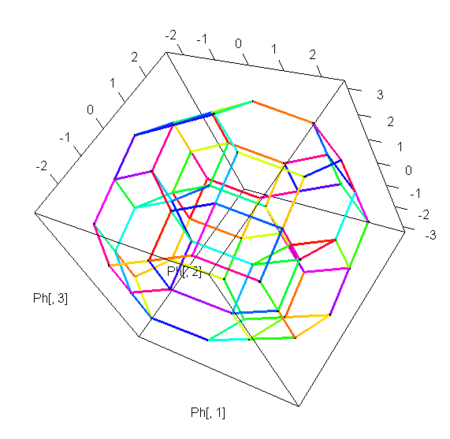
順列の空間配置 permutohedron (Wiki) を図にしてみる

#library(sphere) # CategoryVector()を有する私的パッケージ
CategoryVector<-
function (nc = 3) 
{
    df <- nc - 1
    d <- df + 1
    diagval <- 1:d
    diagval <- sqrt((df + 1)/df) * sqrt((df - diagval + 1)/(df - 
        diagval + 2))
    others <- -diagval/(df - (0:(d - 1)))
    m <- matrix(rep(others, df + 1), nrow = df + 1, byrow = TRUE)
    diag(m) <- diagval
    m[upper.tri(m)] <- 0
    as.matrix(m[, 1:df])
}

N<-5 # 大きい数字だと、重くなるのは当然…
X<-CategoryVector(N)
library(gtools)
p<-permutations(N,N)

Ph<-p%*%X

library(rgl)
# N-2要素が一致している順列ペアを確認し、辺を描かせる
# 辺数調べの最大値制約を入れる
Emax<-1000000
Ecounter<-0
E<-NULL
DifID<-NULL
for(i in 1:(length(p[,1])-1)){
	for(j in (i+1):length(p[,1])){
		tmp<-p[i,]-p[j,]
		Ecounter<-Ecounter+1
		if(length(which(tmp==0))==N-2 & length(which(abs(tmp)==1))==2){
			E<-rbind(E,Ph[i,])
			E<-rbind(E,Ph[j,])
			DifID<-rbind(DifID,sort(which(abs(tmp)==1)))
		}
		if(Ecounter==Emax){
			break
		}
		
	}
	if(Ecounter==Emax){
			break
		}
}
plot3d(Ph[,1],Ph[,2],Ph[,3])

# 異なる順列位置によって辺の色を変える
C<-DifID%*% matrix(c(1,N+1),2,1)

segments3d(E[,1:3],col=rainbow(C),lwd=3)