ベッセル関数・非心カイ分布 - ryamadaのコンピュータ・数学メモ

一昨日の記事で正・非心カイ分布・カイ二乗分布の密度関数をベッセル関数・超幾何関数を用いて描き、その相互関係を確認した。
式変形をきちんとしているのか、不安なので、検算をすることにする
4つの密度関数を並べ直してみよう
カイ分布
- $f(x,k)=2\frac{1}{\Gamma(\frac{k}{2})} 2^{-\frac{k}{2}} x^{k-1}e^{-\frac{x^2}{2}}$
カイに乗分布
- $F(y=x^2,k)=\frac{1}{\Gamma(\frac{k}{2})}2^{-\frac{k}{2}}y^{\frac{k}{2}-1}e^{-\frac{y}{2}}$
- $F(y=x^2,k) = \frac{1}{2\sqrt{y}} f(x,k)$
非心カイ分布
- $g(x,k,m) = \{I_{\frac{k}{2}-1}(mx)\}(\frac{x}{m})^{\frac{k}{2}}me^{-\frac{x^2+m^2}{2}}$
非心カイ二乗分布
- $G(y=x^2,k,M=m^2) = \frac{1}{2}\{I_{\frac{k}{2}-1}(\sqrt{My})\}(\frac{y}{M})^{\frac{k}{4}-\frac{1}{2}}e^{-\frac{y+M}{2}}$
- $G(y=x^2,k,M=m^2) = \frac{1}{2\sqrt{y}} g(x,k,m)$
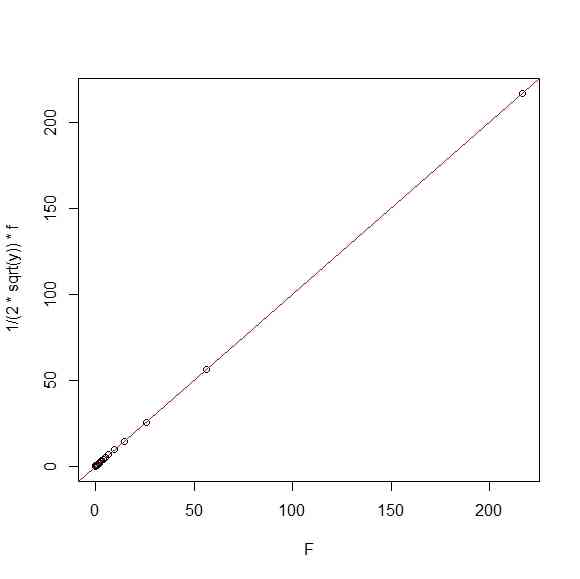
正心カイ分布と正心カイ二乗分布の関係 $F(y=x^2,k) = \frac{1}{2\sqrt{y}} f(x,k)$ を確かめてみる

x <- seq(from=0,to=10,by=0.01)
y <- x^2
df <- runif(1)*5
F <- dchisq(y,df)
f <- 2/gamma(df/2)*2^(-df/2)*x^(df-1)*exp(-x^2/2)
plot(F,1/(2*sqrt(y))*f)
abline(0,1,col=2)

非心カイ分布と非心カイ二乗分布の関係を確かめてみる
- Rでベッセル関数はパッケージ"Bessel"(ベッセルの第１種関数はBesselI())

# dchisq()とBesselI()を使ったカイ二乗分布の一致を確認
x <- seq(from=0,to=10,by=0.01)
y <- x^2
df <- runif(1)*5
m <- runif(1)*5
M <- m^2
G <- dchisq(y,df,M)
G2 <- 1/2*BesselI(sqrt(y*M),df/2-1)*(y/M)^(df/4-1/2)*exp(-(y+M)/2)
plot(G,G2)
abline(0,1,col=2)

- ベッセル関数を使って非心カイ分布

# BesselI()を使って非心カイ分布
g2 <- (x/m)^(df/2)*m*exp(-(x^2+m^2)/2)*BesselI(m*x,df/2-1)
plot(x,g2)
# dchisq()を使って非心カイ分布
g <- G*2*x
plot(g,g2)
abline(0,1,col=2)

期待値
- 正心カイ二乗分布の期待値はdf
- 非心カイ二乗分布の期待値はdf+M
- 正心カイ分布の期待値は
- 非心カイ分布の期待値は
  - ただし、 $L_n^{(\alpha)}(x)$ はLaguerre polynomialsと呼ばれるもので、(ありがたいことに超幾何関数の計算関数を書いておいた(昨日-> chokika_series_zs())なので)、 $L_n^{(\alpha)}(x) = \begin{pmatrix}n+\alpha\\n\end{pmatrix} \times _1F_1(-n;\alpha+1;s)$
  - さて、検算。上で出した非心カイ分布の確率密度分布から期待値を出して、このLaguerre_polynomialsを使った値とあっていることを。

Laguerre_poly <- function(n,alpha,x,N=100){
	a <- -n
	b <- alpha+1
	tmp <- chokika_series_zs(a,b,x,N)
	tmp <- tmp * exp(lgamma(n+alpha+1)-lgamma(n+1)-lgamma(alpha+1))
	tmp
}

sqrt(pi/2)*Laguerre_poly(1/2,df/2-1,-m^2/2)
sum(g/sum(g) * x)

> sqrt(pi/2)*Laguerre_poly(1/2,df/2-1,-m^2/2)
[1] 4.35449
> sum(g/sum(g) * x)
[1] 4.35449