2011-12-24

指数関数

指数関数は
- $f(t)=k e^{z};z=a+i b$
- $\frac{d f(t)}{dt}=z f(t)$
- $\frac{d^k f(t)}{dt^k}=z^k f(t)$
- $a=0,b=0$ のとき $f(t)=0$
- $a\ne0,b=0$ のとき $f(t)=k e^{at}$ は普通の指数関数(単調増・単調減)
- $a=0,b\ne0$ のとき $f(t)=k e^{ibt}=k(\cos(bt)+i \sin(bt))$ 。この実数部分がこの世で観察可能な部分とすれば $Re(f(t))=k \cos(bt)$ と周期関数(三角関数)
- $a\ne0,b\ne0$ のとき、 $f(t)=k e^{at}\times e^{ibt}$ でこの実数部分は $Re(f(t))=k e^{at}\times \cos(bt)$ と、振幅が単調増または単調減であるような周期関数

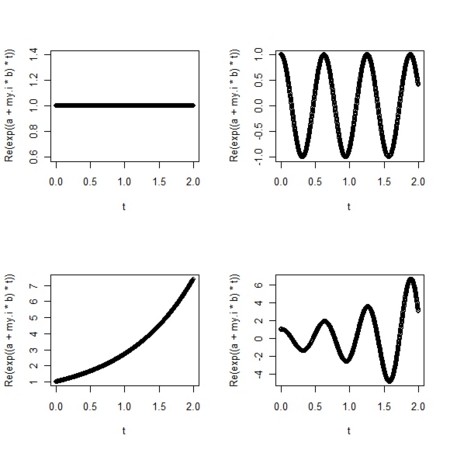
my.i<-complex(real=0,imaginary=1)
my.i
t<-seq(from=0,to=2,length=1000)

par(mfcol=c(2,2))
a<-0;b<-0
plot(t,Re(exp((a+my.i*b)*t)))

a<-1;b<-0
plot(t,Re(exp((a+my.i*b)*t)))

a<-0;b<-10
plot(t,Re(exp((a+my.i*b)*t)))

a<-1;b<-10
plot(t,Re(exp((a+my.i*b)*t)))

$\frac{d^n f(t)}[dt^n}=p f(t)$ となるような微分方程式は $f(t)=k e^{zt};z^n=p$ であるから、任意の $n$ 、任意の実数 $p$ に対して $z^n=p$ となるような複素数 $z$ が取れる( $p>=0$ ならば $z=p^{\frac{1}{n}}$ 、 $p<0$ ならば、 $z=|p|^{\frac{1}{n}}\times (\cos(\frac{2k+1}{n})+i\sin(\frac{2k+1}{n}))$ ただし $k$ は整数)となることがわかる
さて、このように微分方程式的に扱いやすい指数関数(虚数係数を含む)であるが、これの線形和を考えてみる
$g(t)=\sum_{s} r_s e^{z_s t}$ 。ここで $r_s,z_s$ ともに複素数として、観察されるのは $g(t)$ の実数部分 $Re(g(t))$ とする
- ここですべての $s$ について、 $z_s^{n_s} \in \mathbf{R}$ となるような整数 $n_s$ があるときには、 $n_s$ の公倍数 $N_s$ について $\frac{d^{N_s}g(t)}{dt^{N_S}}$ は $r_s$ が実数ならば実数係数だけにしたり、 $r_s\times z_s^{n_s'}$ が実数となるような $n_s'$ についても同様に考えて、複素数の入り乱れを実数係数のみにすることもできそうだ
こんな「複素数係数の指数関数」の「複素数線形和」の関数がどのような形になるかを見てみよう

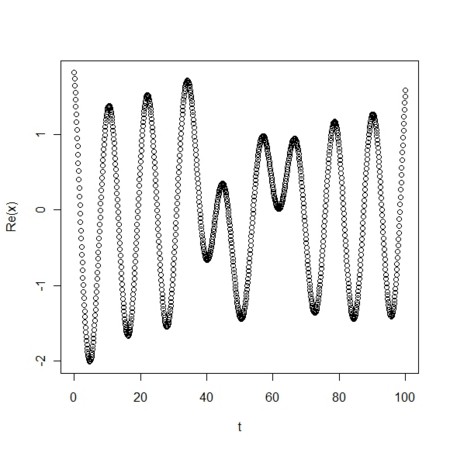
par(mfcol=c(1,1))
t<-seq(from=0,to=100,length=1000)

k<-4
as<-runif(k)
bs<-runif(k)
rs<-runif(k)
ss<-runif(k)
x<-rep(0,length(t))
for(i in 1:k){
	x<-x+(rs[i]+my.i*ss[i])*exp((as[i]*my.i*bs[i])*t)
}

plot(t,Re(x))

要素を複数にしよう
- ２要素が相互に駆け引きをすると、「円」になる
- 複数の要素がすべて相互に駆け引きをすると、ペアワイズに「円」ができる
- その様子

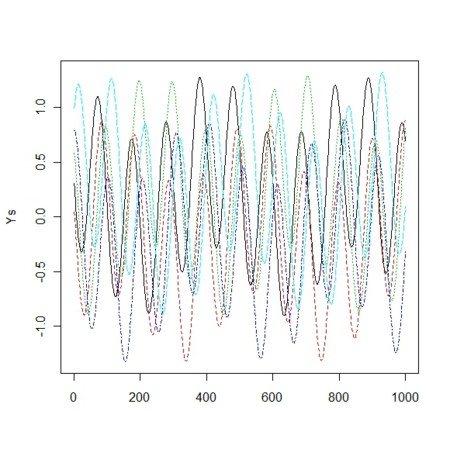
n<-3
#A<-matrix(c(-1,-4,2,5),2,2)

A<-matrix(0,n,n)
A[upper.tri(A)]<-(-1)
A[lower.tri(A)]<-(1)

#A[sample(1:length(A))]<-A
# 固有値分解
eigen.out<-eigen(A)
# P=V,P^{-1}=U
V<-eigen.out[[2]]
U<-solve(V)
B<-diag(eigen.out[[1]])
# xを適当にとって
x<-sort(runif(1000)*10)
# Yの値の格納庫
Ys<-matrix(0,length(x),n)
# 初期値を与え
Ys0<-runif(n)
#Ys0<-c(1,rep(0,n-1))
for(i in 1:(length(x))){
# e^{xB},e^{xA}を計算する
	Bex<-diag(exp(eigen.out[[1]]*x[i]))
	Aex<-V%*%Bex%*%U
# Yの値を計算する
	Ys[i,]<-Aex%*%Ys0
}
# 変化の様子をプロットして
matplot(Ys,type="l")
# ２つの方法が同じ結果であることを確認する
plot(as.data.frame(Ys),cex=0.1)