エルミート、ユニタリ、QR分解、行列の指数関数、行列の対数関数、非可換トーラス、正準交換関係、irrational rotation algebra、不確定性原理

• こちらの記事を読む

library(BosonSampling)
library(complexplus)

m <- 2 # size of matrix (m x m)

U <- randomUnitary(m)
V <- randomUnitary(m)
    
# 複素正方行列
# BosonSampling::randomUnitary() の中身をなぞる
M <- matrix(complex(real = rnorm(m^2), imaginary = rnorm(m^2)),m)
# ユニタリ行列は、複素正方行列のQR分解で得られる

Q <- qr.Q(qr(M))
R <- qr.R(qr(M))
Q
R # 上三角行列
Q %*% R - M # 0

U2 <- Q

round(U2 %*% t(Conj(U2))) # I 

# エルミート行列は複素対角行列

H <- M + t(Conj(M))
# H - t(Conj(H)) = 0
H - t(Conj(H))

# ユニタリ行列はエルミート行列の虚数単位倍の指数関数

U <- matexp(1i * H)
# U %*% t(Conj(U)) = I
round(U %*% t(Conj(U)))
round(t(Conj(U)) %*% U)

# エルミート行列は、ユニタリ行列の対数関数の単位虚数分の１
H2 <- matlog(U) * 1i
# 一般に、matlog(matexp(M)) = M だが
# Mがエルミーと行列の虚数単位倍のときは
# トレースが純虚数になるからなのか(??)
# matlog(matexp(M)) != M となる
H2 - H 
H2 - t(Conj(H2)) # 0



# 量子力学の非可換
# P,Qは物理量を表す作用素（の行列表現）
# PQ - QP = -ih I 
# これを満足する行列 P, Q はない
# これに対してエルミート行列～ユニタリ行列の対応
# P->U, Q-> V
# を考えると
# UV = exp(i \lambda) VU なる関係を持つユニタリ行列 U,Vが存在する
# この式は、exp(i (PQ-QP)) を持ち出して考えればよい
# このU,Vを変数とする、U,V,U^*,V^*の多項式環を考えると
# 非可換環構造が出てくる
# U,Vの例として単純なものが取れるが、それはirrational rotation algebra

• 非可換トーラスは、正方形の紙から辺のペアの貼り合わせによってトーラスを作るが、普通にトーラスを作る貼り合わせではなく、２つの辺ペアのうち１ペアについて、ずらして貼り合わせる。そのずれが無理数のとき、トーラス上の線が閉じずに無限に続く曲線となる。

# トーラスの葉層化
# [0,1] x [0,1]の正方形の紙をトーラスにする
# 普通のトーラスでは、左辺と右辺を貼り合わせ
# 上辺と下辺を貼り合わせる
# 今、左右の辺を貼り合わせたのち
# 上辺の位置 (x,1) と、下辺の位置(x + k,0)を貼り合わせる

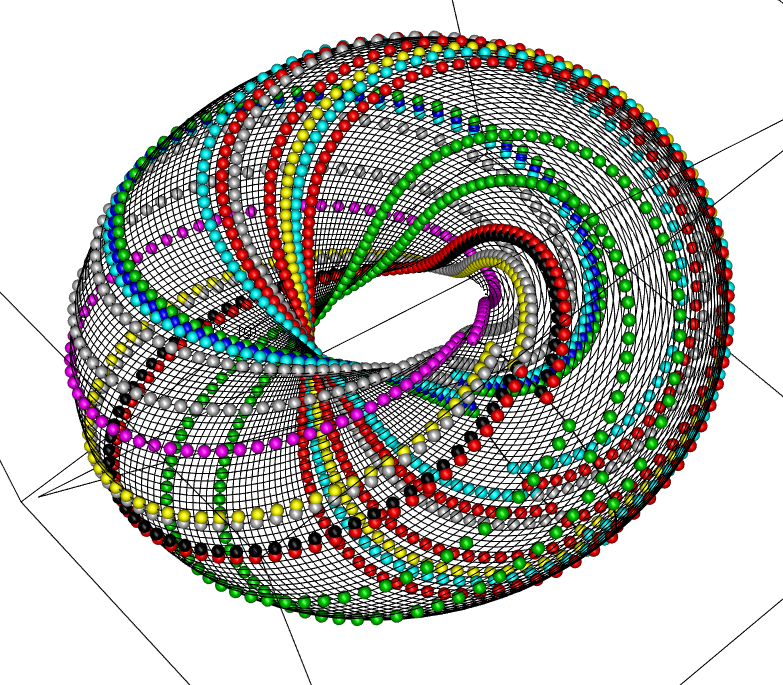
library(rgl)

x <- y <- seq(from=0,to=1,length=100)

xy <- as.matrix(expand.grid(x,y))

R1 <- 3
R2 <- 1.7

X <- R1 * cos(xy[,1] * 2 * pi)
Y <- R1 * sin(xy[,1] * 2 * pi)

k <- 1.04

t <- xy[,2] * xy[,1] + (xy[,2]+k) * (1-xy[,1])

Z <- R2 * cos(t * 2 * pi)
X. <- X + R2 * sin(t * 2 * pi) * cos(xy[,1] * 2 * pi)
Y. <- Y + R2 * sin(t * 2 * pi) * sin(xy[,1] * 2 * pi)

rg <- range(c(Z,X.,Y.))

plot3d(c(X.,rg),c(Y.,rg),c(Z,rg),type="l")

for(i in 1:length(y)){
	r <- runif(1)
	if(r < 0.3){
		s <- which(xy[,2] == y[i])
		spheres3d(X.[s],Y.[s],Z[s],color=i,radius=0.09)
	}
	
}