アダマール・ウォーク

• １次元量子ウォークの中で最もよく研究されているアダマール・ウォーク(こちらを参照)
• Rで実装してみる

# Hadamard walk

U <- 1/sqrt(2) * matrix(c(1,1,1,-1),byrow=TRUE,2,2) + 1i*0

my.PQ <- function(U){
	P <- Q <- matrix(0,2,2)
	P[1,] <- U[1,]
	Q[2,] <- U[2,]
	return(list(P=P,Q=Q))
}


Xinit <- 1/sqrt(2) * c(1,1i)

my.HadamardWalk <- function(U,Xinit,n){
	PQ <- my.PQ(U)
	P <- PQ[[1]]
	Q <- PQ[[2]]
	ret <- list()
	ret[[1]] <- matrix(Xinit,nrow=1)
	
	ret2 <- list()
	ret2[[1]] <- apply(Mod(ret[[1]])^2,1,sum)
	ret3 <- matrix(0,n,n)
	ret3[1,1] <- ret2[[1]]
	for(i in 2:n){
		ret[[i]] <- matrix(0,i,2)
		tmp1 <- matrix(ret[[i-1]][1:(i-1),],ncol=2)
		tmp2 <- matrix(ret[[i-1]][1:(i-1),],ncol=2)
		p <- P %*% t(tmp1)
		q <- Q %*% t(tmp2)
		ret[[i]][1:(i-1),] <- ret[[i]][1:(i-1),] + t(p)
		ret[[i]][2:i,] <- ret[[i]][2:i,] + t(q)
		ret2[[i]] <- apply(Mod(ret[[i]])^2,1,sum)
		ret3[i,1:i] <- ret2[[i]]
	}
	return(list(Q=ret,prob=ret2,probMat=ret3))
}

hout <- my.HadamardWalk(U,Xinit,50)
image(hout[[3]])
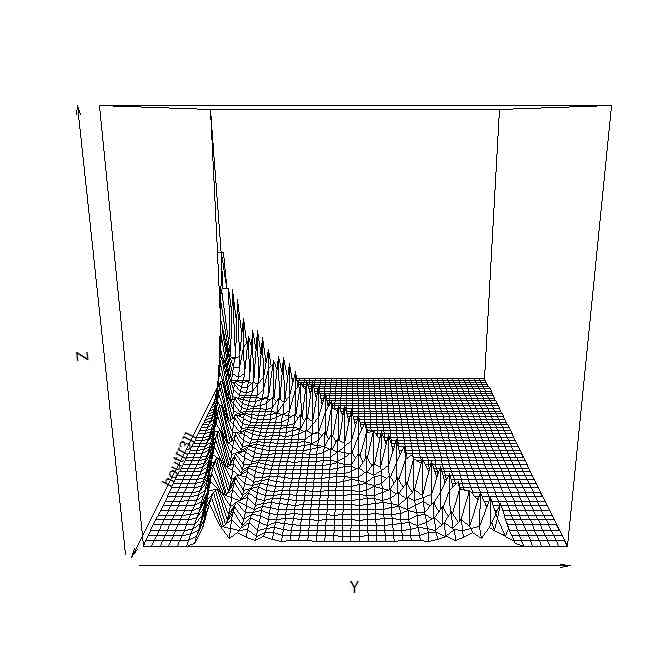
persp(hout[[3]])