球面三角形メッシュ

• 曲面変形を基本形の球から、とすると、いろんな細かさの球面メッシュがほしい。自作する。

my.sphere.tri.mesh <- function(n.psi=30){
	thetas <- list()
	psis <- seq(from=-pi/2,to=pi/2,length=n.psi)
	d.psis <- psis[2]-psis[1]
	hs <- sin(psis)
	rs <- sqrt(1-hs^2)
	ls <- 2*pi*rs
	n.thetas <- floor(ls/d.psis)
	thetas[[1]] <- c(2*pi)
	for(i in 2:(n.psi-1)){
		thetas[[i]] <- seq(from=0,to=2*pi,length=n.thetas[i]+1)
		thetas[[i]] <- thetas[[i]][-(n.thetas[i]+1)]
	}
	thetas[[n.psi]] <- c(2*pi)
	sapply(thetas,length)

	bridge <- list()
	for(i in 1:(n.psi-1)){
		a <- c(thetas[[i]],2*pi)
		b <- c(thetas[[i+1]],2*pi)
		bridge[[i]] <- matrix(c(1,1),1,2)
		loop <- TRUE
		while(loop){
			n.r <- nrow(bridge[[i]])
			id.a <- bridge[[i]][n.r,1] + 1
			id.b <- bridge[[i]][n.r,2] + 1
			if(id.a > length(thetas[[i]]) & id.b > length(thetas[[i+1]])){
				if(id.a-1!=1 & id.b-1!=1){
					bridge[[i]] <- rbind(bridge[[i]],c(1,id.b-1))
				}
				
				loop <- FALSE
			}else{
				if(id.a > length(thetas[[i]])){
					tmp <- c(id.a-1,id.b)
				}else if(id.b > length(thetas[[i+1]])){
					tmp <- c(id.a,id.b-1)
				}else{
					if(a[id.a] < b[id.b]){
						tmp <- c(id.a,id.b-1)
					}else{
						tmp <- c(id.a-1,id.b)
					}
				}
				bridge[[i]] <- rbind(bridge[[i]],tmp)
			}
		}
	}
	xyz <- matrix(0,0,3)
	edge <- matrix(0,0,2)
	triangles <- matrix(0,0,3)
	for(i in 1:n.psi){
		n.r <- nrow(xyz)
		if(i > 1){
			pre <- (n.r-length(thetas[[i-1]])+1):n.r
			post <- (n.r+1):(n.r+length(thetas[[i]]))
			edge <- rbind(edge,cbind(post,c(post[-1],post[1])))
			br <- bridge[[i-1]]
			new.edge <- cbind(pre[br[,1]],post[br[,2]])
			edge <- rbind(edge,new.edge)
			tmp.tri <- cbind(new.edge,rbind(new.edge[-1,],new.edge[1,]))
			tmp <- apply(tmp.tri,1,unique)
			triangles <- rbind(triangles,t(tmp))
		}
		psi <- psis[i]
		theta <- thetas[[i]]
		xyz <- rbind(xyz,cbind(cos(psi) * cos(theta),cos(psi)*sin(theta),sin(psi)))
		
	}
	return(list(xyz=xyz,edge=edge,triangles=triangles))
}
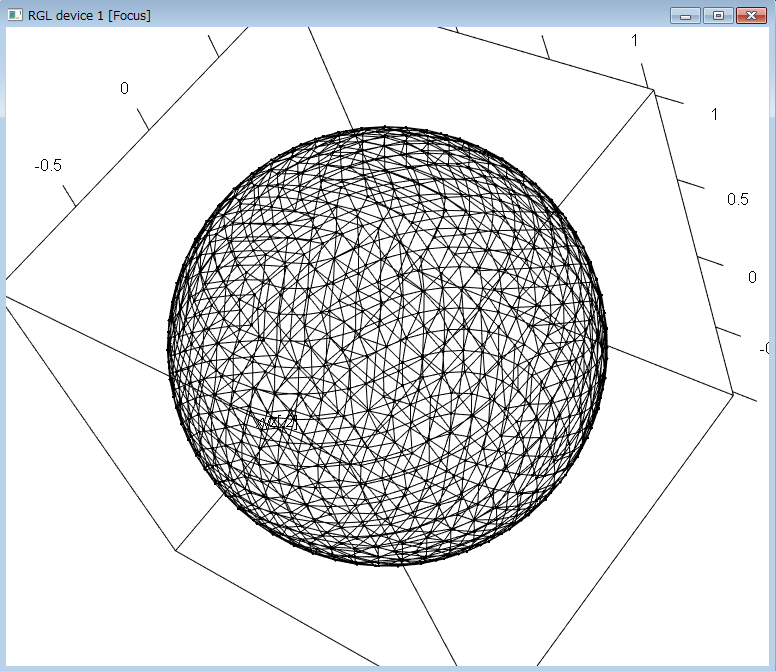
library(rgl)

sp.mesh <- my.sphere.tri.mesh(35)
plot3d(sp.mesh$xyz)
segments3d(sp.mesh$xyz[c(t(sp.mesh$edge)),])

plot3d(sp.mesh$xyz)
mesh.tri <- tmesh3d(t(sp.mesh$xyz),t(sp.mesh$triangles),homogeneous=FALSE)
shade3d(mesh.tri,col="gray")