2014-03-19

二次形式のこと

こちらでGaussian Sequence Modelのことをやっている
$l_p$ ノルムとか二次形式とかがペナルティ関数として出てくる
そこで、二次形式のことを
とてもわかりやすいのはこのページ
- このページからのリンクを併せて読むと、私のようなおじさんが必要な内容はだいたい手に入ります
その上で、自分としての備忘録を以下に
- 二次形式というのは、 $\sum_{i} \sum_{j} a_{ij} x_i x_j$ と表される
- 、のように行列を使っても表せる、ただし、
  - $\alpha_{ii}=a_{ii}$
  - $\alpha_{ij}=\frac{a_{ij}}{2},\text{when } i \ne j$
  - 行列を使って表すと、この行列Aは対象行列。対象行列というのはととのようにの順序を入れ替えたものを同じように扱おうとする行列のこと〜対称・入れ替え可能
    - 以下で、楕円とか双曲線とかの話をするが、そのために一言
      - このように対称行列が出てくるが、対称行列は固有値分解することで、軸報告の拡大・縮小・反転と、回転とに分けることができるので、二次形式を規定している行列も固有値分解して回転と拡大・縮小とに分けることにすれば、ごちゃごちゃした二次の式も $\sum_i a_i x_i^2$ にまとめて議論することができる
- (Cは定数)が描く形が二次形式の幾何学的な意味合いになるのだが、そういう意味で幾何的に言うと、二次形式の２次元版は、楕円・双曲線。そのその「オバケ」が一般次元版
  - 楕円は、円をすべての軸方向に正の値で拡大・縮小したもの
    - 楕円は、円をすべての軸方向に負の値で拡大・縮小してもよい
    - $a x^2 + b y^2 = C$ で表される楕円を考え、xy平面上の点をCの値で色づけをすれば、色のグラデーションで楕円が見える

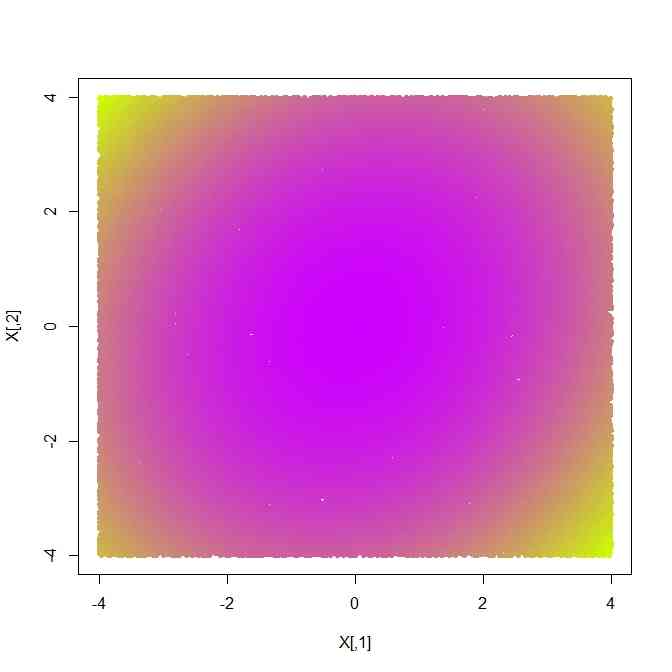
- - 双曲線を同じようにして表すと、 $a x^2 - b y^2 =C$ としたときに、Cの値が正の領域と負の領域がC=0の２直線で仕切られたようなグラデーション図になる

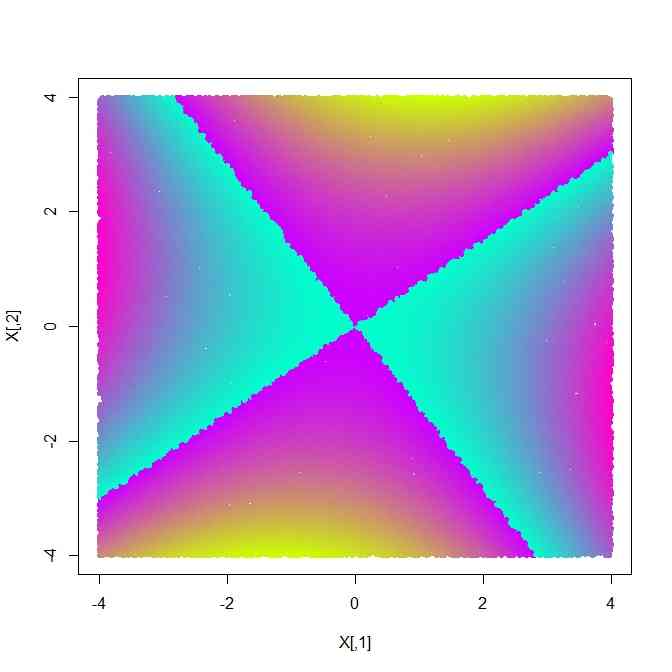
- - 実際、これはどうやって描くか、というと２次元なので2x2行列である対象行列Aを $A=VSV^T$ と固有値分解したときの、２つの固有値(行列Sは固有値を対角成分とする対角行列)の符号を同じにしたのが楕円、正１個、負１個にしたのが双曲線
  - あまり多次元にすると「表示できない」ので３次元にすると
    - ３次元版楕円

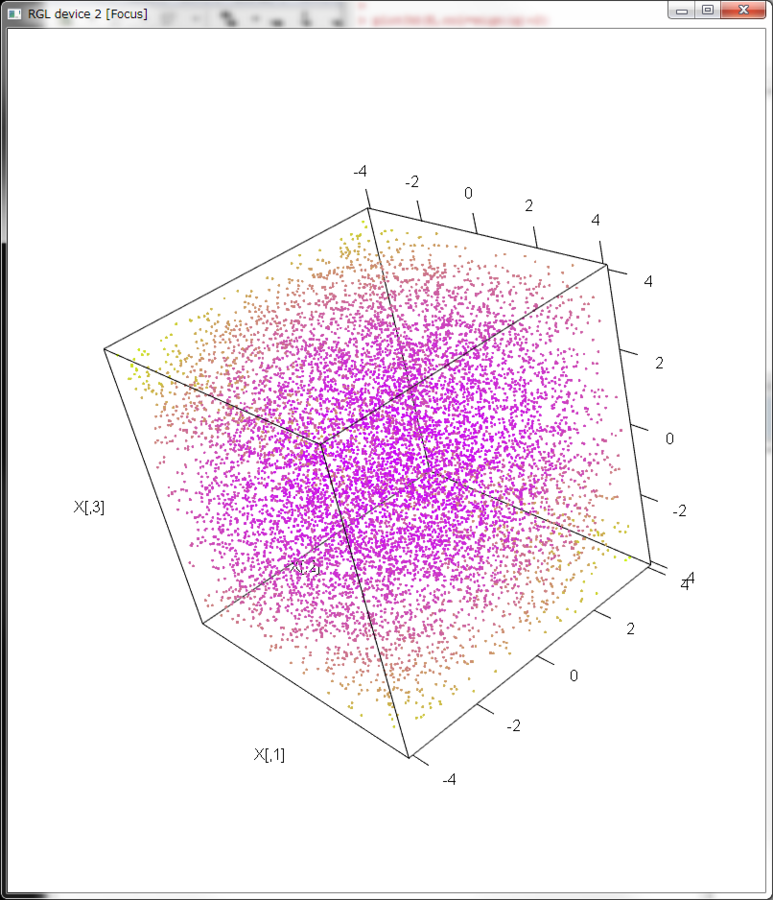
- - - ３次元版双曲線(グラデーションはつけずに、Cの値がの符号で色分けしてある)

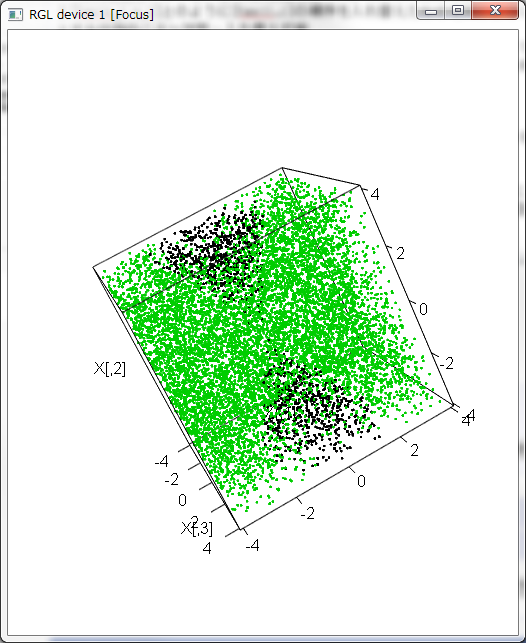
- - - となるが、これも楕円は３個の固有値の符号をそろえてあって、双曲線は１個が正、２個が負(もしくは、１個が負、２個が正)として描く
    - さらに一般化して行くと、「オバケ」になるわけだけれど、固有値の符号が全部そろっていれば、楕円(楕球)、符号が不ぞろいなら、その不ぞろい加減は色々となってくるが、いずれも双曲線オバケ
  - 実際、「楕円とその多次元オバケ」は原点で0となり、そこから遠くなると、のCの符号は変わらず、その絶対値がどんどん大きくなる。だから「楕円様」のグラデーションになる。このことは、のCが0以上か0以下かのいずれかになる、ということを意味する。このようにどんなxを持ってきてもが0以上になるような行列Aを正定値と呼び、逆にどんなxを持ってきても0以下になるようなAを負定値と呼ぶ
    - $x^T A x$ は「距離」としてよい性質を持っている
  - 他方、「双曲線とその多次元オバケ」は、0を取る面があって、xによって正負の両方の値を取る場合で空間が分けられている。Cは正負の両方をとる
以下は、上記のお絵かきのRソース

library(GPArotation)

n <- 3
d <- rnorm(n)
d <- runif(n)
R <- Random.Start(n)
M <- R %*% diag(d) %*% t(R)

eigen.out <- eigen(M)

n.iter <- 10000
q <- rep(0,n.iter)
X <- matrix(0,n.iter,n)
for(i in 1:n.iter){
	x <- runif(n)*sample(c(-1,1),n,replace=TRUE)*4
	X[i,] <- x
	q[i] <- t(x) %*% M %*% x
}
length(which(eigen.out[[1]]<0))
plot(sort(q))


library(rgl)
col <- rep("",n.iter)
col[which(q<0)] <- rgb(abs(q[which(q<0)])/max(abs(q[which(q<0)])),1-abs(q[which(q<0)])/max(abs(q[which(q<0)])),0.8)
col[which(q>=0)] <- rgb(0.8,abs(q[which(q>=0)])/max(abs(q[which(q>=0)])),1-abs(q[which(q>=0)])/max(abs(q[which(q>=0)])))

plot3d(X,col=sign(q)+2)
plot3d(X,col=col)

##########

n <- 2
d <- rnorm(n)
d <- runif(2)
R <- Random.Start(n)
M <- R %*% diag(d) %*% t(R)

eigen.out <- eigen(M)

n.iter <- 100000
q <- rep(0,n.iter)
X <- matrix(0,n.iter,n)
for(i in 1:n.iter){
	x <- runif(n)*sample(c(-1,1),n,replace=TRUE)*4
	X[i,] <- x
	q[i] <- t(x) %*% M %*% x
}
length(which(eigen.out[[1]]<0))
plot(sort(q))


library(rgl)
col <- rep("",n.iter)
col[which(q<0)] <- rgb(abs(q[which(q<0)])/max(abs(q[which(q<0)])),1-abs(q[which(q<0)])/max(abs(q[which(q<0)])),0.8)
col[which(q>=0)] <- rgb(0.8,abs(q[which(q>=0)])/max(abs(q[which(q>=0)])),1-abs(q[which(q>=0)])/max(abs(q[which(q>=0)])))

plot(X,col=col,xlim=range(X),ylim=range(X),pch=20)