超幾何関数 - ryamadaのコンピュータ・数学メモ

昨日の記事で正・非心カイ分布・カイ二乗分布の密度関数の比較をした
比較にあたって、ぎゅっとまとめた関数であるところのベッセル関数、それをさらに一般化した記法で表した超幾何関数を使うと、どこが違うのかはわかりやすかった
超幾何関数についてはこちらがお薦め
今日は、その超幾何関数の式の具合をわかったつもりになるために、Rコード化してべたべたに眺めてみることにする
超幾何級数・関数のWikiはこちら
ポッホハマー記号 $(x)_0 = 1; (x)_n = \prod_{k=0}^{n-1}(x+k)$

pochhammer <- function(x,n){
	if(n==0){
		return(1)
	}else{
		return(prod(x+(0:(n-1))))
	}
}

超幾何級数はベクトルとを引数に
- $_rF_s(\mathbf{a};\mathbf{b};z)=\sum_{n=0}^{\infty} \frac{\prod_{i=1}^r (a_i)_n}{(\prod_{j=1}^s (b_j)_n) n!}z^n$ で表される

# 超幾何級数のn=0,....のうち特定のnについて、特定のzで計算
chokika_single <- function(a,b,z,n){
	a.p <- rep(NA,length(a))
	b.p <- rep(NA,length(b))
	for(i in 1:length(a)){
		a.p[i] <- pochhammer(a[i],n)
	}
	for(i in 1:length(b)){
		b.p[i] <- pochhammer(b[i],n)
	}
	signz <- sign(z)^n
	if(z==0){
		tmp <- 0
	}else{
		tmp <- -lgamma(n+1)+n*log(abs(z))
	}

	if(length(a) > 0){
		tmp <- tmp + sum(log(abs(a.p)))
	}
	if(length(b) > 0){
		tmp <- tmp - sum(log(abs(b.p)))
	}
	return(signz*prod(sign(a.p))*prod(sign(b.p))*exp(tmp))
}

chokika_single(c(1,2),c(3,4),2,3)
# 特定のzについて、n=0,1,....,Nまで足し合わせ(本当はNは無限大)
chokika_series <- function(a,b,z,N = 100){
	ret <- 0
	for(i in 0:N){
		ret <- ret + chokika_single(a,b,z,i)
	}
	ret
}
# さらに複数のzの値のベクトルzsについて計算
# べたべただから、ループだらけで遅いけれども、こうしておけば忘れない
chokika_series_zs <- function(a,b,zs,N=100){
	ret <- rep(NA,length(zs))
	for(i in 1:length(zs)){
		ret[i] <- chokika_series(a,b,zs[i],N)
	}
	ret
}

超幾何関数は、の与え方で色々な関数(初等関数、代数関数、特殊関数など)を同一記法で表せる
- 指数関数: $\mathbf{a}=(),\mathbf{b}=(),z=z$

a <- c()
b <- c()
zs <- seq(from=0,to =10,by=0.01)
y <- chokika_series_zs(a,b,zs)
plot(zs,y)
plot(y,exp(zs))

- $(1-z)^{-a}$ : $\mathbf{a}=(a),\mathbf{b}=(),z=z$

a <- c(2)
b <- c()
zs <- seq(from=-0.5,to =0.5,by=0.01)
y <- chokika_series_zs(a,b,zs)
plot(zs,y)
plot(y,(1-zs)^(-a))

- $log(1+z)$ : $\mathbf{a}=(1,1),\mathbf{b}=(2),z=-z$ と超幾何関数を定め、それの $z$ 倍

zs <- seq(from=-1,to =1,by=0.01)
a <- c(1,1)
b <- c(2)
y <- zs*chokika_series_zs(a,b,-zs)
plot(zs,y)
plot(y,log(1+zs))

$\sin(z)$ : $\mathbf{a}=(),\mathbf{b}=(3/2),z=-z^2/4$ と超幾何関数を定め、それの $z$ 倍

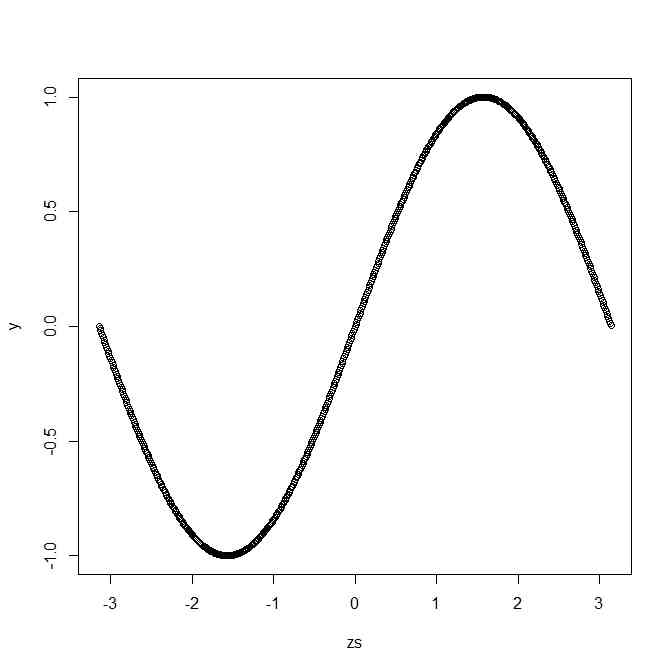
zs <- seq(from=-pi,to =pi,by=0.01)

a <- c()
b <- c(3/2)
y <- zs * chokika_series_zs(a,b,-zs^2/4)
plot(zs,y)