ryamadaのコンピュータ・数学メモ

2012-10-19

n進法とフラクタル

昨日の続き
n進法というのは、整数に関する再帰処理であって、フラクタル的に表すことができる、というのが昨日の話
２進法で $2^k$ の値をフラクタル的に表す別方法を考えてみよう
$2^k$ という値は、k個の要素を持つ集合のべき集合の要素の数（ $\phi,\{1\},\{2\},...,\{k\},\{1,2\},...,\{1,2,...,k\}$
これらの包含順序関係はハッセ図(こちら)で表される
２進法では、このハッセ図を順番にたどって行く作業に他ならない
- (0,0,...,0)->(1,0,...,0)->(0,1,0,...)->(0,0,1,0,...)
このような形式の場合、位が一つ上がるとき(1,10,100,1000というのは、ハッセ図で言うところの、空集合の次の階層の点になることに相当する
そのうえで、その後は、「その点に至るまでの点の動きを再現する」
- たとえば、0->1->10->11 という４点の軌跡があったときに、次には、100になる。そのうえで、100の「上に」0->1->10->11が再現される
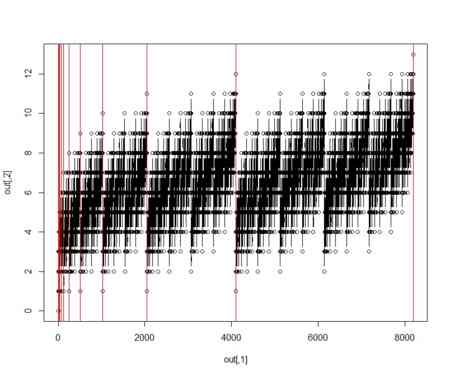
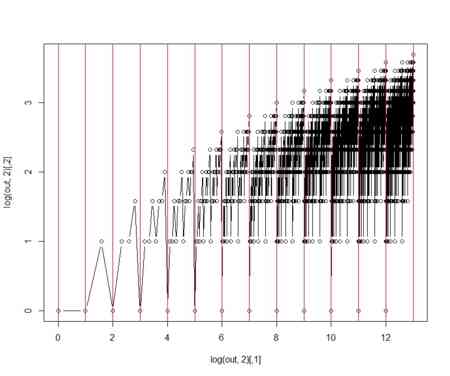
その様子を通常軸と対数軸でプロットしてみよう
- 赤の垂直線は、 $2^k, k=0,1,2,...$ を表す

nishin <- function(n){
	if(n == 0){
		return(matrix(c(0,0),byrow=TRUE,ncol=2))
	}else{
		tmp <- nishin(n-1)
		tail <- tmp[length(tmp[,1]),]
		new.head <- c(tail[1] , 1)
		added <- cbind(tmp[,1] + new.head[1]+1, tmp[,2] + 1)
		return(rbind(tmp,added))
	}
}
k <- 13
out <- nishin(k)
plot(out,type="b")

abline(v = 2^(0:k),col =2)


plot(log(out,2),type="b")

abline(v = log(2^(0:k),2),col =2)