２群に分ける

• こちらで、選択について書いた。選択肢には適切な数があって、その数は、６や７らしい。個人差はあるものの５から９とか
• この５から９とはどういう数なのか
• 今、n.sample個の比較対象があって、それらを「○、×」に分ける指標がn.axis個あるとする
• ○の数が一番多い物がただ一つあったら、決断できると仮定しよう
• そんな「最適」判断が可能な確率は、n.sample数とn.axis数によって決まってくるだろう
• 指標は、最善で、○・×の確率が0.5:0.5であるとしてどんな風になるかを試してみる
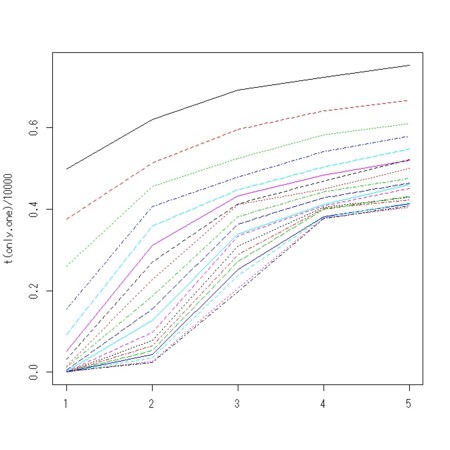
• 確率が５割を超えるのが、n.sample が5−9個あたり、なのかもしれない
• n.sample数が増えると「トップ１」があっても、「セカンドトップ」との得点差が１点だったりする確率が上がるだろうから、「悩ましさ」は増えそうだ。「トップ１」と「セカンドトップ」の得点差が、『何割以上』のときに判断できる、と仮説を変えると、もう少し、n.sample ~ 5...9に峻別力がつくかもしれない

n.iter <- 10000

r <- rep(0,n.iter)


n.samples <- 2:20
n.axiss <- 1:5

only.one <- matrix(0,length(n.samples),length(n.axiss))

for(i in 1:length(n.samples)){
	for(j in 1:length(n.axiss)){
		n.sample <- n.samples[i]
		n.axis <- n.axiss[j]
		for(k in 1:n.iter){
			X <- matrix(sample(c(0,1),n.sample * n.axis ,replace=TRUE),nrow=n.sample)

			sum.x <- apply(X,1,sum)
			r[k] <- length(which(sum.x==max(sum.x)))
		
		}

		only.one[i,j] <- table(r)[1]

	}
}
matplot(t(only.one)/10000,type="l")