2012-09-10

桁を捨てる

R ヒストグラム二進法進法

こちらやこちらで度数分布のことを書いた
１０分割の度数分布とか、１００分割の度数分布とかっていうのは、１０進法表示のうち、上位何桁の違いを有効することにした上で、「同じ値」に扱われるレコードの数を数える、ということ
では、多次元空間で、同様に、適当な「粗さ」でレコード点を格子点に集約することを考える
「格子点」が多すぎるときに、ひとまず、「帰属レコード」がある格子点だけを取り出したいとする
k次元空間にあって、 $10^n$ 分割をk尺度にする場合は、１０進法表示の丸めを使えばよい
$u^n$ 分割をk尺度にする場合に拡張することもできる
準備として次をする

# 0-1の値を扱うことにする
x <- runif(1)
x
# 10進法で
k <- 10
# 小数点以下何桁目まで考慮するかを0,1,2,...,nで決めるとする
n <- 10
floor(x/(k^(0:(-n))))
# ２進法で考えれば…
k <- 2
floor(x/k^(0:(-n)))

> # 0-1の値を扱うことにする
> x <- runif(1)
> x
[1] 0.4840452
> # 10進法で
> k <- 10
> # 小数点以下何桁目まで考慮するかを0,1,2,...,nで決めるとする
> n <- 10
> floor(x/(k^(0:(-n))))
 [1]          0          4         48        484       4840
 [6]      48404     484045    4840452   48404522  484045221
[11] 4840452212
> # ２進法で考えれば…
> k <- 2
> floor(x/k^(0:(-n)))
 [1]   0   0   1   3   7  15  30  61 123 247 495

これを利用してやってみよう
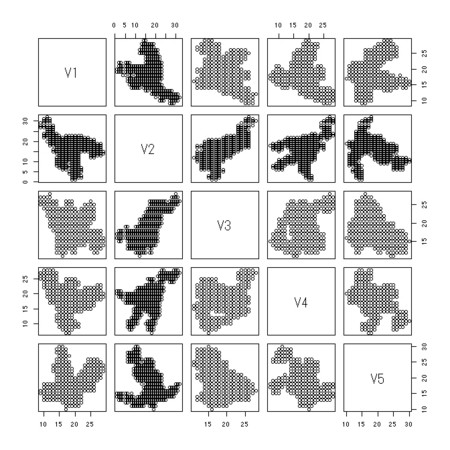
- $(2^5)^10$ 分割すると100万点のほとんどすべてがユニークな点となるようだ
- 図は、偏りが目立つように、次元、10、100本の酔歩道、全点数10万として、各軸 $2^5=32$ 分割して集約したものを、軸１−５に関してペアワイズを取ってプロットしたもの

# 10次元空間に偏りのある100万点を配置する
#データの次元
df <- 10
# 偏った点を作るために、1000本の酔歩道を作って
k <- 1000
# 各道から1000個の点を取る
n.pts <- rep(1000,k)
M <- NULL
for(i in 1:k){
	s <- sample(1:df,n.pts[i],replace=TRUE)
	tmp <- matrix(0, n.pts[i],df)
	for(j in 1:length(s)){
		tmp[j,s[j]]<-sample(c(-1,1),1)
	}
	M <- rbind(M,apply(tmp,2,cumsum))
}
# 長さ１の超立方体に納める
# 道から少し外れさせる
M <- (M-min(M))/(max(M)-min(M))
M <- M + rnorm(length(M)) * 0.01
M <- (M-min(M))/(max(M)-min(M))

plot(M[,1:2])

# k=2進法で細かくする桁を変えてやる
M.list <- list()
unique.M.list <- list()
n.rep <- 5
k <- 2
# 各尺度を k^i に等分する
# したがって、(k^i)^df セルに等分して、点の存在するセルを数え上げていることになる
for(i in 1:n.rep){
	#M.list[[i]] <- round(M,i)
	M.list[[i]] <- floor(M/k^(-i))
	#print(length(which(duplicated(M.list[[i]][,1]))))
	unique.M.list[[i]] <- unique(as.data.frame(M.list[[i]]))
	print("No. total points")
	print(length(M[,1]))
	print("No. unique coordinate points")
	print(length(unique.M.list[[i]][,1]))
}
plot(as.data.frame(M.list[[n.rep]][,1:5]))

# 二進法で１桁目(2^10分割)すると
# 100万点が1025点に集約される
[1] "No. total points"
[1] 1000000
[1] "No. unique coordinate points"
[1] 1025
# 二進法で２桁目((2^2)^10分割)すると
# 100万点が6822点に集約される
[1] "No. total points"
[1] 1000000
[1] "No. unique coordinate points"
[1] 6822
# 二進法で２桁目((2^3)^10分割)すると73499
[1] "No. total points"
[1] 1000000
[1] "No. unique coordinate points"
[1] 73499
# 二進法で２桁目((2^4)^10分割)すると405521
[1] "No. total points"
[1] 1000000
[1] "No. unique coordinate points"
[1] 405521
# 二進法で２桁目((2^5)^10分割)すると913915
[1] "No. total points"
[1] 1000000
[1] "No. unique coordinate points"
[1] 913915