ジャンプのあるブラウン運動

• Levy 過程はこちらにあるように、３つの要素から構成される
  • a Brownian motion
  • a compound Poisson process
  • a square integrable pure jump martingale
• ひとまず、Brownian motionとcompound Poisson processとの和を取ってみる
• Brownian motionはsdeパッケージのsde.sim()関数で、driftの項をなくし、diffusionの項を単純なものとすることで作る
• ついで、ポアッソン過程は、イベントの起きる時刻を指数乱数で発生させ、そのジャンプの距離と向きを一様乱数から発生させたものとする

# Brownian motion
library(sde)
d <- expression(0)
s <- expression(1) 
sde.sim(X0=0,drift=d, sigma=s,N=1000) -> X1
plot(X1,main="Ornstein-Uhlenbeck")

# Compound Poisson process
tmp.t<-rexp(10,2)
jumps<-runif(length(tmp.t),-1,1)

plot(cumsum(tmp.t),jumps,type="l")

X1.v<-c(X1)
X1.t<-seq(from=0,to=max(cumsum(tmp.t)),length=length(X1.v))
diff.X1.v<-diff(X1.v)

X1.v<-X1.v[-1]
X1.t<-X1.t[-1]

X2.v<-jumps
X2.t<-cumsum(tmp.t)

Joint.t<-c(X1.t,X2.t)
tmp.order<-order(Joint.t)

incl<-c(diff.X1.v,X2.v)
incl<-incl[tmp.order]

Joint.X.v<-cumsum(c(0,incl))
Joint.X.t<-c(0,Joint.t[tmp.order])
plot(Joint.X.t)


plot(Joint.X.t,Joint.X.v,type="l")

library(ggplot2)
df<-data.frame(Joint.X.t,Joint.X.v)

gp<-ggplot(data=df,aes(x=Joint.X.t,y=Joint.X.v))
gp.1<-gp +  geom_line()
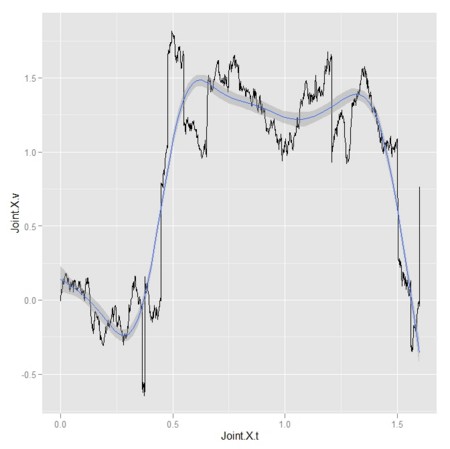
gp.2<-gp.1 + stat_smooth()

#qplot(Joint.X.t,Joint.X.v)

gp.2