相関関数と内積

• ２つの関数関係を表すものに相関関数がある
• 内積の拡張であるという(こちら)
• ２つの有限長のベクトルの内積を、有限長のベクトルの長さの平方根の積で割ると、２つのベクトルのなす角のコサインになる
• 相関関数の場合も、２つの関数の相関関数を、それぞれの関数の自己相関関数(ずれのないときの)の平方根で割ってやれば、関数の「角のコサイン」のようなものが出るはず
• Rでやってみる

# 適当に点をとる
Np<-15
ts<-sort(runif(Np))
vs<-sort(runif(Np))
#vs<-sin((1:Np)/10)
vs<-vs-min(vs)
# 
library(pracma)
# 補間する
# 保管する横軸値として均等配置点を作る
ss<-seq(from=0, to=1,length=1000)
# 観測点の外に外挿入しないために、範囲を狭める
ss<-ss[which(ss>(min(ts)) & ss< max(ts))]
# 保管する
yc<-interp1(ts,vs,ss,method="constant")
yl<-interp1(ts,vs,ss,method="linear")
yn<-interp1(ts,vs,ss,method="nearest")
ys<-interp1(ts,vs,ss,method="spline")
ys<-interp1(ts,vs,ss,method="cubic")
# 補間結果をプロットする
plot(ts,vs)
grid()
lines(ss,yc,col=2)
lines(ss,yl,col=3)
lines(ss,yn,col=4)
lines(ss,ys,col=5)
lines(ss,yc,col=6)

# pracmaパッケージのconvolve()関数を使って、離散数列畳み込みをに基づいて「２関数間のコサイン」を出す関数を作る
my.convolve<-function(x,y,type="open"){
	i.p<-(convolve(x,y,type=type))
	#print(i.p)
	x.x<-max(convolve(x,x,type=type))
	#print(x.x)
	y.y<-max(convolve(y,y,type=type))
	#print(y.y)
	return(list(corr=max(i.p)/sqrt(x.x[1]*y.y[1]),vs=i.p/sqrt(x.x[1]*y.y[1])))
}
# 補間してできた値列同士は、「関数としての相関」が強いはずなので、その値を出しつつ
# 点の付番をパーミュテーションして、「相関」の強さの「珍しさ」を確認してみる
Niter<-1000
ori<-my.convolve(yc,yl)$corr
perm.stat<-rep(0,Niter)
reserve.vs<-vs
for(i in 1:Niter){
	tmpvs<-sample(vs)
	plot(ts,tmpvs)
	tmpyc<-interp1(ts,tmpvs,ss,method="constant")
	lines(ss,tmpyc,col=2)
	lines(ss,yl,col=3)
	perm.stat[i]<-my.convolve(tmpyc,yl)$corr
	if(perm.stat[i]==max(perm.stat,ori)){
		reserve.vs<-tmpvs
	}
}
par(mfcol=c(1,2))
plot(ts,vs)
grid()
tmpyc<-interp1(ts,reserve.vs,ss,method="constant")
lines(ss,tmpyc,col=2)
lines(ss,yl,col=3)
lines(ss,yc,col=4)

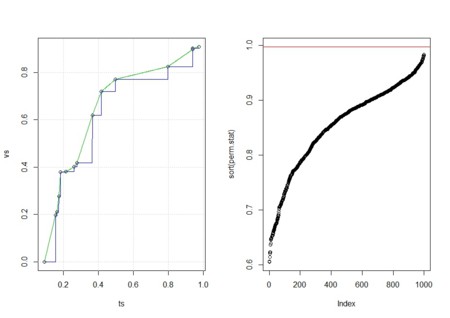
plot(sort(perm.stat),ylim=range(c(ori,perm.stat)))
abline(h=ori,col=2)
par(mfcol=c(1,1))