ryamadaのコンピュータ・数学メモ

2021-11-09

可換環としての団代数

可換環団代数

資料はこちら

https://people.math.harvard.edu/~williams/papers/chapter6.pdf

団代数は、変数があって、変数がクラスタを作って、変異規則によって変異する
変異規則はローラン多項式なので、この変異規則や、変数が満足するべき多項式が決まれば、それは多項式の集まりになっており、環をなす、と、そういう話
クラスタ変数の総数がn、Frozen変数の数がmのとき、n個のクラスタ変数が、ある関係式を満足していると、それはn次元代数多様体になっている
このn変数の代数多様体のイデアルで、n+m変数の多項式環の商を取ると、それが、n+m変数でできた座標環
このn+m変数の座標環に、団代数の変異ルールが付随する
この変異ルールは、n+m変数の座標環を制約しており、n+m変数の環のルールを定めている
冒頭に挙げたPDFの6.1. Introductory examplesの Example 6.1.1 をRで実装してみる
- $Q(x_1,...,x_{2k}) = \sum_{i=1}^k (-1)^{i-1} x_i x_{2k+1-i}$ という方程式を考える
- $Q(x_1,...) = 0$ なる代数多様体。２次超曲面である
- ここで多項式環 $C[x_1,...,x_{2k}]$ の商環 $:C[x_1,...,x_{2k}] / Q(x_1,...,x_{2k})$ を考える。これが（斉次）座標環になっている
- ここで、 $(x_1,x_k,x_{k+1},x_{2k}$ をfrozen variablesとし、これらのほかに、 $k-3$ 個の追加のfrozen variables $p_s = \sum_{i=1}^{s+1} (-1)^{s+1-i} x_i x_{2k+1-i} , s = 1,2,...,k-3$ を追加する
- 残りの $(x_2,...,x_{k-1},x_{k+2},...,x_{2k-1})$ という $(k-2) \times 2$ 個が変化するvariables である
- この団代数に登場する変数はこの $(k-2)\times 2$ 個に尽きる
- この変化するvariablesは、 $k-2$ 個で団をなす
- 団の要素は１つずつ変化するが、その変化は $x_i$ と $x_{2k+1-i}$ とでペアをなし、相互に行ったり来たりするだけの単純な変化を持つことにする
- そうすると、 $(k-2)$ 個の変数がなす団の組み合わせ総数は $(k-2)^2$ 通りできる
- このような変数の変異パターンとして
- $x_i x_{2k+1-i} = p_1 + x_1 x_{2k}; i =2 \text{&} k \ne 3$ , $x_i x_{2k+1-i} =p_{i-1} + p_{i-2}; 3 \le i \le k-2$ , $x_i x_{2k+1-i} =x_k x_{k+1} p_{k-3}; i=k-1$ とすると、上記でうまく行くことが解っている
実際、 $Q(x)=0$ を満足する 2k個の数を与えると、４個のfrozen xとk-3個のprozen pと、k-2個の値を与えることで、残りのk-2個の値は、「変異」演算で復元できるが、これは、2k個の値セットの自由度を2kとしたときに、 $Q(x)=0$ の式の自由度１個分と、4,k-3,k-2の自由度の和が2kになるように、自由度が残っていないことからも説明がつく
別の団代数の例として、2xn行列のn(n-1)/2 個のPlucker座標と、n角形の三角化の話も自由度の点で考えておく
- 2xn行列は成分数が2nあるので自由度が2n。ただし、Plucker座標を考えるときには、その1列を(1,0)に正規化することができる（Plucker座標が相対的な値だから…斉次座標系)。そうすると自由度は2n-2。
- 今、n角形のn本の辺に対応するペアはFrozen
- 三角化すると、n-2本の対角線が引ける
- n + n-2 = 2n -2で、すでにPlucker座標の自由度に達している
- したがって、n角形の辺の値とある三角化のn-2本の対角線の値とを決めると、n(n-1)/2通りあるPlucker座標のすべては決まっている
- 団代数変異が対応して、既知のPlucker座標を１つずつ、変異させ、未知のPlucker座標の値を既知のそれから決めるようなルールがある、というのが、2xn行列のPlucker座標とn角形の三角化にまつわる団代数
- これを「値」ではなく、Plucker座標の算出式とすれば、ローラン多項式環になっているということ（だろう）
このことが、このPDFの6.2のProposition 6.2.1に書かれている。日本語抄訳は以下のようになる
- ランク n の団代数（geometric タイプの団代数で、体をCとする）Aを考える。m-n個のFrozen variablesがある。
- Xを団代数Aの「すべての変数」の集合とする
- Xの要素数は多いが（mより多く、場合によっては無限大（？））、（最初のシードを考えれば、n個の非frozen 変数とm-n個のfrozen 変数とを併せてm個の変数から出発できる。
- ここで、n個の変数 $z_1,...,z_n$ を、すべて、単項関数と見做せば、n個の関数が取れる
- また、m-n個のFrozen変数にも、（制約式のような）関数を対応付ける
- Xのすべての（まだ関数表現を与えていない）変数は、団代数のルールによりm個の関数で構成した関数となる
- このような関数の集まりは、団代数ルールでつながっており、和と積が定義できていて、閉じているという意味で、環
- また、最初のシードの変数に対する単項式関数と（不変な）Frozen関数とが、環全体を張っており、座標環になっている
Example 6.1.1を実装する

my.Q <- function(x){
	n <- length(x)
	tmp <- (-1)^(0:(n/2-1))
	first.x <- x[1:(n/2)]
	second.x <- x[n:(n/2+1)]
	
	ret <- sum(tmp * first.x * second.x)
	return(ret)
}

my.ps <- function(x,s){
	n <- length(x)
	tmp <- (-1)^(s:0)
	first.x <- x[1:(s+1)]
	second.x <- x[n:(n-s)]
	ret <- sum(tmp * first.x * second.x)
	return(ret)
}

my.p.frozen <- function(x){
	n <- length(x)
	n.s <- n/2 -3
	ret <- rep(NA,n.s)
	for(i in 1:n.s){
		ret[i] <- my.ps(x,i)
	}
	return(ret)
}
# n はx.valの数 = 2k
# 変異する変数は 2,3,...,k-1
# i 番目で変異 (2 <= i <= k-1)
# i 番と 2k+1-i 番とが相互に入れ替わる
# 結果として、(k-1)^2の組み合わせができる

my.mutation <- function(v,i,x.frozen,p.frozen){
	n <- length(x.frozen)
	k <- n/2
	new.v <- v
	if(k==3){ # 変異するのはi==2のみ
		new.v[i] <- (x.frozen[k] * x.frozen[k+1] + p.frozen[k-3])/v[i]	
	}else{
		if(i==2){
			new.v[i] <- (p.frozen[1] + x.frozen[1] * x.frozen[2*k])/v[i]
		}else if(i == (k-1)){
			new.v[i] <- (x.frozen[k] * x.frozen[k+1] + p.frozen[k-3])/v[i]
		}else{
			new.v[i] <- (p.frozen[i-1] + p.frozen[i-2])/v[i]
		}
	}
	return(new.v)
}

# 例１
k <- 5
x <- rep(1,2*k)
x[1] <- 0
n <- length(x)
my.Q(x)

p.frozen <- my.p.frozen(x)
x.frozen <- x
x.frozen[c(2:(n/2-1),(n/2+2):(n-1))] <- NA

x.seed <- x[1:(n/2-1)]
x.seed[1] <- NA

v <- x.seed

v.2 <- my.mutation(v,i=2,x.frozen,p.frozen)
v.3 <- my.mutation(v,i=3,x.frozen,p.frozen)
v.4 <- my.mutation(v,i=4,x.frozen,p.frozen)

v.2[2] - x[n-1] # 0 一致する
v.3[3] - x[n-2] # 0 一致する
v.4[4] - x[n-3] # 0 一致する

# 同じi-th 変数での変異は元に戻す
my.mutation(v.2,i=2,x.frozen,p.frozen)
my.mutation(v.3,i=3,x.frozen,p.frozen)
my.mutation(v.4,i=4,x.frozen,p.frozen)


# 例２
k <- 6
#x <- rep(1,2*k)
x <- rep(1:k,2)
n <- length(x)
my.Q(x)

p.frozen <- my.p.frozen(x)
x.frozen <- x
x.frozen[c(2:(n/2-1),(n/2+2):(n-1))] <- NA
n <- length(x)
x.seed <- x[1:(n/2-1)]
x.seed[1] <- NA

v <- x.seed

v.2 <- my.mutation(v,i=2,x.frozen,p.frozen)
v.3 <- my.mutation(v,i=3,x.frozen,p.frozen)
v.4 <- my.mutation(v,i=4,x.frozen,p.frozen)

v.2[2] - x[n-1] # 0 一致する
v.3[3] - x[n-2] # 0 一致する
v.4[4] - x[n-3] # 0 一致する

# 同じi-th 変数での変異は元に戻す

my.mutation(v.2,i=2,x.frozen,p.frozen)
my.mutation(v.3,i=3,x.frozen,p.frozen)
my.mutation(v.4,i=4,x.frozen,p.frozen)

# 例３
k <- 7
#x <- rep(1,2*k)
x <- rep(sample(1:(10*k),k),2)
tmp.Q <- my.Q(x)
n <- length(x)
x[1] <- -(tmp.Q - x[1] * x[n])/x[n]
my.Q(x)

p.frozen <- my.p.frozen(x)
x.frozen <- x
x.frozen[c(2:(n/2-1),(n/2+2):(n-1))] <- NA
n <- length(x)
x.seed <- x[1:(n/2-1)]
x.seed[1] <- NA

v <- x.seed

v.2 <- my.mutation(v,i=2,x.frozen,p.frozen)
v.3 <- my.mutation(v,i=3,x.frozen,p.frozen)
v.4 <- my.mutation(v,i=4,x.frozen,p.frozen)

v.2[2] - x[n-1] # 0 一致する
v.3[3] - x[n-2] # 0 一致する
v.4[4] - x[n-3] # 0 一致する

# 同じi-th 変数での変異は元に戻す
my.mutation(v.2,i=2,x.frozen,p.frozen)
my.mutation(v.3,i=3,x.frozen,p.frozen)
my.mutation(v.4,i=4,x.frozen,p.frozen)

# 例４
k <- 8
#x <- rep(1,2*k)
x <- rep(sample(1:(10*k),k)+sample(1:(10*k),k) * 1i,2)
n <- length(x)
my.Q(x)

p.frozen <- my.p.frozen(x)
x.frozen <- x
x.frozen[c(2:(n/2-1),(n/2+2):(n-1))] <- NA
n <- length(x)
x.seed <- x[1:(n/2-1)]
x.seed[1] <- NA

v <- x.seed

v.2 <- my.mutation(v,i=2,x.frozen,p.frozen)
v.3 <- my.mutation(v,i=3,x.frozen,p.frozen)
v.4 <- my.mutation(v,i=4,x.frozen,p.frozen)

v.2[2] - x[n-1] # 0 一致する
v.3[3] - x[n-2] # 0 一致する
v.4[4] - x[n-3] # 0 一致する

# 同じi-th 変数での変異は元に戻す
my.mutation(v.2,i=2,x.frozen,p.frozen)
my.mutation(v.3,i=3,x.frozen,p.frozen)
my.mutation(v.4,i=4,x.frozen,p.frozen)

2021-11-08

アフィンスキーム、可換環、代数幾何

アフィンスキーム可換環代数幾何

こちらのブログの３記事でアフィンスキームが書かれている(第１

tsujimotter.hatenablog.com
、第２
tsujimotter.hatenablog.com
、第３
tsujimotter.hatenablog.com
)

代数幾何では、多項式の零点集合を考えて、それを多様体～空間として考えることで代数「幾何」になっている
多項式には色々な表現があるが、それを一意性を持って議論するための道具立てがイデアルとかラジカル・イデアルとかになる。ラジカル・イデアルと素イデアル(プライム・イデアル)とはどちらも「構成素として大事な」もの…(こちら

math.stackexchange.com
)

代数多様体が多項式の世界(多項式環)で定まっているけれど、それの双対(のようなもの。。。多分、双対そのもの)として、座標環というものが取れるらしい
この座標環は、多項式全体をイデアルで同一視したもの(商環？）に相当する
多項式環では、多項式を「数」と見ているから、その加減乗除を考えるし、ある多項式で割って割り切れるかどうかを考えることは、もちろん自然なこと
代数多様体は「多項式のセットが定めた」「点の集合」だったが、座標環の方は、「関数の集合」になっている
この座標環も環だから、一意性を持って議論するには道具立てが必要で、素イデアルを考えたい。この素イデアルのことをスペクトルと言う(らしい)
素イデアルの「素」は素数の「素」だが、それは、イデアルで割って割り切れるかどうかという話とつながっている
このスペクトルには、包含関係(のようなもの）があるから、位相が定められる(この位相をザリスキ位相と言う)
位相があるので、座標環の世界にも「幾何」的なものがあることになる
ここに来て、多項式環から始まって、その座標環側に幾何対象が現れたが、これが、「可換環の幾何」
座標環が多項式の零点集合に対して「双対」になっていると書いた
これは、抽象ベクトル空間において、その空間をスカラー空間に線形写像するとき、線型汎関数の空間を考えることができて、それが双対空間だ、という話と対応する話だから
と、いうわけで、可換な多項式環と代数幾何とその双対空間的な者の幾何のぼんやりとした話が見えてきたわけだが、この多項式環の方に非可換なものを考えるとき、同様に、双対空間のようなものと、それのスペクトルが作る位相空間を扱うことにすれば、それが非可換幾何ということなのだろう

2021-11-05

正準交換関係にある２つの行列の無限次元版

正準交換関係行列の指数関数行列の対数関数非可換トーラス置換行列

昨日の記事

Wyle form, 正準交換関係, 非可換トーラス - ryamadaのコンピュータ・数学メモ
で、非可換トーラス絡みのことを書いた

非可換トーラスを具体的に想定するときに、clock and shift matricesというのが使える、と言う話も書いた
そのことは、量子力学における二つの物理量に対応する作用素行列が非可換であること( $PQ - QP \ne 0 I$ )と関係があるが、有限次元作用素行列では、このようなPQの実現ができないことも書いた
その代わり、作用素行列がエルミート行列Hであるとき $U = exp(2 \pi i H)$ という対応を取れば、 $PQ-QP \ne =0 I$ は $UV = i t VU$ に対応するというWyle formがあるという話もした
このU,Vはclock and shift 行列として実現できて、有限次元正方行列表現が与えられるのだった
この有限次元clock and shift 行列の対数関数を取ることで、P,Qを作れる。有限次元のままだと、 $PQ - QP \ne 0 I$ は実現できないが、clock and shift行列の次元を上げていくと、どういう行列ができるのか、それの対数関数を取ると、どういうことになるのか、は計算機実験できるだろう
ということでやってみる
clock行列というのは、対角行列であって、対角成分が、 $exp(2\pi k/d) ; k = 0,1,2,...,d$ なる行列である
これの対数関数は、単純に対角成分の対数を取るだけなので、対角成分が $0,2\pi 1/d, 2\pi \times 2 /d, ..., 2 \pi \times (d-1)/d$ というような行列である。これの無限次元極限は、対角成分が、0から $2\pi$ まで等間隔で増えるような関数 $2 \pi t; 0 \le t < 1$ である
他方、shift 行列は、オフダイアゴナル成分が１で、１か所だけ、右上隅に１が立つような行列である。これの対数関数は次のような性質を持つ
対角成分は0
１行目は、0に引き続いて、大きく負になり、次に、正に転じて、また負、というように正負の値を交互に取る。最後の値は、２番目の値(負の値)の絶対値になる
この１行目の値のシリーズの振動は、両端の絶対値が大きく、中央は０に近い
行列全体としては、この１行目の値のシリーズを一列ずつずらした形となるので、オフダイアゴナルの値は一定、オフオフダイアゴナルの値も一定、というような行列で、歪対称になる
無限大に飛ばすと、最初の成分は０で、２番目と最後の値がある値を取って、符号が逆。それ以外の値は０に収束する方向で変化していくが、さらなる極限を考えると次のようになる
１行目の２番目と最後の値とは、他の行では対角成分をサンドイッチする成分に対応するが、その値が符号違いで大きさのある値になり、対角成分をゼロに「切り違う」。このことを極限に突き詰めると、サンドイッチ成分も結局は０に収束し、対角成分に「切り違い」に相当する値が現れることに相当します。それは、実数で考えるとゼロだが、何か隠れた値である、と言うことになります
結局、対角成分が純虚数であるような対角行列と言うことになるのでしょう。しかも、すべての対角成分は同じ純虚数。ただし、やはり切り違っている関係上、対角成分の値には、左側から作用するときと右側から作用するときとで、正負が異なるような不思議なものになるようです。
このようにすると、clock行列の対数関数は、対角成分が $2 \pi i t; 0 \le t <1$ なので、それを使って対応するエルミート行列を取れば、対角線に $f(x) = x; 0 \le x < 1$ なる関数が立っている無限次元対角行列
また、shift 行列の対数関数は、対角成分がある純虚数でそろっている対角行列となり、それに対応するエルミート行列は、単位行列の定数倍に見える行列。ただし、右からかけた場合と左からかけた場合で対角成分の符号が異なる、というような行列
PQとQPとはどちらも対角成分２個の積になるけれど、片方の対角行列が右作用・左作用で符号が変わるため、PQとQPの符号が違うため、PQ-QPは０にならない、と。そんな感じのようだ
ただし、このままだと、 $PQ - QP = k I$ というように、単位行列の定数倍にならない。どこかに何かの工夫が要るのかもしれない・・・。clock行列の対角成分は足して０(トレースが0)だが、これを、次元乗すると、単位行列になることはなる・・・。したがって、右辺は $kI$ になる、というより、Iは単位行列ではなくてIの●乗根行列と言うことなのかもしれない・・・

d <- 100

w <- exp(2*pi*1i*(0:(d-1))/d)

P <- diag(w)

P. <- matlog(P)

plot(Im(diag(P.)))

d <- 3

Q3 <- diag(rep(1,d))
Q3 <- Q3[,c(2:d,1)]


Q.3 <- matlog(Q3)
plot(Q.3[1,])

d <- 5

Q5 <- diag(rep(1,d))
Q5 <- Q5[,c(2:d,1)]


Q.5 <- matlog(Q5)
plot(Q.5[1,])



d <- 7

Q7 <- diag(rep(1,d))
Q7 <- Q7[,c(2:d,1)]

A <- Q7
Q.7 <- matlog(Q7)
plot(Q.7[1,])

d <- 9

Q9 <- diag(rep(1,d))
Q9 <- Q9[,c(2:d,1)]


Q.9 <- matlog(Q9)
plot(Q.9[1,])

d <- 101

Q11 <- diag(rep(1,d))
Q11 <- Q11[,c(2:d,1)]


Q.11 <- matlog(Q11)
plot(Q.11[1,])


image(Q.11)

2021-11-04

Wyle form, 正準交換関係, 非可換トーラス

正準交換関係 Wyle form 非可換トーラス

量子力学では、物理量が作用素
二つの作用素P,Qがあったとき、非可換なこともあり $PQ-QP = a\times I \ne 0$ 。
これと二つの物理量を同時に測定できないこととかが関係する
他方、このような非可換作用の幾何の例として非可換トーラスと言うものがある
非可換トーラスは、正方形の紙の左右の辺を普通に貼り合わせ、その紙の上下の辺をずらして張り合わせることで作る、という話がある
この２つの話をつなぐときに出てくるのがWyle form(Wiki 記事)
今、非可換作用素P,Qは有限次元正方行列では実現できないことが知られている。その証明としてあちこちで見つけられるのは $tr(PQ-QP) = tr(PQ) - tr(QP) = 0$ だが、 $tr(a \times I) \ne 0$ という話。要するに、作用素P,Qには(正方)行列表現があってほしいが、有限サイズの行列では不可能、ということ。言い換えると、非可換な物理量を考えるとき、無限サイズを考えなくてはならない、と言う話
無限サイズの行列を考えればよいのであれば、数学的にはそうすればよいだけのことだけれど、無限が想像しにくい人にとってはつらいので、少し、判りやすく、有限次元行列で、それっぽさを表せないか、というのが、Wyle form(理解力の乏しい人のために出てきたものではないのだろうが、結果として、その役に立つ)
今、量子力学での作用素に対応する行列P,Qはエルミート行列である(らしい)
エルミート行列には、もれなくユニタリ行列が対応していて $U = exp(i \times P)$ というような関係がある
今、エルミート(無限次元)行列P,Qが $PQ - QP = -ih$ のとき、 $U_s = exp(is P), V_t = exp(it Q)$ というようなユニタリ行列が、(実)パラメタs,tを使って対応付けられて、 $U_s V_t = exp(-ihst) V_t U_s$ となると言う
P,Qは無限次元なので、それに対応するU,Vも無限には作れないので、この式が成り立つと言われても、たいして理解が進むわけではない。
。。。が、よくある説明は、この $U_s$ はある関数fに作用して、 $f(x) \to f(x-hs)$ と定数シフトをする作用素であり、 $V_t$ は関数fに作用して $f(x) \to exp(itx) f(x)$ のように値を倍する作用素である、との説明がなされる
このようにU,Vの作用の「意味」が解って来ると、本来、U,Vは無限次元行列だが、その有限版を作ることは思いつく
定数シフトUとはどういうことかというと、世界を離散的に区切ってやれば、そして、世界が閉じていれば、対角成分が０で第一オフダイアゴナル成分が１で、かどっこにもう一つ１が立っているような置換行列を代表例として取ることができる
また、値を複素数倍する行列Vは、対角行列であって、その対角成分が、１のn乗根であるようなそれを想定することができる
この２種類の行列は the clock and shift matrices と呼ばれる(こちら)
そうしたときに、UVとVUの関係は、1のn乗根倍という関係で繋がっていることを有限行列で示すことは容易である
Rでやってみる

library(complexplus)

d <- 3

# 1のd乗根
w <- exp(2 * pi * 1i /d)
w^d # 1

wd <- w^(0:(d-1))

# Uは置換行列
U <- diag(rep(1,d))
U <- U[,c(2:d,1)]
U
# Vは(x-1)^d=0の根を対角成分とする対角行列
V <- diag(wd)
V

UV <- U %*% V
VU <- V %*% U

k <- w

round(k * UV - VU) # 0

# U,Vからその対数関数をとって、有限次元版 P, Qを作っても、PQ -QP=a Iとはならない
P <- matlog(U) * 1i
Q <- matlog(V) * 1i

P
Q

P %*% Q - Q %*% P

> U
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    1    0    0
[3,]    0    1    0
> # Vは(x-1)^d=0の根を対角成分とする対角行列
> V
     [,1]            [,2]            [,3]
[1,] 1+0i  0.0+0.0000000i  0.0+0.0000000i
[2,] 0+0i -0.5+0.8660254i  0.0+0.0000000i
[3,] 0+0i  0.0+0.0000000i -0.5-0.8660254i

> round(k * UV - VU) # 0
     [,1] [,2] [,3]
[1,] 0+0i 0+0i 0+0i
[2,] 0+0i 0+0i 0+0i
[3,] 0+0i 0+0i 0+0i

2021-11-02

エルミート、ユニタリ、QR分解、行列の指数関数、行列の対数関数、非可換トーラス、正準交換関係、irrational rotation algebra、不確定性原理

R BosonSampling エルミート行列ユニタリ行列行列の指数関数行列の対数関数 QR分解 irrational rotation algebra 正準交換関係不確定性原理

こちらの記事を読む

library(BosonSampling)
library(complexplus)

m <- 2 # size of matrix (m x m)

U <- randomUnitary(m)
V <- randomUnitary(m)
    
# 複素正方行列
# BosonSampling::randomUnitary() の中身をなぞる
M <- matrix(complex(real = rnorm(m^2), imaginary = rnorm(m^2)),m)
# ユニタリ行列は、複素正方行列のQR分解で得られる

Q <- qr.Q(qr(M))
R <- qr.R(qr(M))
Q
R # 上三角行列
Q %*% R - M # 0

U2 <- Q

round(U2 %*% t(Conj(U2))) # I 

# エルミート行列は複素対角行列

H <- M + t(Conj(M))
# H - t(Conj(H)) = 0
H - t(Conj(H))

# ユニタリ行列はエルミート行列の虚数単位倍の指数関数

U <- matexp(1i * H)
# U %*% t(Conj(U)) = I
round(U %*% t(Conj(U)))
round(t(Conj(U)) %*% U)

# エルミート行列は、ユニタリ行列の対数関数の単位虚数分の１
H2 <- matlog(U) * 1i
# 一般に、matlog(matexp(M)) = M だが
# Mがエルミーと行列の虚数単位倍のときは
# トレースが純虚数になるからなのか(??)
# matlog(matexp(M)) != M となる
H2 - H 
H2 - t(Conj(H2)) # 0



# 量子力学の非可換
# P,Qは物理量を表す作用素（の行列表現）
# PQ - QP = -ih I 
# これを満足する行列 P, Q はない
# これに対してエルミート行列～ユニタリ行列の対応
# P->U, Q-> V
# を考えると
# UV = exp(i \lambda) VU なる関係を持つユニタリ行列 U,Vが存在する
# この式は、exp(i (PQ-QP)) を持ち出して考えればよい
# このU,Vを変数とする、U,V,U^*,V^*の多項式環を考えると
# 非可換環構造が出てくる
# U,Vの例として単純なものが取れるが、それはirrational rotation algebra

非可換トーラスは、正方形の紙から辺のペアの貼り合わせによってトーラスを作るが、普通にトーラスを作る貼り合わせではなく、２つの辺ペアのうち１ペアについて、ずらして貼り合わせる。そのずれが無理数のとき、トーラス上の線が閉じずに無限に続く曲線となる。

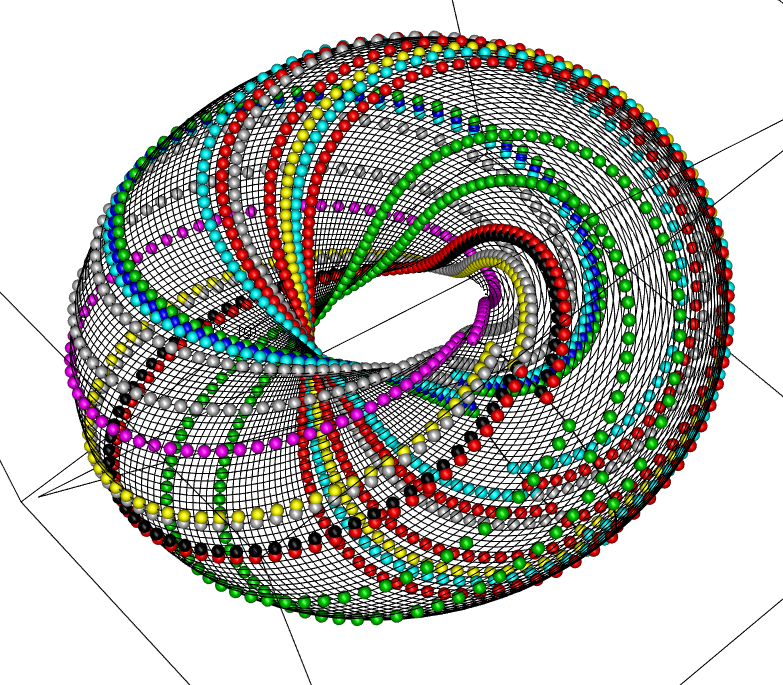
f:id:ryamada:20211102131035p:plain

# トーラスの葉層化
# [0,1] x [0,1]の正方形の紙をトーラスにする
# 普通のトーラスでは、左辺と右辺を貼り合わせ
# 上辺と下辺を貼り合わせる
# 今、左右の辺を貼り合わせたのち
# 上辺の位置 (x,1) と、下辺の位置(x + k,0)を貼り合わせる

library(rgl)

x <- y <- seq(from=0,to=1,length=100)

xy <- as.matrix(expand.grid(x,y))

R1 <- 3
R2 <- 1.7

X <- R1 * cos(xy[,1] * 2 * pi)
Y <- R1 * sin(xy[,1] * 2 * pi)

k <- 1.04

t <- xy[,2] * xy[,1] + (xy[,2]+k) * (1-xy[,1])

Z <- R2 * cos(t * 2 * pi)
X. <- X + R2 * sin(t * 2 * pi) * cos(xy[,1] * 2 * pi)
Y. <- Y + R2 * sin(t * 2 * pi) * sin(xy[,1] * 2 * pi)

rg <- range(c(Z,X.,Y.))

plot3d(c(X.,rg),c(Y.,rg),c(Z,rg),type="l")

for(i in 1:length(y)){
	r <- runif(1)
	if(r < 0.3){
		s <- which(xy[,2] == y[i])
		spheres3d(X.[s],Y.[s],Z[s],color=i,radius=0.09)
	}
	
}

2021-10-30

パラパラめくる『ヒルベルト空間と線形作用素』

パラパラめくるシリーズヒルベルト空間線形作用素

ヒルベルト空間と線型作用素 [ 日合　文雄 ]

価格: 3740 円
楽天で詳細を見る

第１章　ヒルベルト空間
- ノルムが定まっているのがノルム空間
- ノルム空間で会って、距離が完備なのが、バナッハ空間
- さらに内積が定まっているのが、前ヒルベルト空間。内積が定まり、かつ、距離が完備だとヒルベルト空間
  - 内積を考えるとき、実ベクトルの内積は、 $\sum_{i=1}^n a_i^2$ だが、複素ベクトルの内積は $\sum_{i=1}^n a_i \overline{a_i}$ と複素共役が出てくる。このため、 $(x,y)= \overline{(y,x)}$ とか、そういう計算になる
  - 内積の正定値性と共役複素数が出てきて定まる性質とに対して「双線形性」と言う名前がついており、内積は、「値」を返すので「関数」としての性質も持つから、「内積は双線形汎関数」であるという

>library(complexplus)
> u <- c(1+1i*2,2+1i*1)
> u * Conj(u)
> v <- c(2-1i*1,3+3*1i)
> u * Conj(v)
> v * Conj(u)
> u * v
> um <- matrix(u,ncol=1)
> vm <- matrix(v,ncol=1)
> t(Conj(vm)) %*% um
     [,1]
[1,] 9+2i
> t(Conj(um)) %*% vm
     [,1]
[1,] 9-2i
> t(Conj(um)) %*% um
      [,1]
[1,] 10+0i

library(complexplus)

n <- 2
u <- runif(n) + 1i * runif(n)
v <- runif(n) + 1i * runif(n)

# innner product of complex vectors

my.ip.complex <- function(u,v){
	Conj(t(matrix(u,ncol=1))) %*% matrix(v,ncol=1)
}

uv <- my.ip.complex(u,v)
vu <- my.ip.complex(v,u)

uv - Conj(vu) # 0


alpha <- runif(1) + 1i * runif(1)

u.alphav <- my.ip.complex(u,alpha * v)
alphau.v <- my.ip.complex(alpha * u,v)

u.alphav
alphau.v

alpha * uv
alpha * vu

u.alphav - alpha*uv # 0
alphau.v - Conj(alpha*vu) # 0


my.ip.complex(alpha * u, v) - my.ip.complex(u,Conj(alpha) * v) # 0
my.ip.complex(alpha * u, v) - Conj(alpha*vu) # 0
my.ip.complex(u,Conj(alpha) * v) - Conj(alpha) * uv # 0
my.ip.complex(alpha * u, v) - Conj(alpha) * uv # 0

- 線形作用素。有界なものを対象にすることにする。線形作用素は、ノルム空間Xからノルム空間Yへの写像が線形であるとき、それは線形作用素。Yが体Kのときは、線型汎関数。線形汎関数全体の集合を双対空間(または共役空間)と言う
- バナッハ空間と商バナッハ空間。商バナッハ空間のノルムは商ノルム
- 再生核ヒルベルト空間は、複素関数からなる空間で、複素関数の返す複素数が連続であるようなもの
第２章　ヒルベルト空間上の線形作用素
- 有限次元で考えれば、ヒルベルト空間上の線形作用素は行列で表現される。無限次元のそれは無限次元行列で表現されることになる
- ヒルベルト空間上の有界作用素には
  - 自己共役作用素、正規作用素、等距離作用素、ユニタリー作用素、射影作用素などがある
- 複素内積では $(x,y)= \overline{(y,x)}$ から $(\alpha x, y) = (x,\overline{\alpha}y)$ だが、この複素数 $\alpha$ を作用素と見れば、これと同じような働き方をする作用素 $A$ は、その共役作用素 $A^*$ を持って、 $(x,Ay) = (x, A^* y)$ というような作用素が自然に認められる。これが共役作用素

my.ip.complex(alpha * u, v) - my.ip.complex(u,Conj(alpha) * v) # 0

- $A = A^*$ のとき、Aは自己共役(エルミート)
- $A^*A = A^*A$ のとき、Aは正規
- $A^*A= AA^* = I$ のとき、Aはユニタリ―作用素
- $\forall x, (Ax,x) \ge 0$ のとき、Aは正定値
- $P^* = P = P^2$ のとき、自己共役かつ冪等であるわけだが、これを射影作用素と言う
- 非線形作用素もある
第３章　スペクトル分解
- 行列の固有値の概念を拡張して、作用素のスペクトルを考える
- 有限行列は固有値と対応する射影行列との積の和に分解できる。作用素は無限次元版なので、固有値相当の値と射影作用素との積の積分になる
第４章　ヒルベルト空間上のコンパクト作用素
- コンパクト作用素は有限次元の行列を位相的な意味で直接に一般化したもの
第５章　作用素単調関数と作用素平均
- 作用素の代数的な構造を考えたり、ノルム構造や位相的な性質に着目して考えることがある。複素解析定な方法もある。作用素の順序関係を考えることもある(ここでの順序とは、正定値性から定まる自己共役作用素の間の順序のこと)
- 順序があれば単調関数のようなものが考えられる。作用素平均は順序を保つ正定値作用素間の二項演算。電気回路の直列・並列などと関係がある
第６章　特論
- $\forall x, ||Ax|| = ||x||$ のとき、Aは等距離作用素

2021-10-28

非可換トーラスのメモ

非可換幾何作用素環非可換トーラス