- 卵や栗の形を3次元空間にある閉じた2次元多様体とみる
- この3次元空間にある2次元多様体を、4次元空間にある2次元多様体の射影3次元空間への像とみる
- 4次元空間にある2次元多様体を4次元空間にある1次元多様体であるところのらせんをある回転軸についてぐるりと回してできる「円筒」とみる
- 4次元空間のらせんを「2次元分の指数曲線」と「2次元の円周繰り返し」との組み合わせとして作る
d <- 0.9
lambdas <- c(d,-1,0+q*1i,0-q*1i )
V <- matrix(c(1,0,0,0,0,1,0,0,0,0,1,-1i*1,0,0,1,1i*1),4,4)
x.init <- rep(1,4)
t <- seq(from=-3,to=3,length=100)
X <- matrix(0,length(t),4)
for(i in 1:4){
X[,i] <- x.init[i] * exp(lambdas[i]*t)
}
X. <- Re(t(V%*% t(X)))
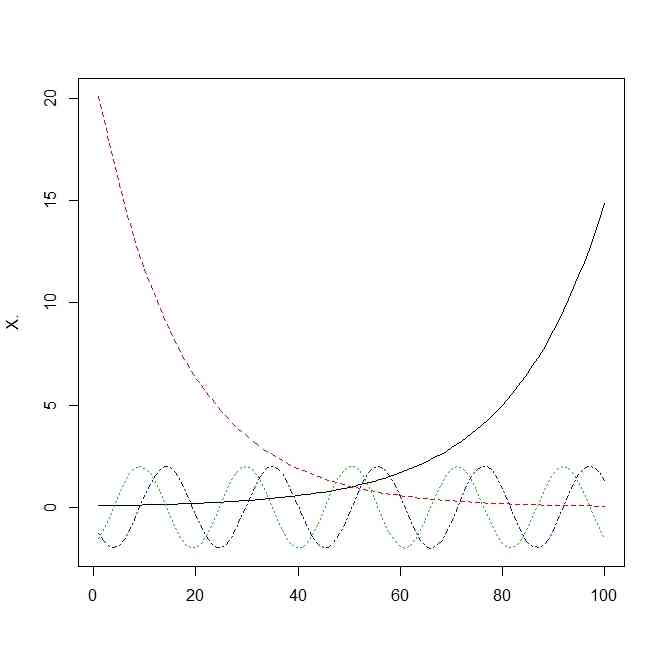
matplot(X.,type="l")
- 3次元射影空間の像を作る
- この射影によって、らせんの両端の無限遠点を特定の2点(1,0,0),(-1,0,0)へと写す
- この射影によって、周回成分の2次元はらせんの進行軸の拡縮に応じた拡縮変化以外は受けないようにする
- これを実現するのが、次の変換行列
- 射影前の座標の様子はこう
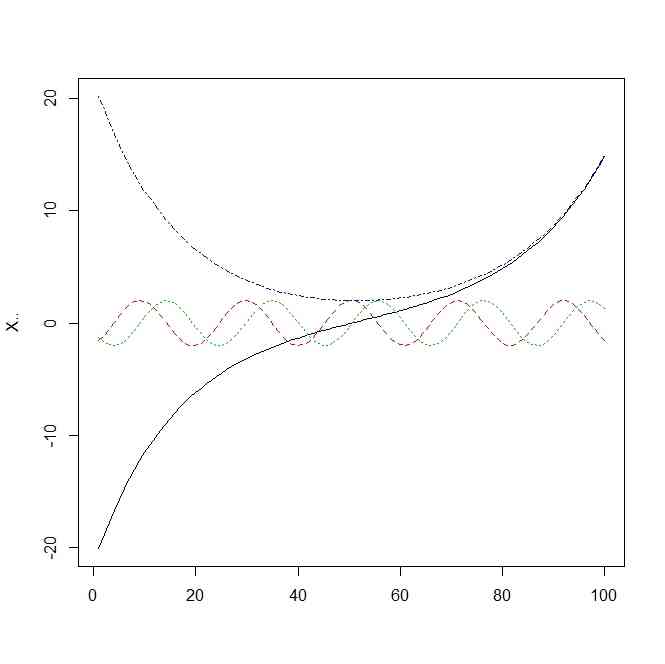
M <- matrix(c(1,-1,0,0,0,0,1,0,0,0,0,1,1,1,0,0),byrow=TRUE,4,4)
X.. <- t(M %*% t(X.))
matplot(X..,type="l")
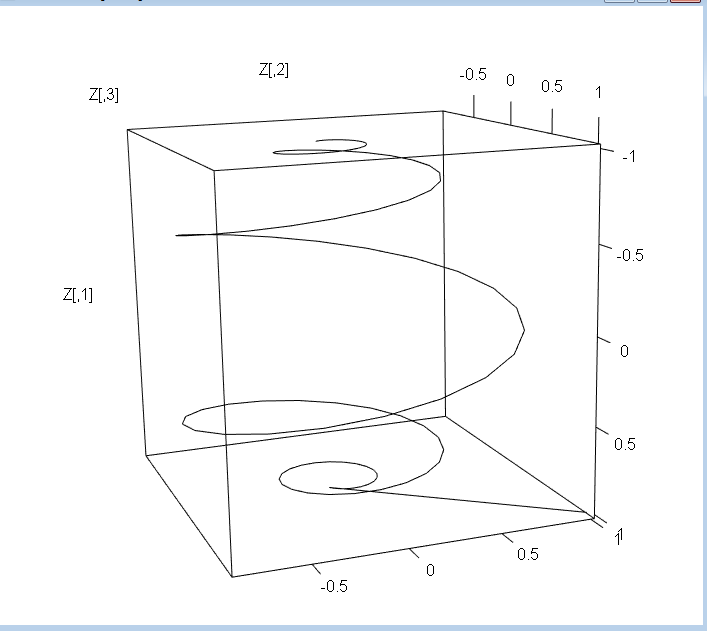
library(rgl)
Y <- X..[,1:3]/X..[,4]
Z <- rbind(Y,rep(min(Y),3))
Z <- rbind(Y,rep(max(Y),3))
plot3d(Z,type="l")
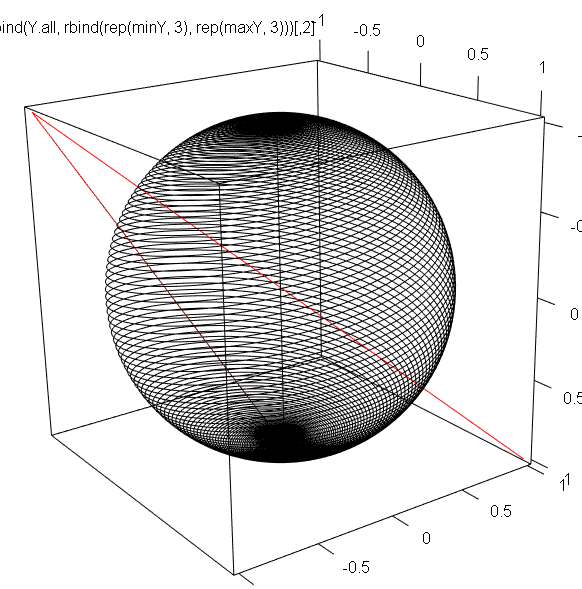
- 4次元空間で複数のらせんを作って、「円筒状」にした上で、3次元にした像を描いてみる
phis <- seq(from=0,to=1,length=30)*2*pi
Y.all <- matrix(0,0,3)
for(ii in 1:length(phis)){
Rot <- matrix(c(cos(phis[ii]),sin(phis[ii]),-sin(phis[ii]),cos(phis[ii])),2,2)
X.2 <- X.
X.2[,3:4] <- t(Rot %*% t(X.2[,3:4]))
X.. <- t(M %*% t(X.2))
Y <- X..[,1:3]/X..[,4]
Y.all <- rbind(Y.all,Y)
}
col <- rep(1,length(Y.all[,1]))
minY <- min(Y.all)
maxY <- max(Y.all)
plot3d(rbind(Y.all,rbind(rep(minY,3),rep(maxY,3))),col=c(col,rep(2,2)),type="l")
- 指数的らせん・対数らせんを射影して球が作れた
- パラメタをいじって、球を卵や栗に変化させてみる
x.init <- rep(1,4)
x.init[3:4] <- x.init[3:4]*k
-
-
- もう1つは、先すぼみの様子で、それは、指数関数的増加をする2軸の指数係数の比
- qは回転頻度を決める。面の形は変えず、面の上を巻き上がる曲線のピッチが変わる
d <- 0.75
lambdas <- c(d,-1,0+q*1i,0-q*1i )
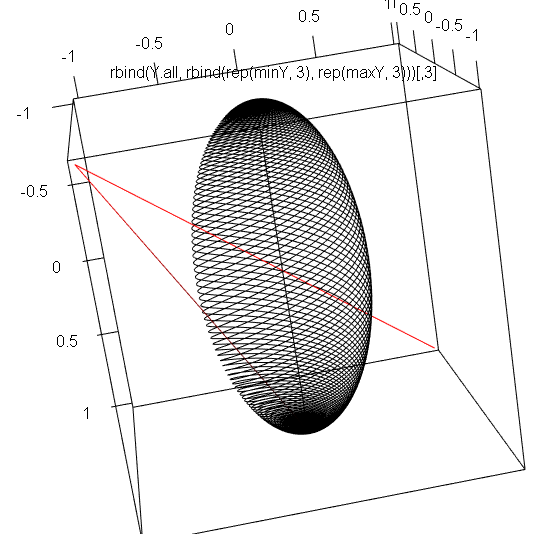
d <- 1
k <- 0.5
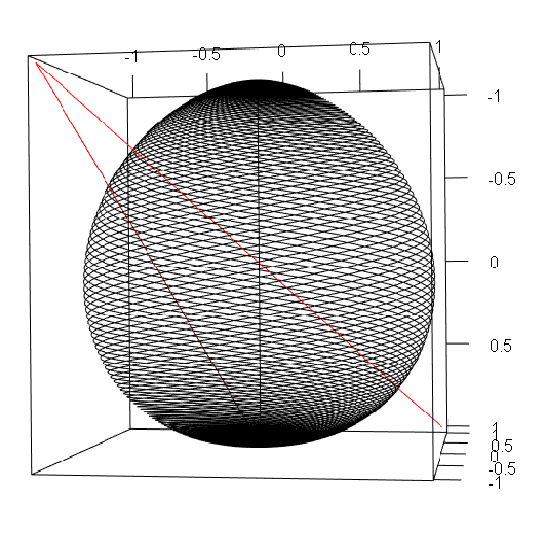
d <- 0.8
k <- 1
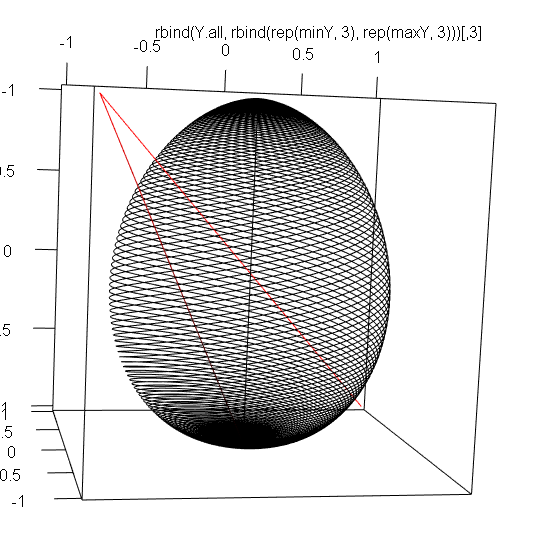
q <- 5
d <- 0.8
k <- 0.8
lambdas <- c(d,-1,0+q*1i,0-q*1i )
V <- matrix(c(1,0,0,0,0,1,0,0,0,0,1,-1i*1,0,0,1,1i*1),4,4)
M <- matrix(c(1,-1,0,0,0,0,1,0,0,0,0,1,1,1,0,0),byrow=TRUE,4,4)
x.init <- rep(1,4)
x.init[3:4] <- x.init[3:4]*k
t <- seq(from=-30,to=30,length=5000)
X <- matrix(0,length(t),4)
for(i in 1:4){
X[,i] <- x.init[i] * exp(lambdas[i]*t)
}
X. <- Re(t(V%*% t(X)))
phis <- seq(from=0,to=1,length=30)*2*pi
Y.all <- matrix(0,0,3)
for(ii in 1:length(phis)){
Rot <- matrix(c(cos(phis[ii]),sin(phis[ii]),-sin(phis[ii]),cos(phis[ii])),2,2)
X.2 <- X.
X.2[,3:4] <- t(Rot %*% t(X.2[,3:4]))
X.. <- t(M %*% t(X.2))
Y <- X..[,1:3]/X..[,4]
Y.all <- rbind(Y.all,Y)
}
col <- rep(1,length(Y.all[,1]))
minY <- min(Y.all)
maxY <- max(Y.all)
plot3d(rbind(Y.all,rbind(rep(minY,3),rep(maxY,3))),col=c(col,rep(2,2)),type="l")
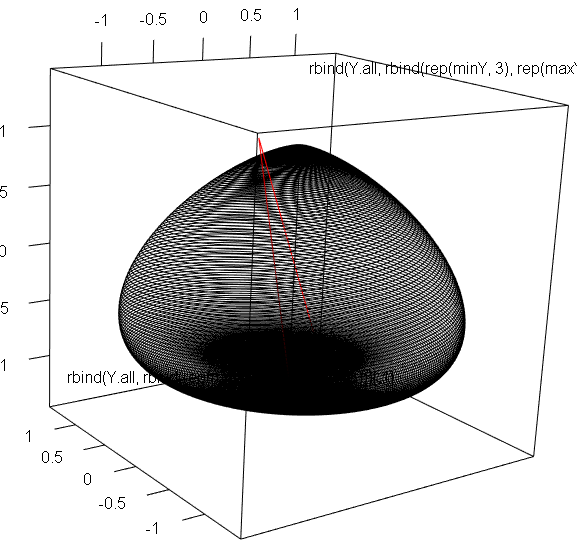
d <- 0.4
k <- 1.3







