遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

２つのベータ分布

ベータ分布 決断 R 不完全ベータ関数 正則ベータ関数 
a <-3
b <- 4
beta(a,b)
pbeta(0.3,a,b) # 正則ベータ関数(ベータ分布の累積密度関数)
pbeta(0.3,a,b) * beta(a,b) # 不完全ベータ関数(B(x=0.3;a=3,b=4)
  • ベータ分布
    • 真偽の事象で真偽がそれぞれa,b \ge 0回観測されたときの、真の生起確率pの分布としてベータ分布\frac{1}{B(a+1,b+1)}p^{a}(1-p)^bを共役事前分布としてとることがある
plot(dbeta(seq(from=0,to=1,length=100),a,b))

  • ２つの相互に独立なベータ分布の積(複合分布)
X <- matrix(c(3,4,7,9),2,2)
x <- seq(from=0,to=1,length=100)
p1 <- dbeta(x,X[1,1]+1,X[1,2]+1)
p2 <- dbeta(x,X[2,1]+1,X[2,2]+1)
p12 <- outer(p1,p2,"*")
image(p12,xlim=c(0,1),ylim=c(0,1))
par(new=TRUE)
contour(p12,add=TRUE)

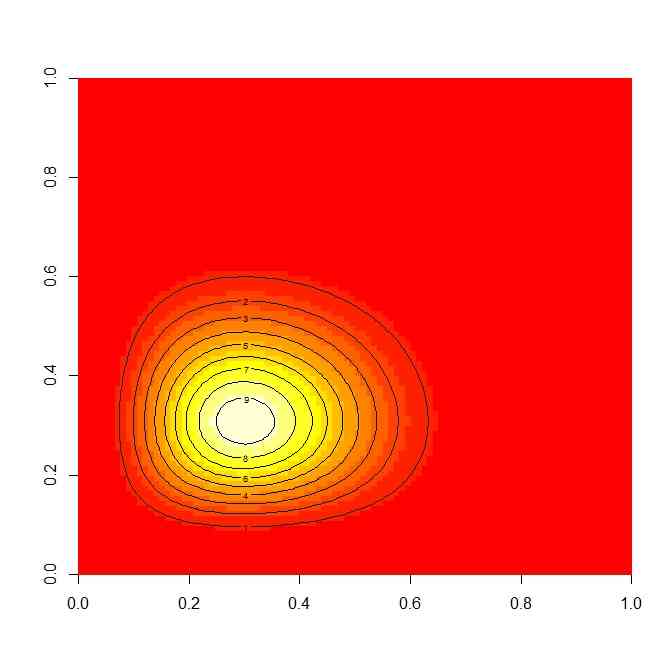
  • ２ベータ分布の勝敗分布
    • ここで２分布の勝負を考える
      • 片方の分布からの値が、もう片方の分布からの値より大きくなる確率は、この複合分布において、対角線の片側の部分の積分
abline(0,1)

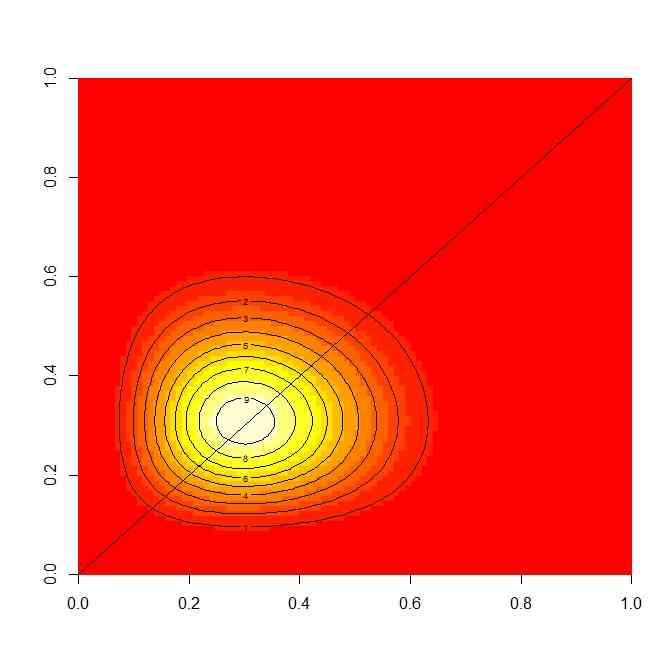
    • 式で表すと
    • P=\int_0^1 \int_0^ s f(s) g(t) dt ds
    • f(s)=\frac{s^{x-1}(1-s)^{y-1}}{B(x,y)}
    • g(t)=\frac{t^{z-1}(1-t)^{w-1}}{B(z,w)}
    • 上に記した、正則ベータ関数とかを使って、式変形していく
    • P=\int_0^1 f(s) I_s(z,w) ds
    • P=\int_0^1 f(s) \sum_{j=z}^{z+w-1} \begin{pmatrix}z+w-1\\j\end{pmatrix}s^j(1-s)^{z+w-1-j}ds
    • P=\int_0^1 \sum_{j=z}^{z+w-1}\frac{1}{B(x,y)} \begin{pmatrix}z+w-1\\j\end{pmatrix} s^{x-1+j}(1-s)^{y+z+w-2-j} ds
    • \int_0^1 x^{a-1} (1-x)^{b-1} dx = B(a,b)なので
    • P=\sum_{j=z}^{z+w-1}\frac{1}{B(x,y)}\begin{pmatrix}z+w-1\\j\end{pmatrix}B(x+j,y+z+w-1-j)
    • P=\sum_{j=z}^{z+w-1}\frac{1}{B(x,y)}\frac{1}{B(j+1,z+w-j)}\frac{1}{(z+w)}B(x+j,y+z+w-1-j)
  • Rで確かめてみよう
    • まずは、x,y,z,w４数を引数としてPを計算する関数を２つ
      • 式にべったりのそれと、\sum_jの影響の有無でまとめ直して、対数が取れるところは対数をとった２つを
    • 注。引数がx=(x1,x2,x3,x4)の場合とx=(x4,x3,x2,x1)の場合とは、複合確率密度関数の積分の仕方の軸を変更してはいるが、同じ積分なので値は同じ。x1,x4の大小が、\sum_{j}の項の数を決めているので、少ない方を採用するのが軽そうに思えるのでそうしておく
Decision_beta <- function(x){
	if(x[1] < x[4]){
		x <- x[4:1]
	}
	ret <- 0
	for(j in x[3]:(x[3]+x[4]-1)){
		ret <- ret + beta(x[1]+j,x[2]+x[3]+x[4]-1-j)/beta(j+1,x[3]+x[4]-j)/(x[3]+x[4])
	}
	return(ret/beta(x[1],x[2]))
}
Decision_beta.2 <- function(x){
	if(x[1] < x[4]){
		x <- x[4:1]
	}
	ret <- 0
	common <- -log(x[3]+x[4])+lgamma(x[1]+x[2])+lgamma(x[3]+x[4]+1)-lgamma(x[1])-lgamma(x[2])-lgamma(sum(x)-1)
	for(j in x[3]:(x[3]+x[4]-1)){
		tmp <- lgamma(x[1]+j)+lgamma(sum(x[2:4])-1-j)-lgamma(j+1)-lgamma(x[3]+x[4]-j)
		ret <- ret + exp(tmp+common)
	}
	return(ret)
}
    • ２つのベータ分布が真偽観測から作られることを考慮して、観測データを与えるバージョン。上の作りに合わせて異なる関数(結果は同じ)を３つ。Decision_Dice_beta.2.2()が一番よいだろう、多分。
Decision_Dice_beta.2 <- function(X){
	x <- X[1,1]
	y <- X[1,2]
	z <- X[2,1]
	w <- X[2,2]
	Decision_beta(c(x,y,z,w)+1)
}

Decision_Dice_beta.2.2 <- function(X){
	x <- X[1,1]
	y <- X[1,2]
	z <- X[2,1]
	w <- X[2,2]
	Decision_beta.2(c(x,y,z,w)+1)
}

Decision_Dice_beta <- function(X){
	x <- X[1,1]
	y <- X[1,2]
	z <- X[2,1]
	w <- X[2,2]
	ret <- 0
	for(j in (z+1):(z+w+1)){
		ret <- ret + beta(j+x+1,z+w+y-j+2)/beta(j+1,z+w+2-j)/(z+w+2)
	}
	return(ret/beta(x+1,y+1))
}
  • Stirlingの近似は、将来的に大きな値に対応する必要が出たときに入用なので、Wikiのベータ関数から引用しておく
    • B(x,y) \sim \sqrt{2\pi} \frac{x^{x-\frac{1}{2}}y^{y-\frac{1}{2}}}{(x+y)^{x+y-\frac{1}{2}}}