- 昨日、移動に際して格子を使って移動ベクトルの一致性を指標にする話を書いた
- 複雑な形に格子を正確に作るのは面倒なので、内部点を散在させてみることにする
- 本当はdelone setのようにばらばら加減が一定な点セットがよさそうだが、作成の手間が大きいようなので、普通の乱点くらいを想定する
- 平行移動・回転・歪みに対応してそれなりのマッチングを作ってくれるかもしれない
n.pt <- 100
t <- seq(from = 0, to = 1, length = n.pt) * 2 * pi
R <- rep(0,length(t))
ss <- rep(1,length(t))
s <- c(0,2*pi,runif(sample(3:8,1)) * 10-5)
for(j in 1:length(s)){
ss <- ss * (t-s[j])^2
}
R <- R + runif(1) * ss
t.2 <- c(t,t[1])
R.2 <- c(R,R[1])
R.2 <- (R.2 - min(R.2))/(max(R.2)-min(R.2))+1
plot(R.2*cos(t.2),R.2*sin(t.2),type="l")
R.3 <- R.2 * runif(length(R.2))^(1/2)
X <- rbind(cbind(R.2*cos(t.2),R.2*sin(t.2)),cbind(R.3*cos(t.2),R.3*sin(t.2)))
plot(X)
Y <- cbind(X[,1],X[,2])
theta <- pi/6
Rot <- matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),2,2)
Y <- Y %*% Rot
Y[,1] <- Y[,1]*1.2
Y[,2] <- Y[,2]*0.6
X <- X + rnorm(length(X),0,0.02)
Y <- Y + rnorm(length(Y),3,0.02)
Y <- (Y-min(Y)) + 3
Y[,1] <- (Y[,1]-min(Y[,1]))^1.2
out <- my.move(X,Y)
out.L <- my.move.L(X,Y)
xlim <- ylim <- range(c(X,Y))
par(mfcol=c(1,2))
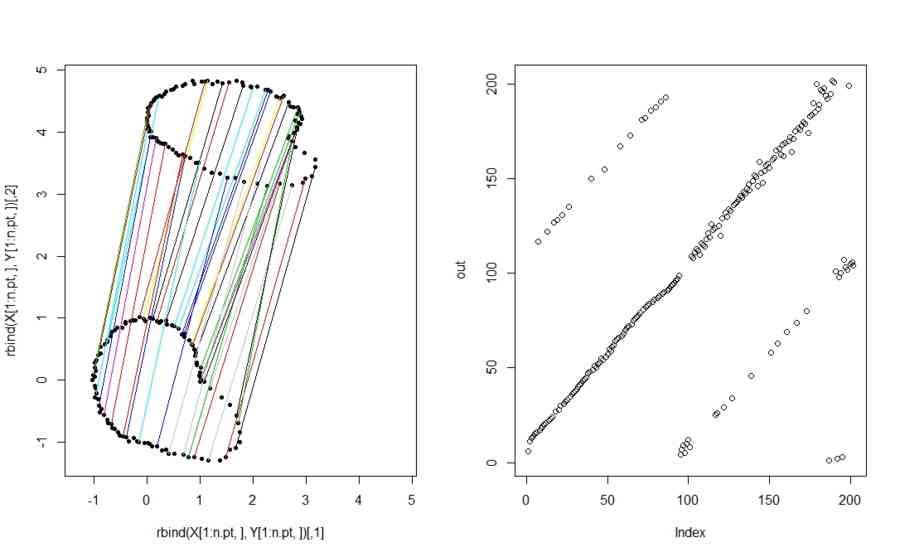
plot(rbind(X[1:n.pt,],Y[1:n.pt,]),pch=20,col=rep(1:2,each=length(X[,1])),xlim=xlim,ylim=ylim)
for(i in 1:n.pt){
if(runif(1)<0.4)
segments(X[i,1],X[i,2],Y[out[i],1],Y[out[i],2],col=sample(1:8,1))
}
plot(out)
par(mfcol=c(1,1))
