遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

Rで関数を自作する　Rでシミュレーションする、Rで関数を作る

R シミュレーション
  • A=(a1,a2,...)だったら、B=(b1,b2,...)を確率的にシミュレーションする、とは
  • B=(b1,b2,...)=f(A=(a1,a2,...)|P=(p1,p2,...))となるような変数P=(p1,p2,...)によって定まる関数f()を作り、その関数f()の内部でA=(a1,a2,...,)とP=(p1,p2,...)から乱数を使って演算をして、B=(b1,b2,...)を返させること
  • 関数を作る
# w=b*h^2
# 関数を作るには、function()という関数を使う
# my.fが作られる関数
my.f<-function(h,b=20){
# (h,b=20)により、この関数ではhとbという変数が
使われることがわかる
# hは値の指定がなく、bは20という値が指定されている
# 指定されていない変数は、使うときに指定する必要がある
# 指定されている変数は、使うときに値を指定しなければ、すでに指定されている値が使われる(デフォルト値)
# 指定されている変数は、使うときに値を指定しなおすこともできる
  w<-b*h^2 # この式は、与えた値から計算して出す過程
# 返却するときは、list()に納めて返す
# 計算した値(体重と、与えた値(身長とBIMインデックス)とを併せて返している
  return(list(weight=w,height=h,bmi.index=b))
}
  • 使ってみる
# 身長を与える
my.h<-1.7
# BMIインデックスはデフォルト値で体重を出してみる
my.w20<-my.f(h=my.h)
# BMIインデックスの値を変えて計算してみる
b2<-25
my.w25<-my.f(h=my.h,b=b2)
my.w20
my.w25

> my.w20
$weight
[1] 57.8

$height
[1] 1.7

$bmi.index
[1] 20

> my.w25
$weight
[1] 72.25

$height
[1] 1.7

$bmi.index
[1] 25
  • 何度か繰り返す、確率を入れる
    • AさんとBさんとが、ジャンケンの５回勝負をして、５回のうち何回勝つかを調べてみる
    • ただし、Aさん・Bさんともに、出し方に癖があって、グー・チョキ・パーを出す確率は、pa=(pa1,pa2,pa3),pb=(pb1,pb2,pb3)であるものとする
# グー・チョキ・パーを出す確率を与えて、実際にグー=1、チョキ=2、パー=3のどれかを出させる関数
gcp<-function(n=1,prob=c(1/3,1/3,1/3)){
  # 1,2,3からprobに応じて値をn個取り出して返す
  ret<-sample(1:3,n,replace=TRUE,prob=prob)
  return(ret)
}
# グー(1)、チョキ(2)、パー(3)の勝敗を行列で表してみる
# 勝ちは1、アイコは0、負けは-1
# 第１行はグーが、グー・チョキ・パーを相手にしたときの勝敗
# 第２行はチョキが、
# 第３行はパーが
M<-matrix(c(0,1,-1,-1,0,1,1,-1,0),byrow=TRUE,ncol=3)
M
# これを使ってジャンケン勝敗関数を作る
# a,bは1,2,3のいずれかの数で、グー・チョキ・パーに相当
# aがbに勝つかどうか
jyanken<-function(a,b){
  M<-matrix(c(0,1,-1,-1,0,1,1,-1,0),byrow=TRUE,ncol=3)
  return(M[a,b])
}
jyanken(1,2) # グーがチョキに勝つので1が返る
# N回繰り返してみる
# Aは少しグーを多く出しがち
pa<-c(10,11,11)
pa<-pa/sum(pa)
pa
# Bは少しパーを少なく出しがち
pb<-c(10,9,10)
pb<-pb/sum(pb)
pb
N<-1000
# 結果を格納するベクトル
T<-rep(0,N)
# 指定回数の繰り返しはfor(){}ループ
for(i in 1:N){
  # ５回勝負させる
  a<-gcp(n=5,prob=pa)
  b<-gcp(n=5,prob=pb)
  # ５回の勝負を判定する
  tmp<-c() # ５回分の勝ち負けを格納する
  for(j in 1:5){
    tmp<-c(tmp,jyanken(a[j],b[j]))
  }
  # Aが勝った回数(tmpの５個の値のうち、1であるものの個数)
  T[i]<-length(which(tmp==1))
}
# Aが５回勝負で勝つ回数(0,1,2,3,4,5のいずれか)
table(T)

> table(T)
T
  0   1   2   3   4   5 
115 349 339 152  43   2
  • BMIインデックスが20くらいの身長・体重データを適当に作る

# 身長は平均1.7mの正規分布で作る
# 肥満の集団を作るために、BMIインデックスは平均30の正規分布で与える
# 与えた身長とBMIインデックス値から体重を作ってやる
# 人数
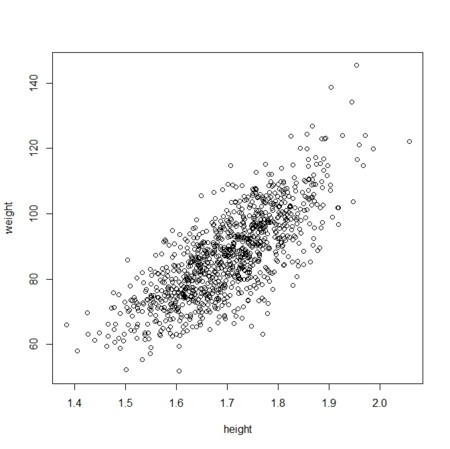
N<-1000
height.mean<-1.7
height.sd<-0.1
height<-rnorm(N,mean=height.mean,sd=height.sd)
bmi.mean<-30
bmi.sd<-3
bmi<-rnorm(N,mean=bmi.mean,sd=bmi.sd)
weight<-my.f(h=height,b=bmi)$weight
plot(height,weight)
  • どのくらい貯まるか
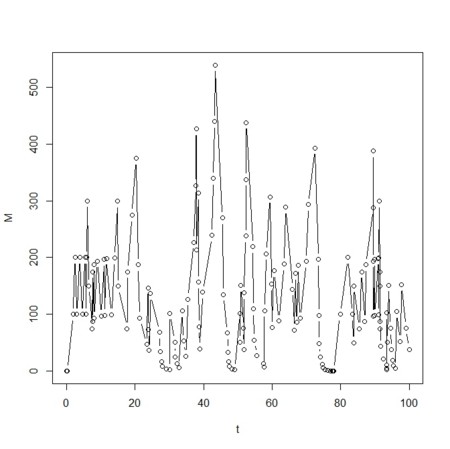
    • ときどきブラリと現れては、小遣いを100円、置いていくおじさんと、ときどきブラリと現れては、持っているお金の半分を奪い去っていく、もう一人のおじさんがいるときの、所有金額の推移をみてみよう
# 小遣いをくれるおじさんの単位時間あたりの平均来訪回数
p<-runif(1)
# 小遣いを奪っていくおじさんの単位時間あたりの平均来訪回数
q<-runif(1)
# 観察時間
T<-100
# それぞれの来訪間隔は指数分布に従う
# 観察時間Tに十分な来訪間隔を発生
Ps<-rexp(T/p*5,p)
Qs<-rexp(T/q*5,q)
# それぞれの来訪時刻は、来訪間隔の累積和
Ps2<-cumsum(Ps)
Qs2<-cumsum(Qs)
# ２人の来訪時刻を併せる
PQs2<-c(Ps2,Qs2)
# どちらが訪れたかを1,2でベクトルにする
PQs1<-c(rep(1,length(Ps2)),rep(2,length(Qs2)))
# 来訪時刻の昇順序
visit.order<-order(PQs2)
# 所有金額を記録
M<-c()
#　おじさん来訪時刻を記録
t<-c()
# 所有金額と時刻の初期値
current.money<-0
current.time<-0
counter<-0
# 来訪時刻が観察時刻より前である限り回すループ
while(current.time<T){
  # 所有金額・時刻を記録
  M<-c(M,current.money)
  t<-c(t,current.time)
  # 次の来訪について調べる
  counter<-counter+1
  # どちらのおじさんかを確認
  ojisan<-PQs1[visit.order[counter]]
  # 来訪時刻を確認
  current.time<-PQs2[visit.order[counter]]
  # おじさんによって所有金額の変化の仕方が変わる
  if(ojisan==1){
    current.money<-current.money+100
  }else if(ojisan==2){
    current.money<-current.money/2
  }
}
plot(t,M,type="b")


> p
[1] 0.703699
> q
[1] 0.8556833