必ず起きることは、いつまでに起きる？

• こちらでこんな計算をしている
  • 開始時点から、条件を満足するまでの時間を測っている
  • イベントが起きるまでの時間を測る
  • そのイベントは、開始時から一定期間内に必ず１度起きるようなイベントで、いつおきるかはランダムだという
  • イベントが観察されたら、その瞬間から、また次のイベントが同じ条件で起きることになっているので、また次のイベントまでの時間を測る
  • 累積した時間が一定時間に達するのは、何度目のイベントが起きたときか
• ランダムに起きるイベントの間隔を測っているようなので、指数分布とかポアッソン分布とかに似ているけれど、「ある期間内に必ず起きる」という条件が違うようだ
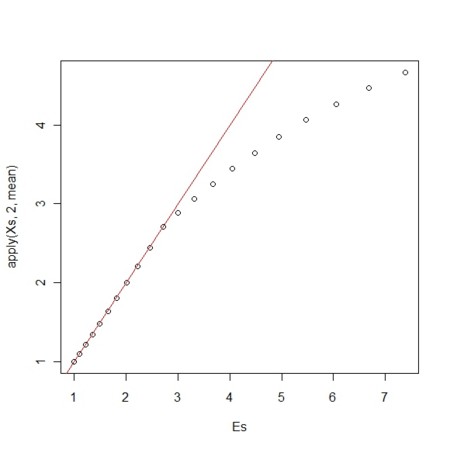
• 時間が1までは平均回数は「(ちょっと)指数関数風」に増えて、そこで折れ曲がって、直線状に増えるようになる？？？

# 一様乱数行列を作る
Niter<-10000
Ncol<-50
M<-matrix(runif(Niter*Ncol),ncol=Ncol)
# 累積時間を取る
M2<-apply(M,1,cumsum)

#matplot(M2,type="l")
# 累積時間がどれくらいになったときを問題にするのか
# その時刻をいろいろにふる
Ts<-seq(from=0,to=2,by=0.1)
# その回数を記録する
Xs<-matrix(0,length(M2[1,]),length(Ts))
for(i in 1:length(M2[1,])){
	for(j in 1:length(Ts)){
		Xs[i,j]<-length(which(M2[,i]<Ts[j]))+1
	}
	
}
# ふった時刻ごとに、「何回目」かの平均をプロットする
plot(Ts,apply(Xs,2,mean),type="l")
Es<-exp(Ts)
plot(Es,apply(Xs,2,mean))
abline(0,1,col=2)